Das Weltraumteleskop Kepler ist eigentlich dazu da, um Exoplaneten zu entdecken. Und das macht es auch ziemlich gut. Aber wenn man lang genug ins Universum schaut, findet man auch andere Sachen. Ich habe schon über Keplers Suche nach Dreifachsternen berichtet – und jetzt haben die Kepler-Wissenschaftler noch etwas anderes sehr schönes und interessantes gefunden.
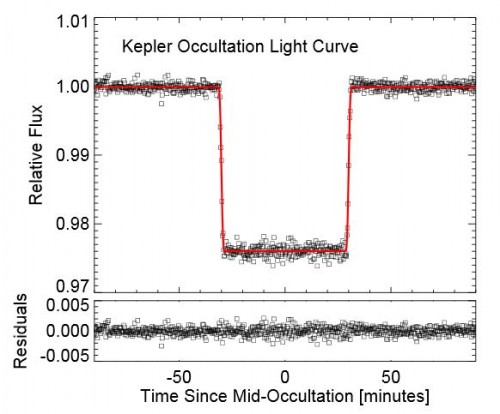
Philip Muirhead und seine Kollegen haben das Kepler Object of Interest 256 (KOI-256) untersucht. Dieser Stern sah zuerst genau so aus, wie die Sterne, die man finden wollte. Kepler sucht ja nach Sternen, deren Licht in regelmäßigen Abständen ein wenig dunkler wird. Das ist ein Zeichen, dass diese Sterne von Planeten umkreist werden. Denn jedesmal wenn der Planet von uns aus gesehen vor dem Stern steht, blockiert er ein wenig von dessen Licht. Und genau das hat man bei KOI-256 beobachtet:
Man sieht in diesem Bild sehr schön, wie die Helligkeit des Sterns schnell abfällt und dann wieder ansteigt. Aus dieser Lichtkurve erhält man aber nur Informationen darüber, wie groß das verdunkelnde Objekt ist und leider nichts darüber, wie schwer es ist. Um das herauszufinden haben die Astronomen um Muirhead den Stern nochmal vom Erdboden aus beobachtet. Mit dem Hale-Teleskop der Palomar-Sternwarte haben sie nachgesehen, wie stark der Stern hin und her wackelt. Denn ein Planet verdunkelt das Licht des Sterns nicht nur; seine Gravitationskraft führt auch dazu, dass der Stern sich ein klein wenig hin und her bewegt. Und die Stärke dieser Bewegung hängt von der Masse des Planeten ab.
Muirhead und seine Kollegen waren sehr überrascht, als sie merkten, dass KOI-256 ziemlich stark wackelte. Viel stärker, als es ein normaler Planet verursachen kann. Das Wackeln deutete eher auf einen zweiten Stern hin. Aber wenn sich zwei Sterne umkreisen, dann müsste der Helligkeitsabfall viel größer sein. Denn wenn sich zwei Sterne umkreisen, dann sieht man viel ausgeprägtere Lichtkurven. Man bekommt entweder das Licht von zwei Sternen zu sehen oder nur das Licht von einem Stern (wenn einer gerade hinter dem anderen steht). Das war bei KOI-256 aber nicht der Fall. Die Lichtkurve deutete auf ein kleines Objekt hin, das nur einen winzigen Bruchteil der Sternenfläche bedeckt. Die Messung des Wackelns aber zeigte, dass es sich um ein Objekt handeln muss, das so schwer wie ein ganzer Stern. KOI-256 wird also offensichtlich von einem sehr kleinen aber sehr schweren Objekt umkreist. Es handelt sich nicht um einen Planeten, sondern um einen weißen Zwerg!
Ein weißer Zwerg ist das, was von einem sonnenähnlichen Stern übrig bleibt, wenn der am Ende seines Lebens keinen Brennstoff mehr übrig hat. Zuerst pustet so ein Stern seine äußeren Atmosphärenschichten ins All bis dann nur noch der enorm dichte Kern übrig bleibt. Ein weißer Zwerg wiegt immer noch fast so viel wie ein ausgewachsener Stern; ist aber nur so groß wie die Erde.
Das alleine wäre schon eine schöne Entdeckung gewesen. Muirhead und seine Kollegen haben aber noch etwas entdeckt. Denn die Sache mit der Lichtkurve war ein klein wenig komplizierter, als es auf den ersten Blick aussah. Die Kurve, die ihr weiter oben sehen könnt, zeigt die Situation die auftritt, wenn der weiße Zwerg hinter dem Stern steht. Da der weiße Zwerg auch selbst leuchtet, wird es ein wenig dunkler, wenn sein Licht vom Stern blockiert wird. Man hat natürlich auch gemessen, was passiert, wenn der weiße Zwerg vor dem Stern steht. Auch da sollte das Licht ein wenig schwächer werden, weil ja nun der Zwerg Licht des Sterns blockiert und selbst aber nicht hell genug strahlt, um das auszugleichen. Aber die Messungen zeigten, dass das Licht nicht ganz so stark abfiel, wie man es eigentlich erwartet hatte.











Kommentare (25)