Die meisten astronomischen Prozesse spielen sich auf Zeitskalen ab, die viel zu lang für unsere menschlichen Maßstäbe sind. Es dauert Millionen Jahre, bis ein Planet entstanden ist; will man zwei Galaxien bei der Kollision zusehen dauert das Milliarden Jahre und selbst die vergleichsweise kurzfristigen Änderungen in planetaren Orbits finden im Laufe von Jahrhunderten und Jahrtausenden statt. Die Astronomen können daher selten einen kompletten Prozess beobachten sondern müssen sich das komplette Bild zusammen puzzlen. Anstatt einer galaktischen Kollision von Anfang bis zum Ende zuzusehen sucht man sich zwei Galaxien, die gerade am Anfang einer Kollision stehen; zwei andere Galaxien die gerade mitten drin sind und wieder zwei andere Galaxien, bei denen alles schon vorbei ist und probiert daraus ein komplettes Bild des Vorgangs abzuleiten. Das ist ein mühsamer Prozess, aber anders geht es eben nicht. Und selbst wenn es manchmal die Möglichkeit gäbe, irgendwo zuzusehen, verpasst man es trotzdem. Denn das Universum ist groß und man weiß selten im voraus, wann und wo es etwas Lohnendes zu sehen gibt. Vier Astronomen aus Paris haben sich über dieses Problem Gedanken gemacht. Sie wollen beobachten, wie Asteroiden gefährlich werden.
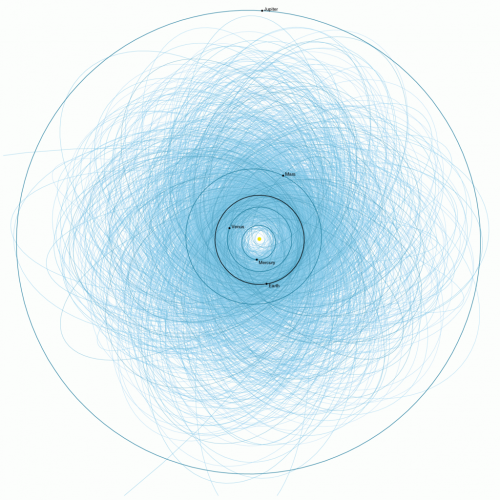
Bahnen potentiell gefährlicher Asteroiden (Bild: JPL/NASA)
Die meisten Asteroiden in unserem Sonnensystem tun uns nichts. Sie ziehen friedlich ihre Bahnen um die Sonne; die eine Gruppe zwischen den Orbits von Mars und Jupiter und die anderen noch weiter draußen hinter der Bahn des Neptuns. Für die Erde gefährlich sind beide Gruppen nicht. Wir müssen uns um die erdnahen Asteroiden Sorgen machen. Das sind Himmelskörper, die sich zwischen den Bahnen von Venus und Mars aufhalten und die Bahn der Erde kreuzen können. Das birgt das Potential für eine Kollision – aber es zeigt uns auch, dass diese Gruppe von Asteroiden nicht langfristig stabil sein kann. Asteroiden die immer wieder in die Nähe von Planeten (in diesem Fall Venus, Erde und Mars) kommen, erfahren auch jede Menge gravitative Störungen. Ihre Bahnen ändern sich ständig; sie sind chaotisch und irgendwann fliegen sie aus dem Sonnensystem raus oder kollidieren mit einem der Planeten bzw. der Sonne. Die Lebenszeit eines typischen erdnahen Asteroiden liegt zwischen ein paar zehntausend und ein paar hunderttausende Jahren. Verglichen mit dem Alter des Sonnensystems von 4,5 Milliarden Jahren ist das fast nichts und wenn wir heute immer noch erdnahe Asteroiden beobachten, dann muss es einen Prozess geben, der immer wieder neue Asteroiden dieser Gruppe erzeugt.
Wie dieser Prozess aussieht, ist bekannt. Asteroiden die sich im Hauptgürtel zwischen den Bahnen von Mars und Jupiter befinden, bleiben dort normalerweise auch. Manche von ihnen können aber durch verschiedene Effekte in ganz spezielle Bereiche geschubst werden. Zum Beispiel wenn zwei Asteroiden zusammenstoßen, was ab und zu mal vorkommen kann. Dann können Bruchstücke in sogenannten resonanten Bereichen landen. Was “Resonanzen” in diesem Zusammenhang sind, habe ich hier ausführlich erklärt. Von einer Resonanz spricht man immer dann, wenn die Änderung eines Bahnparameters eines Himmelskörpers in einem ganzzahligen Verhältnis zur Änderung des gleichen Parameters eines anderen Himmelskörpers steht. Der einfachste Fall betrifft die Umlaufzeit: Wenn ein Himmelskörper zum Beispiel genau doppelt so lange für eine Umkreisung braucht als ein anderer Himmelskörper, dann spricht man von einer 2:1 Resonanz der mittleren Bewegung. Schafft der eine fünf Umläufe während der andere zwei macht, dann ist es eine 5:2 Resonanz. Und so weiter. Neben diesen Resonanzen der mittleren Bewegung bzw. “mean-motion resonances (MMR)” gibt es auch noch säkulare Resonanzen. Hier stehen nicht die Umlaufzeiten der Himmelskörper in einem ganzzahligen Verhältnis, sondern die Perioden mit denen sich die Bahnen im Laufe der Zeit verändern. Die Störungen der Planeten führen ja dazu, dass ein Himmelskörper nicht ständig auf der immer gleichen Bahn um die Sonne läuft sondern sich die Bahn im laufe der Zeit langsam ändert. Die Bahn kann zum Beispiel im Raum hin und her kippen. Und wenn nun eine Planetenbahn genau zweimal hin und her wackelt während die andere einmal hin und her wackelt, dann spricht man von einer säkularen Resonanz.
MMRs und sekulare Resonanzen können zu verstärkten gravitativen Störungen führen. Die Störungen, die sich normalerweise gegenseitig ausgleichen würden, können in einer resonanten Position verstärkt werden und die Bahn eines Himmelskörpers deutlich verändern. Landet nun ein Asteroid in so einer resonanten Position, dann kann er durch die Störungen (im Allgemeinen ist dann Jupiter verantwortlich) seine Bahn so stark verändern, dass er irgendwann bei den erdnahen Asteroiden landet. Die Resonanzen sind es also, die immer wieder für Nachschub bei den potentiell gefährlichen Himmelskörpern sorgt.
Dieser Prozess ist schon lange bekannt und auch in Computersimulationen sehr, sehr oft untersucht worden. Aber meines Wissens nach hat man noch nie beobachtet wie ein Asteroid aus einer resonanten Position heraus zum erdnahen Asteroid wurde. Das passiert natürlich auch nicht von heute auf morgen sondern kann Jahrzehnte oder Jahrhunderte dauern. Aber mit den mittlerweile sehr genau möglichen Positionsmessungen könnte man das durchaus schon frühzeitig erkennen. Wenn man denn wüsste, wo man hinsehen muss…
Und genau das haben Anatoliy Ivantsov und seine Kollegen von der Pariser Sternwarte untersucht. In einem kurzen Konferenzbeitrag mit dem Titel “On future opportunities to observe gravitational scattering of main belt asteroids into NEO source regions” haben sie Computersimulationen angestellt um herauszufinden, bei welchen Asteroiden die größte Chance besteht, dass sie in naher Zukunft aus einer resonanten Position hinaus zu erdnahen Asteroiden werden. Insgesamt wurden 1335 Asteroiden untersucht. 52 davon befanden sich in der Nähe der 3:1, 5:2, 2:1 oder 7:3 MMR mit Jupiter und 1273 Asteroiden waren in der Nähe verschiedener säkularer Resonanzen. Am Ende zeigte sich, dass jeweils knapp 10 Prozent Potential haben, von der Resonanz ausreichend gestört zu werden um sich zu erdnahen Asteroiden zu entwickeln. Jetzt muss da nur noch jemand lang genug hin sehen…
(P.S. Falls jemand ganz konkrete Fragen zum angesprochenen Fachartikel haben sollte: Einer der Autoren hat früher in Wien gemeinsam mit mir in der gleichen Arbeitsgruppe gearbeitet und ich kann ihn sicher dazu überreden hier aufzutauchen und die eine oder andere Frage zu beantworten)











Kommentare (54)