Wie bewegen sich Himmelskörper? Und wie kann man ihre Bewegung vorhersagen? Das Problem ist Jahrtausende alt und ebenso lange sucht man nach einer Lösung. Selbst wenn nur drei Himmelskörper beteiligt sind, ist die Frage erstaunlich schwer zu beantworten. WIE schwer die Antwort zu finden ist und wieso die Sache so kompliziert ist, erfahrt ihr in der neuen Folge der Sternengeschichten.
Und wie immer gibt es weiter unten eine Transkription des Podcasts.
Die Folge könnt ihr euch hier direkt als YouTube-Video ansehen oder direkt runterladen.
Den Podcast könnt ihr unter
abonnieren beziehungsweise auch bei Bitlove via Torrent beziehen.
Am einfachsten ist es, wenn ihr euch die “Sternengeschichten-App” fürs Handy runterladet und den Podcast damit anhört.
Die Sternengeschichten gibts natürlich auch bei iTunes (wo ich mich immer über Rezensionen und Bewertungen freue) und alle Infos und Links zu den vergangenen Folgen findet ihr unter https://www.sternengeschichten.org.
Und natürlich gibt es die Sternengeschichten auch bei Facebook und bei Twitter.
Transkription
Sternengeschichten Folge 175: Das Dreikörperproblem
Das Dreikörperproblem sucht nach einer Antwort auf eine der fundamentalen Fragen der Astronomie: Wie bewegen sich Himmelskörper und vor allem: Wie kann man diese Bewegung voraussagen. Das war schon wichtig für die Menschen, lange bevor es die Astronomie als echte Naturwissenschaft gab. Man wollte wissen, wie sich Sonne und Mond über den Himmel bewegen um einen Überblick über den Kalender und die richtigen Zeiten für Aussaat und Ernte zu haben. Man wollte die religiösen Feste zu den richtigen Zeiten feiern und natürlich existierte damals auch noch die Vorstellung, dass die Himmelskörper Manifestationen der Götter seien und ihre Bewegung uns etwas über unsere Zukunft sagen könne.
Noch simpel: Das Zweikörperproblem (Bild: Public Domain)
Innerhalb gewisser Grenzen ist es möglich, Vorhersagen über die Bewegung der Himmelskörper zu machen, auch wenn man keine Vorstellungen über die physikalisch-astronomischen Grundlagen dieser Bewegung hat. Der Bewegung der Planeten erfolgt näherungsweise periodisch und wenn man nur lange genug Daten sammelt, kann man solche Perioden erkennen und zur Vorhersage nutzen.
Das hat funktioniert, aber nicht sehr genau. Unter anderem, weil man nicht wusste, dass die Erde selbst ein Planet ist, der sich bewegt und diese Bewegung die Beobachtung der Bewegung der anderen Planeten kompliziert macht. Und auch, weil die Bewegung eben nur annähernd periodisch ist. Planeten bewegen sich nicht auf exakten Kreisbahnen und immer gleich schnell, sondern auf elliptischen Bahnen und zu unterschiedlichen Zeiten mit unterschiedlichen Geschwindigkeiten.
Der erste, der eine einigermaßen brauchbare Vorstellung von der Bewegung der Himmelskörper hatte, war Johannes Kepler im 17. Jahrhundert. Mit seinen Keplerschen Gesetzen zur Planetenbewegung konnte er viel besser vorhersagen, wie sich die Himmelskörper bewegen als alle seine Vorgänger. Das, was Keplers Gesetze beschreiben ist aber genaugenommen nur ein “Zweikörperproblem”.
Man kann damit erklären was passiert, wenn EIN Planet EINEN Stern umkreist. In unserem Sonnensystem ist das aber nicht der Fall. Hier gibt es acht Planeten und dazu jede Menge Monde, Asteroiden und Kometen. Und, das wusste man seit der revolutionären Arbeit von Isaac Newton, JEDES Objekt beeinflusst jedes andere mit seiner Gravitationskraft. Will man also wirklich genau wissen, wie sich ein Himmelskörper bewegt, dann darf man nicht nur schauen, was zwischen ihm und der Sonne abspielt. Man muss genaugenommen den gravitativen Einfluss aller Himmelskörper berücksichtigen.
Aber das sollte ja eigentlich kein Problem sein. Immerhin hat Isaac Newton ja nicht nur erkannt, dass die Gravitation universal ist und zwischen allen Himmelskörpern wirkt. Sondern auch mathematische Gleichungen gefunden, mit denen sich der Gravitationseinfluss beschreiben lässt.
Und es ist tatsächlich nicht allzu schwer, entsprechende Gleichungen zu formulieren, die die Bewegung zum Beispiel der Erde unter dem Einfluss aller anderen Planeten des Sonnensystems beschreiben. Die Gleichungen aufzuschreiben ist aber nur der erste Schritt. Als nächstes muss man sie aber auch noch lösen!
Beim Zweikörperproblem ist das leicht möglich. Betrachtet man nur die Sonne und einen Planeten und löst die Gleichungen die aus Newtons Theorie folgen, dann erhält man exakt die Gesetze, die auch schon Kepler gefunden hat. Sobald man aber einen dritten Körper mit ins Spiel bringt, wird die Sache nicht nur schwieriger sondern nahezu unmöglich!
Rein intuitiv kann man auch verstehen, warum das so ist. Stellen wir uns die Erde, die Sonne und zum Beispiel den Mars vor. Die Sonne hat von allen die größte Masse und daher auch den größten gravitativen Einfluss. Deswegen bewegen sich auch Mars und Erde um die Sonne herum. In erster Näherung kann man dieses Dreikörperproblem als zwei Zweikörperprobleme betrachten. Die Gravitationskraft der Sonne führt dazu, dass sich die Erde in einer leicht elliptischen Bahn um sie herum bewegt. Und die Gravitationskraft der Sonne führt dazu, dass sich der Mars in einer leicht elliptischen Bahn um sie herum bewegt. Natürlich üben sowohl der Mars als auch die Erde gravitative Störungen auf die Sonne aus. Aber weil die Masse der Planeten im Vergleich zur Sonnenmasse so gering ist, passiert da nicht viel. Die Sonne wackelt ein ganz kleines bisschen, aber mehr geschieht da nicht.
Verlässt man die Näherung und betrachtet die gesamte Situation, wird es schnell kompliziert. Wie genau die Bahn der Erde um die Sonne aussieht, hängt unter anderem vom Abstand zwischen den beiden Himmelskörpern aus. Aber die Erde wird im Dreikörperproblem ja auch vom Mars beeinflusst. Dieser Einfluss ist zwar klein, aber vorhanden. Der Mars sorgt also dafür, dass sich der Abstand zwischen Erde und Sonne ein klein wenig ändert. Damit ändert sich aber auch die Stärke der Anziehungskraft zwischen Sonne und Erde. Und damit auch die Bahn der Erde um die Sonne. Das aber wiederum führt zu einer Veränderung in der Anziehungskraft zwischen Erde und Mars; zu einem veränderten Abstand zwischen Sonne und Erde, und so weiter. Und das gleiche gilt natürlich auch umgekehrt für den Einfluss der Erde auf den Mars.
Es ist eine unendliche Reihe von gegenseitiger Beeinflussung bei der absolut nicht klar ist, wie man die Sache auflösen soll. Die intuitive Schwierigkeit beim Verständnis der wechselseitigen Beeinflussung von drei Himmelskörpern spiegelt sich auch in ganz konkreten mathematischen Schwierigkeiten wieder die auftreten, wenn man versucht die entsprechenden Gleichungen zu lösen.
Auf diese Details will ich gar nicht näher eingehen – vielleicht gibt es dazu mal eine eigene Folge der Sternengeschichten. Jedenfalls ist es den Wissenschaftlern nicht gelungen, das Dreikörperproblem mathematisch zu lösen. Man hat es lange genug probiert. Wie ich in Folge 96 der Sternengeschichten erzählt habe, wurde für die Beantwortung dieser Frage im 19. Jahrhundert sogar ein Preis ausgesetzt und der große Mathematiker Henri Poincaré hat probiert, ihn zu gewinnen. Er fand ebenfalls keine Lösung – aber er fand heraus, dass es mathematisch unmöglich ist, das Dreikörperproblem zu lösen! Gleichzeitig mit dieser Erkenntnis entwickelte er die Grundlagen der Chaostheorie. Seitdem wissen wir, dass bestimmte dynamische Systeme so komplex sind, dass sie mit klassischen Methoden nicht vorhersagbar sind. Und unser Sonnensystem gehört dazu.
Heute verwendet man Computersimulationen um die Bewegung von Himmelskörpern vorherzusagen, wie ich in Folge 9 der Sternengeschichten ausführlicher erklärt habe. Aber trotzdem haben die Wissenschaftler nicht aufgehört, sich Gedanken über das Dreikörperproblem zu machen. Sie haben einerseits verschiedene Variationen dieses Problems entwickelt, die zwar die Realität nicht mehr ganz exakt beschreiben aber doch noch so gut, um innerhalb gewisser Grenzen brauchbare Vorhersagen machen zu können. Lösungen für solche “eingeschränkte Dreikörperprobleme” wurden im Laufe der Zeit gefunden; zum Beispiel in Form der Lagrangepunkte, die ich in Folge 31 der Sternengeschichten beschrieben habe.
Interessanterweise ist es dann sogar doch noch gelungen, das Dreikörperproblem selbst zu lösen. So irgendwie zumindest…
Das, was das Dreikörperproblem unter anderem so schwierig macht, sind nahe Begegnungen oder gar Kollisionen zwischen Himmelskörpern. Je näher sich zwei Objekte kommen, desto stärker wird die Gravitationskraft zwischen ihnen. Und desto größer werden auch die Probleme, die ich vorhin beschrieben habe. Aus mathematischer Sicht wird die Gravitationskraft unendlich groß, wenn der Abstand zweier Himmelskörper bei einer Kollision gleich null wird. In den Gleichungen taucht dort dann eine Division durch Null auf und damit hat die Mathematik ja generell ein Problem.
Im Jahr 1912 hat der finnische Mathematiker Karl Frithiof Sundman aber eine Lösung gefunden. Beziehungsweise so etwas ähnliches wie eine Lösung. Er konnte eine Lösung für die Gleichungen des Dreikörperproblems angeben, aber nur in Form einer sogenannten unendlichen Reihe. Also einer Summe die aus unendlichen vielen Zahlen gebildet wird. Das ist nicht so seltsam wie es klingt. Wenn man zum Beispiel berechnen will, wie viel 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + usw. ist, dann kann man diese Reihe unendlich lange fortsetzen. Aber jede Zahl in dieser Summe ist kleiner als die vorherige. Die Summe aller Zahlen wächst also, aber nicht immer weiter und weiter. Sie nähert sich einem ganz bestimmten Wert und mit den richtigen mathematischen Methoden kann man zeigen, dass die Summe all dieser unendlich vielen Zahlen nicht selbst unendlich ist, sondern in diesem Fall gleich zwei.
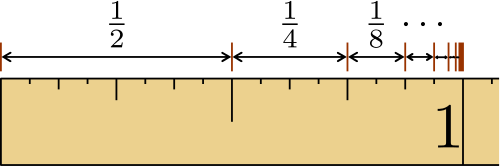
Unendliche viele Zahlen und trotzdem eine endliche Summe… (Bild: Gemeinfrei)
So eine Lösung hat auch Sundman gefunden für das Dreikörperproblem gefunden. Er hat gezeigt, dass auch hier eine Reihe unendlich vieler Zahlen existiert, die sich am Ende nicht zu unendlich aufaddieren sondern eben zur Lösung der Gleichung. Aber. Und das ist ein großes “Aber”! Aber richtig viel anfangen kann man mit der Lösung nicht. Sundmans Technik funktioniert nur, wenn man von Anfang an voraussetzt, das Himmelskörper nicht miteinander kollidieren dürfen. Das ist aber in der Realität nicht der Fall. Aber selbst wenn man das ignoriert, kommt man mit seiner Lösung nicht weit. Es gibt keinen einfachen Weg, die unendlichen vielen Zahlen in Sundmans Summe aufzuaddieren. Und man kann nicht einfach zwischendurch aufhören und sich sagen: Ach, das reicht jetzt schon – es muss ja nicht absolut genau sein, sondern nur ausreichend genau um gute Vorhersagen zu machen. Beziehungsweise man kann das schon sagen. Aber um ausreichend gute Vorhersagen machen zu können, müsste man absurd viele Zahlen addieren. Die Zahl der nötigen Einträge in Sundmans Summe wäre eine 1, gefolgt von 8 Millionen Nullen!
Sundmans Lösung des Dreikörperproblems ist also zwar nett und mathematisch interessant. Aber in der Praxis auch völlig unbrauchbar. Das Dreikörperproblem bleibt ungelöst.












Kommentare (13)