Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2016. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier.

Das sagt die Autorin des Artikels, Ann-Cathrin über sich:
Keine Angabe
——————————————
HIGGS – Was ist das und warum ist das so wichtig?
Im Jahr 2012 wurde am Teilchenbeschleuniger LHC das Higgs-Boson nachgewiesen. Dafür erhielten im Jahr 2013 zwei Wissenschaftler den Nobelpreis im Fach Physik. Für die Teilchenphysik war diese Entdeckung eine Sensation. Denn bereits im Jahr 1964 wurde dieses besondere Teilchen vorausgesagt.
In meinem Artikel werde ich erklären, was so besonders an diesem Teilchen ist und warum es deshalb auch so wichtig ist. Denn erst mit dem Beweis des Higgs-Bosons konnte sich die Frage „Woher kommt die Masse?“ klären lassen. Hinter dem Teilchen steckt ein Mechanismus, der nämlich dafür sorgt, dass alle Teilchen, die Masse besitzen, auch Masse bekommen. Man kann sich ja schlecht eine Welt ohne jegliche Masse vorstellen.
Aber was genau ist das Higgs-Boson eigentlich. Da viele Menschen sich eher weniger mit Teilchenphysik auskennen, wird mit dem Higgs-Boson meistens Schluckauf oder ähnliches assoziiert, anstatt dass man an ein Elementarteilchen denkt. Zuerst einmal zu den Eigenschaften dieses Teilchens. Es ist wie bereits erwähnt ein Elementarteilchen und lässt sich innerhalb des Standardmodells den Bosonen zuordnen.
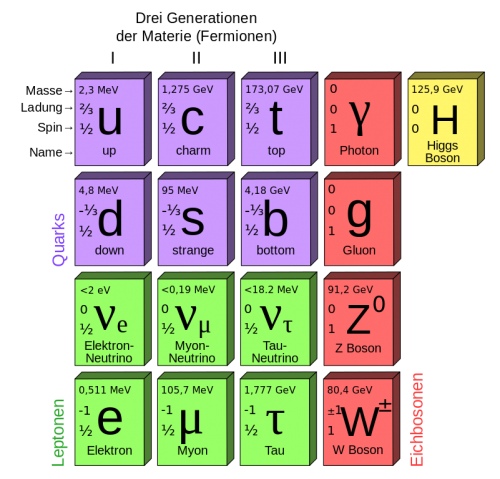
Das Standardmodell der Elementarteilchenphysik (Bild: Polluks (Standard_Model_of_Elementary_Particles.svg, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=11307906)
Es hat eine Masse von ungefähr 125000 MeV/c2. Besonders am Higgs-Boson ist, dass es einen Spin 0 hat. Das bedeutet, dass es sich nicht dreht, wobei alle anderen Teilchen aus dem Standardmodell einen bestimmten Spin haben und sich somit auch drehen. Die mittlere Lebensdauer des Higgs-Bosons beträgt 10-22 Sekunden. Auf Grund dieser kurzen Lebensdauer war es auch so extrem schwierig es nachzuweisen. Denn in dieser winzigen Zeitspanne lässt sich mit keinem Gerät dieser Welt ein Teilchen nachweisen. Daher musste man auch die verschiedenen möglichen Zerfallsprodukte des Higgs-Bosons untersuchen, um jenes nachzuweisen.

Simulation des Zerfalls eines Higgs-Teilchens am Cern (Bild: Lucas Taylor / CERN – https://cdsweb.cern.ch/record/628469, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=1433671)
Jedes Elementarteilchen unterliegt einer Wechselwirkung, auch das Higgs-Teilchen. Dieses unterliegt nämlich der schwachen Wechselwirkung und wechselwirkt zudem auf Grund des Higgs-Mechanismus mit allen anderen Teilchen, bis auf das Photon und das Gluon. Denn diese beiden Teilchen haben keine Masse. Letztlich lässt sich noch eine sehr abstrakte Eigenschaft des Higgs-Teilchens dieser Liste hinzufügen. Nämlich, dass es ein skalares Teilchen ist. Das bedeutet, dass dieses Teilchen aus dem Vakuum entstehen kann und ebenso wieder im Nichts verschwindet. Dabei ist zu beachten, dass nach dem Energieerhaltungssatz genauso viel Energie aus dem Vakuum herausgesaugt wird, wie dann wieder an die anderen Teilchen in Form von Masse abgegeben wird.
Um aber nun zu verstehen, wo die Masse denn herkommt, muss man auch den Higgs-Mechanismus verstehen. Diesen genau zu erklären, überschreitet aber meine Fähigkeiten in der theoretischen Physik und Mathematik. Zur komplexen Erklärung kann ich nur ein wenig andeuten. Das SM wird mathematisch durch sogenannte Eichsymmetrien erklärt. Das Problem des SM ist aber dann, dass die Masseterme die Eichvarianz der Lagrange-Dichte verletzen. Diese ist bei der Betrachtung von Feldern nötig. Daraus folgt dann, dass die Theorie des SM nicht mehr konsistent ist. Der Higgs-Mechanismus sagt nun aus, dass die vorliegende Verletzung der Symmetrie, nicht durch die Teilchen und deren Masse verursacht wird, sondern das dies dem Grundzustand des Systems, also dem Vakuum, anzulasten ist. Diese Erklärung des Problems wird spontane Symmetriebrechung genannt. Im Folgenden werde ich darauf aber nicht weiter eingehen, da mir die Details deutlich zu komplex sind.
Stattdessen werde ich den Mechanismus anhand einer Analogie aus dem Jahr 1993 von David Miller, der diese zur Frage „Was ist das Higgs-Boson und warum wollen wir es finden?“ verfasste, erklären. In zwei Teilen wird zuerst der Higgs-Mechanismus und dann das Higgs-Boson erläutert.
1.Der Higgs-Mechanismus:
Stellt euch vor, ihr seid auf einer Party einer Partei, bei der alle Anwesenden gleichmäßig im Raum verteilt sind und sich mit ihrem Nachbarn unterhalten. Dann betritt die ehemalige Premierministern den Raum und will ihn durchqueren. Dabei werden alle Party-Gäste stark von ihr „angezogen“ und es bildet sich eine Gruppe von Menschen um sie herum. Sie zieht die Personen an, denen sie sich nähert. Diejenigen, von denen sie sich entfernt, verteilen sich wieder gleichmäßig im Raum. Sie behält zwar ihre Geschwindigkeit bei, trotzdem vergrößert sich ihre kinetische Energie, da sich auf Grund der Gruppe um sie herum auch ihre Masse vergrößert. Daher lässt sie sich, einmal in Bewegung gesetzt, schwerer stoppen, aber auch aus dem Ruhezustand schwerer wieder in Bewegung setzen, weil sich in diesem Fall erst eine neue Gruppe an Menschen bilden muss
Wenn man sich diese Analogie nun in drei Dimensionen vorstellt und die Relativitätstheorie berücksichtigt, ist das der Higgs-Mechanismus. Die Party steht für das Hintergrund-Feld, das sogenannte Higgs-Feld. Diese wird dann, immer wenn sich ein Teilchen hindurch bewegt, lokal gestört. Die Störung in Form der Bildung einer Gruppe an Menschen erzeugt die Masse des Teilchens.
2. Das Higgs-Boson:
Um das Higgs zu verstehen, muss man sich vorstellen, dass sich ein Gerücht im Raum der gleichmäßig verteilten Politiker ausbreitet. An der Tür bilden sich erste größere Gruppen, um mehr über jenes Gerücht zu erfahren. Danach nähern diese Menschen sich dann ihren nächsten Nachbarn, um ihnen ihr Wissen über das Gerücht zu vermitteln. So wandert eine Art Welle von kleinen und großen Gruppen durch den Raum. Diese kann sich bis in alle Ecken ausbreiten, aber auch ein Bündel von Menschen bilden. Weil es sich bei den Informationsüberträgern um eine Menschengruppe handelt und da es jene Gruppenbildung wie bei der Premierministerin war, haben auch die einzelnen Gruppen eine Masse.
Eine solche Gruppe an Menschen steht für das Higgs-Boson.
Ich hoffe, dass es nun etwas verständlicher ist, was genau dieses Teilchen ist und wie der Mechanismus funktioniert. Ich persönlich freue mich schon auf weitere Entdeckungen und Beweise des LHCs. Denn obwohl Elementarteilchen etwas ganz abstraktes sind, sind sie zugleich auch sehr spannend und helfen unserem Verständnis, wie das Universum entstanden ist und woraus wir überhaupt bestehen.











Kommentare (8)