Ich halte Armin Wolf für einen der besten und wichtigsten Journalisten Österreichs (bzw. des deutschsprachigen Raums). Aber bei dem, was er kürzlich auf Facebook über den Mathematik-Unterricht geschrieben hat, bin ich ausnahmsweise einmal anderer Meinung.
Wolf beschreibt in dem mittlerweile weit über tausend Mal geteilten und kommentierten Beitrag seine vielen Besuche in Schulen und die Erfahrung, dass überraschend viele Schülerinnen und Schüler Nachhilfe in Mathematik benötigen:
“Wenn in fast jeder Schule in einem einzigen Fach mehr als die Häfte der Schüler externe Nachhilfe braucht, gibt es ein grundsätzliches Problem (mal abgesehen von der sozialen Ungerechtigkeit, weil Nachhilfe wirklich teuer ist).”
Und damit hat er natürlich absolut recht. Es gibt ein grundsätzliches Problem! Und ich stimme Wolf auch vollkommen zu, was die Bedeutung des Mathematik-Unterrichts angeht:
“Trotzdem halte ich Mathe-Unterricht für extrem sinnvoll und elementar wichtig. Was mich aber immer wieder verblüfft: Dass es unser Schulsystem schafft, zahllose Jugendliche für die Matura zu dressieren, die aber drei Jahre später keine etwas anspruchsvollere Schlussrechnung mehr lösen können oder auf einen Blick erkennen, dass eine Zahlenangabe völlig unrealistisch ist.”
Mathematik ist wichtig und es ist erschreckend, dass das, was man in der Schule lernt, so schnell wieder vergessen ist. Andererseits bin ich mir aber nicht sicher, ob das jetzt etwas ist, was speziell die Mathematik betrifft. Ich vermute mal (und würde mich freuen, falls mich jemand auf eventuell vorhandene Studien hinweist, die das bestätigen oder widerlegen), dass jedes Schulfach, das man nach der Matura (bzw. dem Abitur) nicht mehr aktiv benutzt, schnell vergessen ist.
Wer kann schon, Jahre nach Abschluss der Schule, noch genau die Fachbegriffe aus dem Chemie- oder Biologie-Unterricht reproduzieren? Wer weiß spontan, wie eine Redox-Reaktion abläuft oder kann die Phasen der Mitose reproduzieren? Niemand vermutlich, ausgenommen diejenigen, die sich nach der Schule weiter und vertiefend mit Chemie oder Biologie beschäftigt haben. Redox-Reaktionen oder Mitose treffen wir selten im Alltag und das gilt auch für die mathematischen Begriffe, die Wolf anführt:
“‘Beachte: Das skalare Produkt zweier Vektoren ist kein Vektor, sondern eine reele Zahl.’ Das steht im ‘Kompendium zur Maturavorbereitung’ eines aktuellen Mathe-Schulbuchs. Stimmt ganz sicher, aber wozu muss ein Maturant das nochmal unbedingt wissen? Und da rede ich jetzt noch nicht vom ‘Orthogonalitätskriterium’ (hat damit zu tun).”
Und da sind wir langsam beim Fundament des oben erwähnten grundsätzlichen Problems angekommen. Der Frage nach der Sinnhaftigkeit der Mathematik. Armin Wolf schlägt vor, die verpflichtende Matura-Prüfung in Mathematik (ich bin mir nicht sicher, ob Mathe auch beim deutschen Abitur in allen Bundesländern verpflichtend ist?) abzuschaffen:
“So wie ich auch nicht weiß, warum man in Österreich jedenfalls in Mathe maturieren muss. Würde das nicht als Voraussetzung ausreichen, wenn man Physik oder Technik oder ein anderes Mathe-lastiges Fach studieren will? So wie man von Jus-Studierenden oder Medizinern verlangt, dass sie ein Latinum vorweisen können oder von BWLern, dass sie Grundzüge von Rechnungswesen beherrschen. Und wenn sie aus einer AHS kommen, müssen sie es eben nachlernen. Niemand käme auf die Idee, an allen Schulen eine Rechnungswesen-Matura zu verlangen, nur weil relativ viele 18jährige Wirtschaft studieren.”
Darüber kann man unter Umständen sogar diskutieren. Vielleicht müssen tatsächlich nicht alle Schülerinnen und Schüler am Ende ihrer Ausbildung eine Matura-Prüfung in Mathematik ablegen. Aber selbst wenn man diese Pflichtprüfung abschafft, ändert das meiner Meinung nach nichts an dem fundamentalen Problem. Denn Armin Wolf schlägt ja nicht vor, den Mathematik-Unterricht selbst abzuschaffen. Der wird (und muss) in den Schulen weiterhin stattfinden und die Schülerinnen und Schüler werden sich weiterhin fragen, wozu sie den ganzen Kram brauchen; werden weiterhin von diesem “Angst”-Fach abgeschreckt werden und werden weiterhin Nachhilfe benötigen. Eine abgeschaffte Prüfung am Ende der Schulzeit ändert da nicht viel.
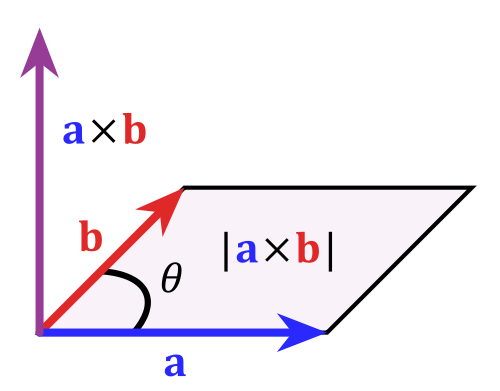
Vektorprodukte schauen nicht nett aus. Tun unregelmäßige Verben aber auch… (Bild: acdx, public domain)
Das Problem liegt – meiner Meinung nach – darin, dass Mathematik nicht so behandelt wird, wie sie behandelt werden sollte und daher auch nicht so gesehen wird, wie man sie sehen sollte. Klar kann man sich fragen, wozu man den Kram mit den Vektoren oder dem “Orthogonalitätskriterium” braucht. Aber dann kann man sich auch fragen, wozu man Wissen über die Monroe-Doktrin, die Reverse Transkriptase oder englische Modalverben braucht.
Aber, werden jetzt sicher einige einwenden wollen, wir müssen doch wissen, was die Monroe-Doktrin ist, wenn wir den Verlauf des zweiten Weltkriegs und damit unsere eigene Geschichte verstehen wollen! Wir müssen über Reverse Transkriptase Bescheid wissen, wenn wir zum Beispiel die Polymerase-Kettenreaktion und damit eine der Grundlagen der Gentechnik, die immer mehr unser Leben bestimmt, verstehen möchten. Und wir müssen die englische Sprache (mitsamt ihrer Modalverben) beherrschen, wenn wir in der globalen Welt von heute auch nur halbwegs bestehen wollen.
Absolut richtig! Aber warum soll all das für die Mathematik nicht gelten? Die Mathematik ist nicht nur schnödes Rechnen und langweiliges Auswendiglernen. Es mag sein, dass sie vielen Schülerinnen und Schülern so präsentiert wird. Dann ist es auch absolut verständlich, wenn dieses Fach gehasst oder nicht verstanden wird. Aber das ist dann den Lehrkräften oder Lehrplänen anzulasten und nicht der Mathematik!
Die Mathematik bestimmt seit Jahrtausenden das Leben der Menschen. Wir haben unsere Zivilisation ebenso der Mathematik zu verdanken wie der Schrift. Mathematisches Wissen ist ebenso ein Kulturgut wie Literatur, Kunst oder Musik. Vor allem aber ist die Mathematik die Sprache mit der man die Welt um uns herum verstehen kann. Das klingt vielleicht ein wenig pathetisch; ist aber deswegen nicht weniger richtig. Wenn wir die Welt in der wir leben verstehen wollen, dann brauchen wir dazu die Mathematik (auf jeden Fall dann, wenn es ein objektives, nachvollziehbares Verständnis sein sein soll). Das gilt für ein Verständnis der unbelebten Natur ebenso wie für ein Verständnis von Gesellschaften, politischen Zusammenhängen, und so weiter: Früher oder später landet man bei einer mathematischen Analyse.
Wenn in der Schule Englisch oder Französisch unterrichtet wird, dann lehrt man dort nicht nur Vokabeln oder Grammatik. Wäre das so, dann wären diese Fächer vermutlich ebenso unbeliebt wie es die Mathematik heute ist. Man muss natürlich Vokabeln und Grammatik lernen, ohne das geht es nicht. Aber man lernt auch, was man mit dieser Sprache anstellen kann. Man erfährt etwas über die französisch- oder englischsprachige Kultur und Geschichte. Über die Länder in denen diese Sprache gesprochen wird. Über die Menschen dort, die Literatur, die Filme, die Küche, und so weiter. Man macht Exkursionen in die entsprechenden Länder und lädt Native-Speaker ein. Kurz gesagt: Man probiert das gesamte Universum dessen zu vermitteln, was diese Sprache ausmacht und wobei sie eine Rolle spielt. Wer in der Schule englisch oder französisch lernt, lernt nicht nur die formalen Eigenschaften einer Fremdsprache kennen, sondern auch die Welt, die von dieser Sprache dominiert wird und in der sie verwendet werden kann.
Genau so sollte es auch mit der Mathematik sein. Mathematik ist eine fremde Sprache und wenn man sie wirklich verstehen will, darf man sich nicht nur auf die Vokabeln und die Grammatik beschränken. Zu wissen, was das “Orthogonalitätskriterium” ist, ist wichtig (ebenso wichtig wie zu wissen, wie man être richtig konjugiert): Zwei Vektoren stehen genau dann orthogonal (also im rechten Winkel) zueinander, wenn ihr Skalarprodukt gleich null ist. Diese Definition muss man – genau so wie das “suis, es, est, sommes, êtes, sont” – irgendwann einmal erklärt bekommen und dann auswendig lernen. Aber man sollte dann auch erklärt bekommen, was man mit diesem Wissen über die Welt erfahren kann!
Die “Grammatik” von Vektoren und Winkeln braucht man zum Beispiel, wenn man über den Raum “reden” möchte. Wenn es in Science-Fiction-Filmen oder Büchern um “fremde Dimensionen” geht, um “parallele Universen”, die neben unserem aber in einer “anderen Richtung” existieren, oder wenn Wissenschaftlerinnen und Wissenschaftler von der vierdimensionalen Raumzeit sprechen; von zusätzlichen Dimensionen in der String-Theorie; Warp-Antrieben, Wurmlöcher, und so weiter: Dann ist es meistens nicht schwer, ein Publikum zu finden, das von solchen Themen enorm fasziniert ist (und oft sind es die gleichen Jugendlichen, die den Mathe-Unterricht nicht leiden können).

Dimensionen sind faszinierend (Bild: Jason Hise, gemeinfrei)
Wenn man aber nicht nur fasziniert sein möchte, sondern das Fundament dieser Faszination auch verstehen will, dann muss man sich unter anderem mit orthogonalen Vektoren beschäftigen. Dann muss man sich klar machen, dass unser dreidimensionaler Raum von drei zueinander jeweils orthogonalen Vektoren aufgespannt wird und wir uns keinen vierten Vektor vorstellen können, der zu den drei vorherigen ebenfalls orthogonal ist. Weswegen es auch unmöglich ist, uns einen vier- oder mehrdimensionalen Raum vorzustellen. Mit der richtigen Sprache und der richtigen Grammatik können wir solche Räume aber beschreiben, analysieren und erforschen. Wer ein bisschen mehr wissen will: Hier, hier und hier habe ich genau diese Themen ausführlich behandelt.
Aber ich vermute, in den wenigstens Schulklassen wird der Unterricht über das Orthogonalitätskriterium von Geschichten über andere Dimensionen und Wurmlöcher begleitet. Man wird im Mathematik-Unterricht auch eher selten Exkursionen veranstalten oder “Native-Speaker” einladen (in meiner Schulzeit zumindest gab es nichts davon). Ich kenne zwar einige Mathematik-Lehrerinnen und -Lehrer die sich sehr bemühen und genau das tun. Die in ihren Klassen nicht nur Mathe-Vokabeln und Mathe-Grammatik unterrichten, sondern das ganze faszinierende Universum vermitteln, das einem die Kenntnis dieser Sprache eröffnet. Aber das sind Einzelfälle. Und genau das ist das Problem.
Armin Wolf schreibt:
“Ich kenne erstaunlich viele Menschen, die der Mathematik-Unterricht so abgeschreckt hat, dass sie heute in der Sekunde nervös werden, wenn man ihnen eine ganz simple Rechenaufgabe stellt. Das kann doch nicht der Sinn der Sache sein.”
Absolut! Das kann, soll und darf nicht der Sinn der Sache sein! Wenn Schulunterricht so endet, dann hat er in jeder Hinsicht versagt. Ebenso wie etwa Deutsch-Unterricht versagt hat, wenn die Aufforderung einen Satz zu lesen, Menschen “in der Sekunde nervös” werden lassen würde.
Meiner Meinung nach (und mir ist klar, dass es sich um ein Thema handelt, das definitiv mehr Analyse benötigt und verdient hat) lautet die Antwort auf die Frage “Was läuft im Mathe-Unterricht falsch”? so: Mathematik ist eine Sprache. Im Gegensatz zum Unterricht in anderen Fremdsprachen werden im Mathe-Unterricht aber nur Vokabeln und Grammatik unterrichtet und der ganze Rest des Sprach-Universums weitestgehend ignoriert. Es ist absolut kein Wunder, dass so ein Unterricht Schülerinnen und Schüler abschreckt!
Man kann von mir aus gerne darüber diskutieren, ob es eine verpflichtende Mathematik-Maturaprüfung geben sollte. Ich persönlich sehe keinen Grund, sie abzuschaffen beziehungsweise genau so viele oder wenige Gründe sie abzuschaffen, wie man etwa eine verpflichtende Deutsch-Matura abschaffen sollte. Ob alle Schülerinnen und Schüler zur Mathe-Matura antreten müssen oder nicht, ändert nichts am grundlegenden Problem. Und das liegt in der falschen Vorstellung dessen, was Mathematik ist.
Ja, Mathematik ist ein Instrument; sie ist ein Werkzeug; sie ist eine Technik die man beherrschen muss, wenn man bestimmte Probleme verstehen oder lösen will. Aber genau so sind Deutsch oder Englisch Instrumente, Werkzeuge und Techniken die man beherrschen muss, wenn man bestimmte Probleme verstehen oder lösen will! Hier ist uns allerdings bewusst, dass diese Sprachen außerdem noch viel mehr sind. Ein Stück von William Shakespeare ist mehr als Instrument, Werkzeug oder Technik! Die Texte von Tocotronic (um jetzt nicht immer nur die Klassiker ins Feld zu führen) sind mehr als Instrument, Werkzeug oder Technik! Sie sind etwas, das mit dem Instrument der Sprache erschaffen wurde und aus dieser Schöpfung sind wieder ganz neue Universen entstanden, die zu erforschen enorm faszinierend ist. Dazu muss man die Sprache aber nicht nur formal beherrschen, sondern auch wissen, was aus ihr alles erwachsen kann.
All das wird beim Unterricht der mathematischen Sprache viel zu oft ignoriert. Und genau das ist es, was im Mathe-Unterricht falsch läuft!











Kommentare (118)