 Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2018. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2018. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————
Mathematische Detektivarbeit – Vom Lösen eines Integrals
von Lucas Treffenstädt
Ich bin Promotionsstudent an einem Lehrstuhl für theoretische Physik an der Universität Bayreuth. Über meine Promotion berichte ich regelmäßig in meinem Podcast “Making a Physicist”. Die Zeichnungen sind, sofern nicht anders angegeben, von meiner Frau Lisa.
Kopfschüttelnd steht Privatdetektiv Newtnitz vor dem Tatort. Eine dunkelgrüne Tafel, dicht beschrieben in zwei Zeilen. Die erste Zeile, ein schier undurchdringlicher Wust von Symbolen, spärlich durchsetzt von einzelnen Zahlen, und dort, ganz links: gleich vier der gefürchteten Integralzeichen! Die zweite Zeile dagegen ist ein Ausdruck voll Eleganz und Präzision. Dazwischen: Ein Gleichheitszeichen! Doch irgendetwas stimmt hier nicht – diese Terme sollen gleich sein? Der Detektiv legt seinen Hut beiseite und runzelt die Stirn. Irgendwie muss dieser Schurke das Integral gelöst haben. Und die Spur ist noch ganz frisch…

Detektiv Newtnitz untersucht seinen neusten Fall. (Bild selbst erstellt aus Vorlagen in Public Domain und Creative Commons (CC0))
Das Telefon schrillt. Newtnitz schreckt aus seinem Nachmittagsnickerchen hoch. Ein neuer Fall? Schnell nimmt er den Hörer ab.
“Der Doktorand hat wieder zugeschlagen! Kommen Sie schnell!”
Sofort ist die Müdigkeit verflogen. “So so, der Doktorand, der alte Schurke. Bin schon auf dem Weg.”.
Newtnitz schlüpft schnell in seinen langen Mantel, zieht sich den Schlapphut tief in die Stirn und eilt zum Tatort.
Es ist eine dunkelgrüne Tafel, gewöhnliches Fabrikat, an einer Wand in einem verlassenen Hörsaal. Mit weißer Kreide hat jemand eine Gleichung darauf gekritzelt:
Die Handschrift ist eindeutig. Der Doktorand. Keiner weiß, was sich in seinem wirren Kopf abspielt. Aber um diesen Fall zu lösen, muss Detektiv Newtnitz die Rechnung nachvollziehen und Schritt für Schritt zur Lösung finden.
Zunächst mal das Offensichtliche: Integriert (keine Ahnung, was Integrale sind? Hier gibt es zwei Videos) wird über Theta, Phi, Theta-Strich und Phi-Strich. “Dann werden die restlichen Symbole wohl Konstanten sein.” murmelt Newtnitz und beginnt, in sein Notizbuch zu kritzeln. “Dann können wir diesen Teil ja mal vor das Integral schreiben.”
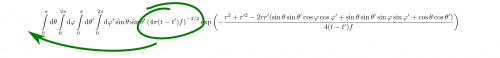
Konstante Faktoren können vor das Integral gezogen werden. Ob ich eine Funktion mit einer Konstanten multipliziere und dann integriere oder erst integriere und dann multipliziere, ist also egal. selbstgemacht)
War’s das schon an Konstanten? “Nein, da musst du dich schon besser verstecken, wenn du meinem scharfen Auge entgehen willst!”.
Die Exponentialfunktion lässt sich zerlegen. Aus einer Summe im Exponenten kann man ein Produkt mehrerer Exponentialfunktionen machen.
Aber Vorsicht, nicht den Bruchstrich vergessen! “Aha, da haben wir ja eine weitere Konstante.”
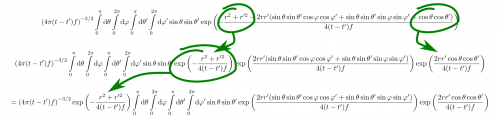
Durch eine Eigenschaft der Exponentialfunktion lässt sich ein weiterer Faktor aus dem Integral ziehen. Beim Aufteilen der Summe müssen natürlich beide Teile den Bruchstrich mitnehmen. (selbstgemacht)
“Das sieht aber immer noch nicht gut aus.” Der Detektiv wischt sich über die Stirn. “Aber Moment mal… der Sinus, der ist doch doppelt. Hehe, dich krieg ich!”
Und damit wird ein Term ausgeklammert, wieder wird ein Teil etwas übersichtlicher. Übrig bleibt eine Summe von einem Sinus- und einem Kosinus-Term.
“coco plus sisi? Hmm… alte Detektivregel: cos(x-y) = cos(x)cos(y)+sin(x)sin(y).” Newtnitz nickt zufrieden.
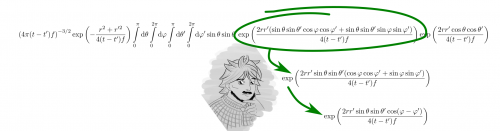
Gemeinsame Faktoren in einer Summe kann man ausklammern. Die restliche Summe kann mit einem sogenannten Additionstheorem vereinfacht werden. Additionstheoreme sind Regeln für Summen von trigonometrischen Funktionen wie Cosinus und Sinus. (selbstgemacht)
Aber noch ist keines der Integrale ausgewertet. Newtnitz kneift die Augen zusammen. Muss er das überhaupt in der Reihenfolge auswerten, wie es da steht?
“Dieser Schurke meint wohl, er kann mich verscheißern. Die Grenzen sind ja alle unabhängig! Mal sehen…” Er schreibt die Integralzeichen in einer anderen Reihenfolge.
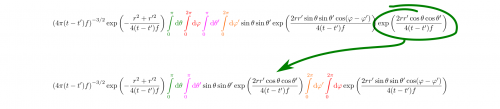
Bei der Auswertung mehrerer verschachtelter Integrale kann die Reihenfolge beliebig vertauscht werden, wenn die Grenzen nicht voneinander abhängig sind. Das bedeutet auch, dass ich Teile, die nur von manchen der Integrationsvariablen abhängen, an den Integralen vorbeiziehen kann, von denen sie nicht abhängen. (selbstgemacht)
Kann er nun eines der Integrale auswerten? Die beiden Phis sehen doch irgendwie verdächtig aus. Sie kommen schließlich nur in einem Cosinus vor, und das ist eine periodische Funktion. Und die Integrale gehen auch noch über die ganze Periode, also einmal im Kreis. “Na klar! Das Phi-Strich ist völlig irrelevant! Egal, wo ich im Kreis anfange, solang ich ihn einmal ablaufe, bekomme ich dasselbe Ergebnis!”
Zack! Das Phi-Strich wird gestrichen. “Und was bleibt von dem Phi-Strich-Integral übrig? Der Integrand ist konstant – also nur die Differenz der Grenzen: 2 Pi!”.
Ein Integral erledigt – drei verbleiben. Newtnitz gönnt sich ein Grinsen. “Dich hab ich gleich, Halunke!”.
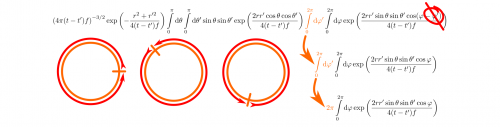
Eine periodische Funktion wiederholt sich immer wieder. Es ist daher egal, wo man mit der Integration beginnt, solange man dort auch wieder endet, also eine komplette Periode durchläuft. Ein Integral mit konstantem Integranden ergibt immer nur die Größe des Integrationsgebietes. (selbstgemacht)
Dann also das andere Phi-Integral. “Das kann doch eigentlich nicht so schwierig sein – eine Exponentialfunktion mit einem Cosinus… hmm.”. Eifrig kritzelt er los. Doch die Euphorie über das gelöste Integral verfliegt bald. Partielle Integration, Substitution – keiner der üblichen Detektivtricks hilft.
“Zeit für einen Kaffee” brummt Newtnitz und zückt sein Handy. “Hey Bronstein, alte Socke! Lust auf einen Kaffee? Ich brauch mal deine Hilfe bei einem Fall.”
Kurze Zeit später trifft der Detektiv im Café Lebesgue (“Café Lebesgue: Kaffee und Gebäck”) ein. Ein schmieriger Laden, aber der Kaffee ist gut. An einem Ecktisch sieht er schon Bronstein sitzen.
Nach einer knappen Begrüßung sitzen die beiden sich gegenüber, zwei dampfende Tassen zwischen sich. Von draußen schlägt dichter Herbstregen gegen die Fenster.
“Dann mal raus mit der Sprache, wo drückt der Schuh?” fragt Bronstein. Schweigend kritzelt Newtnitz ein paar Symbole auf eine Serviette.
“Was isn das Alpha?” – “Ach, bloß irgendeine Konstante.”
Bronstein grübelt einen Moment.
“Tut mir leid, keine Ahnung.” – “Verdammt. Das ist wirklich wichtig.” – “Pass auf, ich kenn da einen Typ. Wolfram. Hab ihn noch nie persönlich getroffen, aber ich weiß, wo er sich im Internet rumtreibt.” – “Du möchtest, dass ich irgendeinem Typen aus dem Netz vertraue?” – “Er ist schon okay. Manchmal ein bisschen schwer von Verstand, aber wenn er was rafft, dann gibt er schon ne ordentliche Antwort. Hier, kannst mein Smartphone verwenden, deine alte Gurke schafft das ja nicht.”
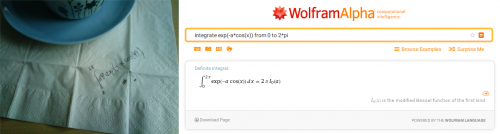
Wenn man nicht weiter weiß, hilft manchmal ein Blick ins Buch oder ins Internet. Aber auch wolfram|alpha kann nicht jedes Problem lösen (probiert es doch mal mit anderen Teilen dieses Integrals). (selbstgemacht, Screenshot von wolframalpha.com)
“Tatsächlich. Ja, da muss ich nur noch für A die Vorfaktoren von meinem Cosinus einsetzen.” – “Sag ich doch. Und das ist jetzt die Lösung zu deinem Fall?” – “Naja, nicht ganz. Das ist nur ein Teil eines größeren Integrals. Zwei von vier hab ich jetzt gelöst. Hier, so schaut es jetzt insgesamt aus.” – “Puh, das ist aber ziemlich hässlich. Sinus, Cosinus, Exponentialfunktion und dann auch noch eine Besselfunktion? Da kann dir der Wolfram auch nicht mehr weiterhelfen. Ich fürchte, da wirst du dich in zwielichtigere Gegenden begeben müssen.” – “Denkst du da an jemand speziellen?” – “Naja. Bin mir nicht sicher, ob du das wirklich willst. Der Typ heißt Gradshteyn, ist öfter unten am Hafen zu treffen. Hängt da mit seinem Kumpel Ryzhik rum. Aber pass bloß auf, die Typen sind knallhart.” – “Ich kann auf mich aufpassen. Danke für den Tipp.”
Newtnitz wirft einen Fünfer auf den Tisch und verschwindet durch die leicht klemmende Eingangstür. Bronstein lehnt sich zurück und nimmt einen großen Schluck aus seiner Tasse. “Soll bloß nicht sagen, ich hätte ihn nicht gewarnt.”
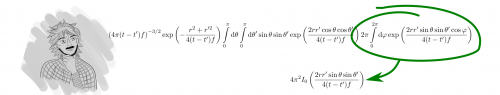
Zum Nachschlagen eines Integrals ist es sinnvoll, mehrere Konstanten zu einer zusammenzufassen und danach wieder einzusetzen. Was muss man hier für A aus der Lösung von wolfram|alpha einsetzen? (selbstgemacht)
Der Hafen. Es dämmert schon. Der kalte Herbstregen peitscht hier noch heftiger auf den Detektiv ein. Trotz dem großen Schlapphut läuft ihm Regenwasser in den Kragen.
“Ich hasse diese Gegend.”
Aus einer Kneipe an der Ecke dringt durch schmutzige Scheiben trübes Licht auf die Straße. Hier muss es sein.
Von innen sieht die Kneipe noch schäbiger aus als von außen, was wirklich etwas heißen soll. Das Klientel ist nicht weniger schäbig.
Am Tresen putzt eine Dame gehobenen Alters gelangweilt mit einem Lappen über die Arbeitsfläche. “Was darf’s denn sein, Schätzchen?”
Newtnitz schielt zu den Biergläsern. “Ich bin nicht hier um zu trinken. Ich brauche Information.” – “So, so. Und was für eine Art Information sollte ein unschuldiges Täubchen wie ich schon haben?” – “Du vielleicht nicht. Aber ich hab von jemandem gehört, der etwas wissen könnte. Sagt dir der Name Gradshteyn was?”
Die Bardame wirft einen flüchtigen Blick auf eine unauffällige Tür neben dem Tresen. “Nie gehört.”
Gerade möchte Newtnitz etwas erwidern, da wird besagte Tür mit einem Krachen aufgeschlagen. Zwei zwielichtige Gestalten treten hindurch. Es ist plötzlich totenstill im Raum.
“Was bist du denn für ein Vogel?” knurrt der ältere der beiden in Richtung Tresen.
“Ich?” sagt Newtnitz “Ich bin ein Wanderfalke, und ich bin auf Rattenjagd.”
“Pass bloß auf, diese Ratten könnten bissig sein!” erwidert der andere gereizt.
“Na wenn ihr so hart seid, dann könnt ihr doch bestimmt das hier lösen.” sagt Newtnitz und wirft den Gestalten einen zerknüllten Zettel zu.
Der ältere fängt den Zettel auf, entfaltet ihn und wirft einen kurzen Blick darauf.
“Pah. Warum sollten wir uns mit so was abgeben? Und dann auch noch von jemandem, der nicht mal die simpelsten Vereinfachungen machen kann?”
Newtnitz runzelt für einen Moment die Stirn. Dann hat er eine Idee. Er schnappt sich den Zettel und kritzelt eine neue Zeile.
Mit einem Grinsen gibt er ihn dann zurück an das Duo.
“Variablensubstitution. Wir benutzen einfach den Cosinus selbst als Integrationsvariable. Den Sinus kann man damit auch darstellen. Und die beiden Sinusterme vor der Exponentialfunktion werden wir sogar durch die Funktionaldeterminante los.”

Variablensubstitution ist ein wichtiger Trick, um Integrale zu vereinfachen. Eine Teil einer Funktion wird durch eine neue Variable ersetzt, mit der sich insgesamt hoffentlich ein einfacherer Integrand ergibt. Dieses Video erklärt euch das etwas ausführlicher. (selbstgemacht)
Die beiden finsteren Gestalten werfen erneut einen Blick auf den Zettel. “Du hast ganz schön Eier, hier aufzutauchen und mit solchen Formeln um dich zu werfen.” sagt der ältere. “Aber du hast Glück. Wir mögen Kerle mit Eiern. Hier, nimm das und verzieh dich.”
Mit diesen Worten schmiert der andere zwei Zeilen auf das Papier, knüllt es zusammen und wirft es Newtnitz zu. Dieser möchte sein Glück nicht länger strapazieren und verlässt die Kneipe.
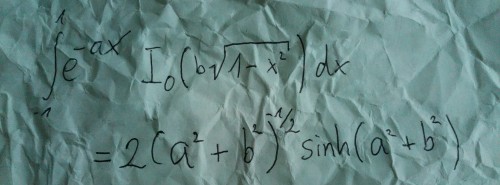
Das Buch “Table of Integrals, Series and Products” von I. S. Gradshteyn und I. M. Ryzhik ist ein absolutes Monster. Auf über 1200 Seiten sind alle erdenklichen Integrale aufgeschrieben, für die Lösungen bekannt sind. (selbstgemacht)
Zurück in seinem Büro, glättet Newtnitz den Zettel, den er in der Kneipe erhalten hat. Tatsächlich: Die Formel lässt sich auf das Integral über Theta-Strich anwenden.
Und das Ergebnis ist sogar unabhängig von Theta! Das letzte Integral ist damit auch nur noch ein konstanter Faktor.
Erschöpft lehnt sich der Detektiv in seinem Stuhl zurück und vergleicht sein Ergebnis mit der Formel des verbrecherischen Doktoranden.
Es sieht ähnlich aus. Sehr ähnlich.
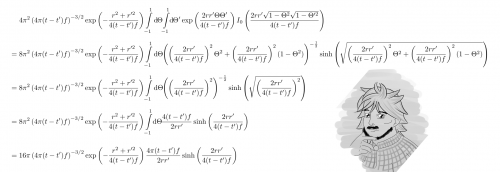
Versuche selbst, die Variablen a und b aus Gradshteyns Formel zu identifizieren. Es ist verblüffend, wie sich die Terme gegenseitig eliminieren, so dass keine Abhängigkeit von Theta mehr übrig bleibt. (selbstgemacht)
Doch diese Funktion, die noch verbleibt – ein Sinus Hyberbolicus! Den kann man doch umformen – richtig, in eine Summe zweier Exponentialfunktionen!
Das ist es! So hat der Doktorand es geschafft. Und jetzt weiß Newtnitz auch, wo er ihn finden kann. Wie sonst hätte Gradshteyn so schnell die richtige Formel zur Hand haben sollen?

Natürlich kann man die Regel mit den Produkten von Exponentialfunktionen auch rückwärts anwenden. Der letzte Schritt ist dann einfach – erinnerst du dich noch an die binomischen Formeln? (selbstgemacht)
Knall! Triefend nass und von seinem Rücken mit Blitzen erleuchtet, steht Detektiv Newtnitz im Eingang der Hafenkneipe. Der Raum ist leer, bis auf einen runden Tisch in der Mitte, an der drei Karten spielende Gestalten sitzen: Gradshteyn, Ryzhik und… natürlich! Wie konnte er nur so blind sein? Der geheimnisvolle Doktorand, dem er auf der Spur gewesen ist, es ist kein anderer, es konnte kein anderer sein als: Leibton, sein ehemaliger Praktikant.
“Du hast es also gelöst.”
Sagt dieser und erhebt sich langsam von seinem Stuhl.
“Aber hast du dir auch nur einen Moment lang Gedanken darum gemacht, warum ich es getan habe?”
Newtnitz, der eben noch auf ihn zurennen wollte, um ihn zu überwältigen, stockt.
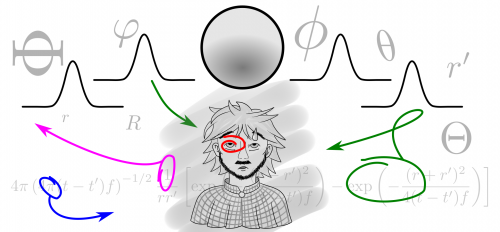
“Natürlich nicht. Du purer Mathematiker hast nicht mal daran gedacht, dass jemand damit einen Zweck verfolgen könnte, Integrale zu lösen. Für dich sind Theta, Phi und r nur Symbole. Für mich jedoch sind sie KUGELKOORDINATEN!” Es donnerte. “Und was du berechnet hast, ist nichts geringeres als eine gaußsche Wechselwirkung in einem isotropen System!”
Wie vom Donner gerührt steht der Detektiv in der Kneipe. Es ist zu viel Vor seinem geistigen Auge kreisen Sphären, tauschen Kugelschalen Kräfte aus, dabei rotiert die ganze Welt und NICHTS VERÄNDERT SICH…
Vom Zuschlagen einer Tür wird Newtnitz aus seiner Verwirrung gerissen. “Verdammt!” Leibton ist entwischt. Fürs erste. Eines Tages wird er ihn erwischen. Er wird ihn erwischen und dieser ekligen angewandten Mathematik ein Ende bereiten…

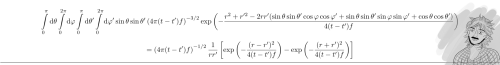











Kommentare (37)