Nach der Allgemeinen Relativitätstheorie ist ja die Raumzeit gekrümmt, das hat vermutlich jeder schon mal gehört. Veranschaulicht wird das oft mit gekrümmten Flächen im Raum. Aber wie krümmt man die Raum-Zeit? Und wenn man sich das mit gekrümmten Flächen vorstellen soll, worin ist denn die Raumzeit gekrümmt? Gibt es einen Hyperraum?
Bilder wie dieses Bild eines Wurmlochs
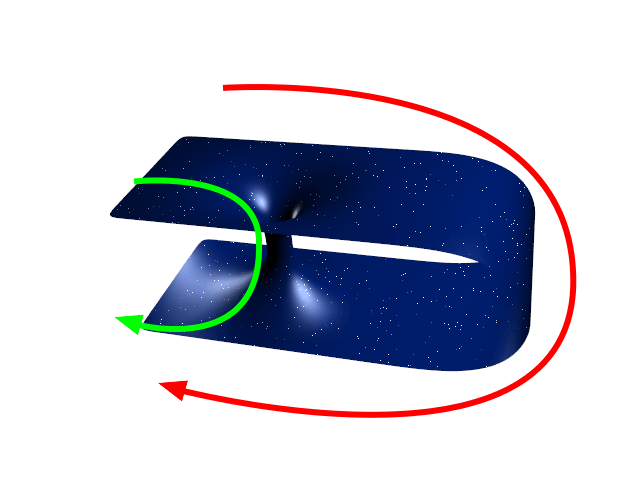
Von Panzi – English Wikipedia, CC BY-SA 3.0, Link
scheinen ja zu suggerieren, dass die Raumzeit irgendwie in einen höheren Raum “eingebettet” ist.
Hier will ich versuchen, euch (und mir selbst, beim Schreiben lernt man ja am meisten) anschaulich zu erklären, wie das mit der Raumzeitkrümmung funktioniert und warum man keinen Hyperraum braucht. Stattdessen verwenden wir Landkarten mit seltsamen Maßstäben.
Eine “Plattkarte” der Erde
Für den Anfang braucht ihr erstmal einen Globus, oder zumindest ein Bild von einem:
By Stefan Kühn – Own work, CC0, Link
Kartographinnen stehen ja schon seit Jahrhunderten vor dem Problem, wie man möglichst genaue Karten der kugelförmigen Erde anfertigt. Man kann die Oberfläche der Erde ja nicht einfach auf ein flaches Stück Papier abbilden, ohne dass sich irgendwas verzerrt, eben weil die Erdoberfläche gekrümmt ist. (Wer’s nicht glaubt, kann folgendes einfache Experiment machen: Eine Mandarine so schälen, dass die Schale in einem Stück bleibt, und dann versuchen, die Schale flach auf den Tisch zu legen.)
Eine einfache Möglichkeit der Abbildung (allerdings keine besonders übliche) besteht darin, das oben eingezeichnete Netz aus Längen- und Breitengraden auf ein Karopapier zu übertragen (der Fachterminus dafür ist, wie ich gerade auf Wikipedia gelernt habe, “Plattkarte”). So sieht unsere Erde aus:

Von original by NASA (sensor Terra/MODIS), modified by Mdf – https://visibleearth.nasa.gov/: Info, Image. Modified by Mdf, Gemeinfrei, Link
Wie man erkennen kann, ist die Karte insbesondere in der Nähe der Pole nicht so toll – genau an den Polen gehören ja zu einem einzigen Wert des Breitengrades alle möglichen Längengradwerte. (Die häufig verwendete Mercator-Projektion sieht etwas anders aus, sie vergrößert die Bereiche, die weiter vom Äquator entfernt sind. In den Siebziger Jahren wurde sie deshalb als “eurozentristisch” eingestuft und alternative Kartenentwürfe wurden vorgeschlagen. Bei Wikipedia findet ihr mehr dazu.)
Im folgenden betrachte ich deshalb nur einen Ausschnitt aus dieser Karte, der den Nordpol nicht mit einschließt:
Eingezeichnet habe ich jetzt auch Werte für die Grade an den Längen- und Breitengraden; damit es überschaubar bleibt, konzentriere ich mich auf die nördliche Breite und östliche Länge.
Die Linien haben einen Abstand von jeweils 15Grad. Der räumliche Abstand ist aber komplizierter: Der Abstand zwischen zwei Breitengraden ist immer gleich – 15Grad machen so etwa 1667km Kilometer aus (da die Erde nicht perfekt kugelförmig ist, gibt es da ne leichte Korrektur, wer will, kann die bei Wikipedia nachlesen). Längengrade rücken aber ja immer dichter zusammen, je näher ich dem Pol komme. Entsprechend ändert sich auch der Abstand zweier Längengrade mit zunehmendem Breitengrad: Am Äquator ebenfalls 1667km für 15°, aber je weiter man nach Norden geht, desto kleiner wird der Wert. Oben am Bild der Längengrade auf der Kugel (oder noch besser an eurem Globus) könnt ihr das leicht sehen.
Wie die Karte die Raumkrümmung zeigt
Und in dieser Längenänderung steckt jetzt schon das Geheimnis der Raumkrümmung (die Raumzeit krümmen wir anschließend). Stellt euch zunächst vor, ihr startet bei 45° nördlicher Breite und 0°Länge (so etwa irgendwo in den Pyrenäen). Von dort aus geht ihr 3546km nach Osten, das sind gerade 45°Länge, landet also kurz vor dem Aralsee Kaspischen Meer (ähem, Geografie war noch nie meine starke Seite, danke, Saintman). Anschließend fliegt ihr 5001km nach Süden, so dass ihr knapp südlich vom Horn von Afrika im Meer landet. In folgendem Bild ist das die grüne Route:






Kommentare (141)