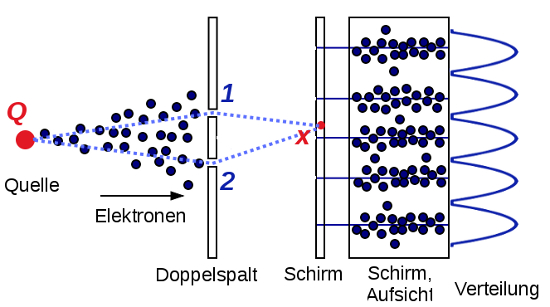
Quantenmechanische Objekte benehmen sich ja bekanntlich seltsam: Schickt man ein Elektron, das ja ein einzelnen Teilchen ist, durch einen Doppelspalt, dann sieht man hinter dem Spalt ein Seltsames Muster aus hellen und dunklen Streifen. Dieses Muster kommt dadurch zu Stande, dass das Elektron zwei Möglichkeiten hat, durch den Doppelspalt zu gehen: oben und unten:
So etwa sieht das aus:
(Bild gemeinfrei, modifiziert von Wikipedia.)
Man kann das Phänomen – je nachdem, welche Beschreibungsart der Quantenmechanik man wählt – unterschiedlich erklären, aber in irgendeiner Weise geht das Elektron durch beide Spalte zugleich und kann deshalb mit sich selbst wechselwirken. (Ausführlich habe ich das Experiment hier erklärt.)
Wiederholt man das gleiche Experiment mit “gewöhnlichen” Teilchen (also beispielsweise kleinen Kugeln), dann ergibt sich natürlich ein anderes Bild: Es gibt zwei Maxima der Verteilung, eins hinter jedem Spalt. In unserem Alltag gilt nun mal die klassische Physik, und solche seltsamen Phänomene beobachten wir nicht.
Aber wo ist der Übergang zwischen der Quantenmechanik und der klassischen Physik? Wie groß kann man ein System machen und immer noch Quanteneffekte beobachten? Diese Frage hat ja schon Schrödinger mit seinem berühmten Katzenexperiment (dieses Bild kann ich aus Copyright-Gründen nicht einfügen) gestellt: Könnte selbst ein makroskopisches Objekt wie eine Katze in einem quantenmechanischen Überlagerungszustand sein und damit gleichzeitig tot und lebendig? Da wir das noch nie beobachtet haben, scheint irgend etwas das zu verhindern. Ist das nur unsere Wahrnehmung (wie zum Beispiel in der Viele-Welten-Theorie, wo alle Überlagerungen existieren, wir sie aber nie gleichzeitig wahrnehmen können), oder passiert tatsächlich etwas physikalisch Neues, wenn Quantensysteme sehr groß werden?
Um das zu untersuchen, versucht man, Quanteneffekte an immer größeren Systemen zu beobachten.
Einem Forscherteam aus Österreich ist es jetzt gelungen, ein ähnliches Experiment wie den Doppelspalt (nämlich einen Mehrfachspalt) mit großen Molekülen aufzubauen, die aus vielen Atomen bestehen und etwa zwei Millionen mal schwerer sind als Elektronen.
Dazu haben sie Farbstoffmoleküle durch ein Gitter aus einer nur wenige Nanometer dicken Keramik geschickt, das mit Spalten im Abstand von etwa 100 Nanometer versehen war, und sie dann mit einer Kamera direkt beobachtet.
So sieht das ganze aus (aus irgendeinem Grund hat Youtube zwei Versionen des Videos, eine davon (mit der Hintergrundmusik von “Der Dritte Mann”) lässt sich nicht einbetten, deshalb nehme ich die andere, aber um eure Nerven zu schonen empfehle ich, den Ton abzuschalten (auch wenn die Musik angeblich explizit komponiert wurde, um den Welle-Teilchen-Dualismus im Ton einzufangen, für mich fällt es unter die Rubrik “Plastikgedudel” (bei 0:36))):
Ihr könnt hier direkt sehen, wie die einzelnen Moleküle an unterschiedlichen Positionen auftauchen und wie sich trotzdem am Ende ein schönes Interferenzmuster bildet.
Es ist nicht das erste mal, dass man Quanteneffekte an ganzen Molekülen gezeigt hat (es ist beispielsweise auch schon mit Fullerenen gelungen), aber ein so schönes Video dazu hat es meines Wissens bisher nicht gegeben.
Zumindest molekülgroße “Schrödinger-Katzen” sind also möglich.
Mehr zu den Experimenten der österreichischen Gruppe findet ihr auf deren homepage.
Das aktuelle Heft von “Spektrum der Wissenschaft” enthält übrigens einen sehr ausführlichen (und guten) Artikel zum Thema “Wie groß können Quantensysteme werden”.






Kommentare (25)