Nein, in diesem Artikel geht es nicht darum, Sudoku-Hefte zu verbrennen. Aber mit etwas Phantasie kann man Sudokus tatsächlich als physikalische Objekte behandeln und dabei etwas über Thermodynamik lernen.
Sudokus sind ja bekanntlich Zahlenrätsel. Auch wenn ihr nie vom Sudoku-Fieber infiziert wart (war ich auch nie, habe nur einige Samurai-Sudoku und eine Handvoll leichter Killer-Sudoku gelöst) kennt ihr vermutlich die Regeln: Man hat ein Raster mit 9×9 Feldern und muss die Ziffern von 1 bis 9 so verteilen, dass in keiner Zeile, Spalte und in keinem Block eine Ziffer doppelt vorkommt. Am Anfang hat man bestimmte Hinweise, nämlich Felder, in denen schon Zahlen drinstehen. So sieht so etwas aus (geklaut von Wikipedia):

Von Wikipit – Eigenes Werk, CC BY-SA 3.0, Link
Und hier ist die Lösung:
Von Wikipit – Eigenes Werk, CC BY-SA 3.0, Link
Mit Physik hat das erst mal nicht viel zu tun, oder?
Aber PhysikerInnen haben ja manchmal eine seltsame Art zu denken und sehen die Welt auf ihre ganz eigene Weise. Und wenn man ein Sudoku mit PhysikerInnen-Augen ansieht, dann fällt einem vielleicht die Ähnlichkeit zu einigen physikalischen Modellen auf. Genau das haben A. Williams und G. Ackland getan – wobei ich auf den Artikel nur aufmerksam wurde, weil ich mit Graeme Ackland an einem gemeinsamen Projekt beteiligt war und ihn deshalb ein bisschen kenne.
In der Thermodynamik geht es ja darum, wie physikalische Systeme sich bei unterschiedlichen Temperaturen verhalten. Darüber kann man dicke Bücher schreiben (ich empfehle z.B. das von Reif), aber da das hier ein Blog-Eintrag ist, mache ich’s kurz (wobei das natürlich relativ ist, die kürzesten Blogeinträge der Welt schreibe ich ja nicht gerade). Eine etwas längere Einführung in viele thermodynamische Konzepte findet ihr natürlich auch hier auf dem Blog.
Das Grundprinzip hinter der Thermodynamik ist ziemlich simpel: Wir brauchen ein System, das in verschiedenen Zuständen existieren kann. Beispielsweise unser Sudoku: Wir können uns vorstellen, dass jedes der 81 Felder einen der 9 möglichen Werte annehmen kann (die meisten Kombinationen geben aber natürlich kein korrekt gelöstes Sudoku, sondern Unsinn). Damit haben wir dann 81 hoch 9 9 hoch 81 (danke, wereatheist) mögliche Zustände, also immerhin etwa 150 Billiarden (1,5e17) 2 mal 10 hoch 77.
In der Thermodynamik geht es außerdem immer um Temperaturen. Aus dem Alltag wisst ihr schon (auch wenn ihr vielleicht noch nie bewusst darüber nachgedacht habt), dass bei niedrigen Temperaturen Systeme bevorzugt in Zuständen mit niedriger Energie vorliegen. Deshalb gefriert Wasser zu Eis (weil die Eiskristalle energetisch günstig angeordnet sind) oder verdampft bei hoher Temperatur (wobei dann die Bindungskräfte zwischen den Molekülen sehr klein sind, so dass der Energiegehalt steigt). Zur Rolle der Energie habe ich übrigens auch mal was geschrieben.
Temperatur und Energie hängen also irgendwie zusammen. Bevor wir das klären, schauen wir erst einmal, wie man die Energie eines Sudokus definieren kann. Dazu schaut man sich an, wie falsch das Sudoku gelöst ist. Nehmen wir an, das Sudoku ist irgendwie mit Ziffern gefüllt. Klappert jetzt der Reihe nach jedes der 81 Felder ab. Fangen wir links oben an. Jetzt guckt ihr der Reihe nach alle Felder in derselben Zeile (also der obersten) an und jedesmal, wenn dort dieselbe Zahl steht wie im Feld links oben, dann macht ihr einen Strich (Fehler!). Dasselbe tut ihr für alle Felder in derselben Spalte und dann für alle Felder im selben Block. Mit anderen Worten, ihr sucht nach Fehlern – danach, ob diese Zahl, die ihr gerade anguckt, dafür sorgt, dass das Sudoku falsch ausgefüllt wurde. Alle diese Fehlerstriche (für alle 81 Felder) addiert ihr auf. Das ergibt dann eine Gesamtfehlerzahl, die man die Falschheit des Sudoku nennen könnte – aber weil wir Thermodynamik betreiben wollen, nennen wir sie die “Energie”. (Wer spitzfindig ist könnte einwenden, dass wir ja jeden Fehler doppelt zählen – einmal Feld X mit Feld Y, dann nochmal Feld Y mit Feld X. Man könnte alles nochmal durch zwei teilen, um das auszugleichen, aber da es ein konstanter Vorfaktor ist, spielt das hier keine Rolle und wir können das ignorieren.)
Die Energie sagt uns also, “wie falsch” ein Sudoku ausgefüllt wurde. (Ihr könnt also ab jetzt einfach irgendwelche Zahlen in das Sudoku reinschreiben und sagen, dass ihr Hochenergie-Sudokus löst (oder auch “heiße Sudokus” – weil bei hohen Temperaturen ja höhere Energien auftreten).) Den Zustand mit der niedrigsten Energie hat das Sudoku, wenn es korrekt ausgefüllt wurde, dann gibt es keine Fehler, also ist die Energie Null.
Eine Besonderheit des Sudokus als physikalisches System ist, dass der räumliche Abstand zwischen zwei Punkten keine Rolle spielt. Zwei Punkte können sich entweder direkt beeinflussen (wenn sie zur selben Reihe, Spalte oder zum selben Block gehören), oder sie sind über zwei Punkte indirekt verbunden (denn es liegt immer ein Feld in der Reihe des einen und Spalte des anderen Punktes und umgekehrt). Es gibt also nicht die Möglichkeit, dass zwei Punkte “weit entfernt” voneinander liegen wie in anderen physikalischen Systemen.
So, wir haben also ein Sudoku, in dem anfänglich schon Hinweise drinstehen und das wir dann ausfüllen. Dann können wir seine “Energie” berechnen. Jetzt muss noch irgendwie die Thermodynamik ins Spiel kommen.
Dazu brauchen wir jetzt das wichtigste Gesetz der Thermodynamik, das Boltzmann-Gesetz. Es besagt (für Sudokus) Folgendes: Wenn wir unser Sudoku bei einer bestimmten Temperatur angucken (das ist natürlich eine rein fiktive Temperatur, die nichts damit zu tun hat, wo ihr das Sudoku-Heft aufbewahrt), dann können wir jeden denkbaren Zustand unseres Sudokus finden. Allerdings sind nicht alle Zustände gleichwahrscheinlich: Je höher die Energie eines Zustandes ist, desto unwahrscheinlicher werden wir ihn finden. (Mathematisch steckt da eine Exponentialfunktion drin, das findet ihr in der Entropie-Serie erklärt – rechts bei “Artikelserien” klicken.) Die Temperatur regelt dabei, wie viel unwahrscheinlicher ein Zustand mit hoher Energie ist als ein Zustand mit niedriger Energie – ist die Temperatur sehr niedrig, sind Zustände mit hoher Energie extrem unwahrscheinlich, geht die Temperatur gegen unendlich, dann sind auch Zustände mit hoher Energie genau so wahrscheinlich wie Zustände mit niedriger Energie.
“Echte” physikalische Systeme haben eine Dynamik, sie wechseln also von einem Zustand in einen anderen. Dabei können sie ihre Energie ändern, weil sie ja bei einer bestimmten Temperatur betrachtet werden – sie stehen also in Kontakt mit irgendeinem großen Wärmebad, dass sie auf Temperatur hält (beispielsweise ein Ofen, ein Kühlschrank oder so etwas). Wenn man die Energie über lange Zeit mittelt, dann stellt man fest, dass die Wahrscheinlichkeit der Zustände genau der Boltzmann-Verteilung entspricht.
Nun gibt es Sudokus nicht als echte physikalische Systeme und ihr könnt euer ausgefülltes Heft zwar mal für ein paar Stunden in den Ofen schieben, ich bezweifle aber, dass sich dadurch die Zahlen in den Feldern ändern werden (es sei denn, die Temperatur ist zu hoch, dann werden sie vermutlich braun). Wenn ihr aber euer Sudoku in eurem Computer abgespeichert habt, dann könnt ihr dort die Zahlen natürlich auch ändern – und zwar am besten genau so, dass ihr die richtige Wahrscheinlichkeitsverteilung für die Sudokus mit unterschiedlicher Energie bekommt, so dass also Zustände mit hoher Energie unwahrscheinlich und Zustände mit niedriger Energie wahrscheinlicher sind. Passende Algorithmen hat man Mitte des letzten Jahrhunderts ausgeknobelt (ursprünglich, um das Verhalten von Atombomben zu simulieren, inzwischen haben diese Algorithmen aber auch endlos viele nützlichere und ganz friedliche Anwendungen, beispielsweise in der Materialwissenschaft). Wir wählen also immer zufällig ein Feld aus und ändern die Zahl in diesem Feld nach bestimmten Regeln, die sicherstellen, dass am Ende die korrekte Thermodynamik herauskommt. (Wenn ihr die Regeln wissen wollt, könnt ihr ja mal mein Vorlesungsskript (Kap. 7) lesen – das pdf ist sogar kostenlos…) Dabei bestimmt, wie gesagt, die “Temperatur”, wie die Wahrscheinlichkeiten genau verteilt sind.
Wendet man so einen Algorithmus auf das Sudoku an, so verändert es sich also ständig. (Dabei ist es wichtig, dass die Hinweisfelder nicht verändert werden dürfen, sondern “eingefroren” bleiben.) Mal hat es Zustände mit hoher, mal mit niedrigerer Energie.Nach dem, was ich bisher geschrieben hab, könntet ihr annehmen, dass sich das Sudoku die meiste Zeit in dem Zustand der korrekten Lösung aufhält, denn der hat ja die niedrigste Energie (Null) und ist deshalb am wahrscheinlichsten. So ist es aber nicht, denn in einem eindeutigen Sudoku (das also nur eine Lösung hat) gibt es nur einen einzigen solchen Zustand, aber Millionen oder gar Milliarden andere mit höherer Energie. Nur bei extrem niedrigen Temperaturen “gewinnt” der Lösungszustand, wenn die Temperatur höher ist, dann findet man das Sudoku meist in einem Zustand mit mehr oder weniger vielen Fehlern, weil es davon einfach so viele gibt.
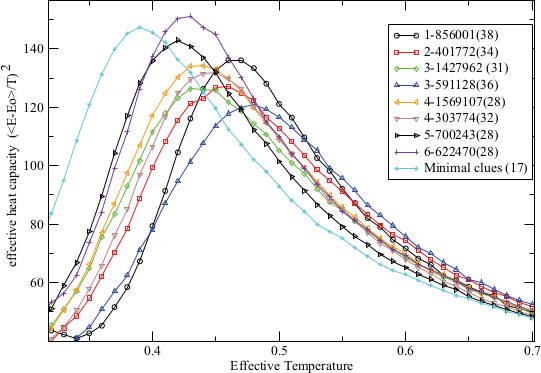
Weil unser Sudoku nun ein physikalisches System geworden ist, so richtig mit Energie und allem, kann man auch seine Eigenschaften angucken. Beispielsweise kann man (im Computer) messen, wie viel Energie das Sudoku schluckt, wenn man die Temperatur erhöht. Das nennt man die Wärmekapazität – genau wie bei normalen Materialien, bei denen man auch Energie reinstecken muss, um die Temperatur zu erhöhen (bei Wasser zum Beispiel eine Kalorie, um ein Gramm um ein Grad zu erwärmen). (Wobei die “Energie” beim Sudoku ja die Zahl der Fehler ist – man guckt sich also an, wie sich die Zahl der Fehler mit der Temperatur ändert und verrechnet das dann zur Wärmekapazität.) Die Wärmekapazität des Sudokus sieht (für unterschiedliche Fälle, also unterschiedliche Hinweiszahlen) so aus:
Aus Williams and Ackland, s.u.
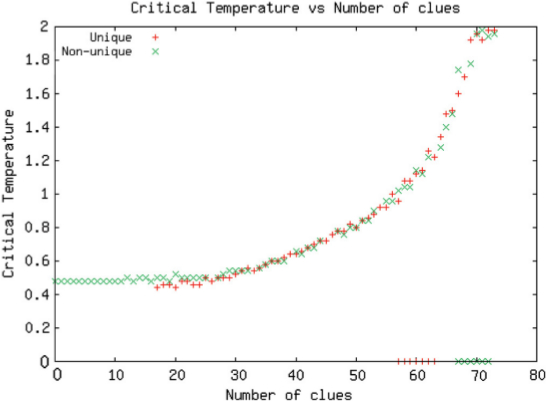
Bei niedrigen Temperaturen ist sie klein, dann steigt sie auf einen Maximalwert an, um dann wieder abzufallen. Die unterschiedlichen Kurven stehen dabei für unterschiedliche Sudokus (also unterschiedliche festgehaltene Hinweisfelder). Tendenziell zeigt sich, dass das Maximum weiter links liegt (also bei niedrigeren Temperaturen), wenn das Sudoku wenige ausgefüllte Hinweisfelder hat (die Zahl in Klammern), und weiter rechts bei vielen ausgefüllten Hinweisfeldern. Das zeigt dieses Bild noch einmal genauer:
Aus Williams and Ackland, s.u.
Wobei hier die kritische Temperatur (also die des Maximums) gegen die Zahl der Hinweise aufgetragen ist. (Die beiden Datenpunktreihen unterscheiden sich darin, dass bei der einen die Lösung eindeutig ist, bei der anderen nicht. Sudokus mit eindeutiger Lösung müssen mindestens 17 Hinweise enthalten.)
Was lernt man nun aus einer solchen Kurve? PhysikerInnen können über das obere Diagramm der Wärmekapazität in Entzücken geraten – es deutet nämlich auf einen Phasenübergang hin. Phasenübergänge kennt ihr alle aus dem Alltag (wenn auch vielleicht nicht unter diesem Namen): Wasser gibt es zum Beispiel in einer flüssigen und einer festen Phase, und wenn man es abkühlt, dann gefriert es irgendwann – das ist genau ein Phasenübergang. Wenn die Kurve der Wärmekapazität einen Knick oder Sprung hat, dann kann man ziemlich sicher sein, dass man es mit einem Phasenübergang zu tun hat. (Anmerkung für die ExpertInnen: Das Maximum ist hier nicht scharf, weil unser Sudoku ja nur eine endliche und ziemlich kleine Größe hat.)
In unserem Sudoku ist die Hochtemperaturphase eine, bei der vergleichsweise viele Fehler im Sudoku sind, so dass die Energie hoch ist. Die Niedrigtemperaturphase (eigentlich sind es zwei, dazu später mehr) ist dagegen eine, bei der die meisten Felder korrekt ausgefüllt sind, es aber an einigen Stellen nicht stimmt. Sudokus (insbesondere schwierige) haben oft scheinbar sehr viele Möglichkeiten, die Felder auszufüllen, und es gibt nur wenige Stellen im Sudoku, an denen es am Ende zu einem Fehler kommt. So eine “Fast-Lösung” kann aber trotzdem ganz anders aussehen als die richtige Lösung – genau das macht Sudokus ja so knifflig (wie wir noch sehen werden, kann man das sogar quantifizieren).
Eine “Fast-Lösung” hat – weil ja die meisten Felder passen – eine niedrige Energie. Um von diesem Zustand mit niedriger Energie zur korrekten Lösung zu kommen, muss man aber sehr viele Felder ändern – tut man dies Schritt für Schritt, wie der hier verwendete Simulationsalgorithmus, so führt der Weg von einem Zustand niedriger Energie zu einem anderen über lauter Zustände mit hoher Energie, die bei niedrigen Temperaturen sehr unwahrscheinlich sind. Das System ist dann in der “Fast-Lösung” gefangen. Weil die Energie hier besonders niedrig ist (wenn auch nicht Null) spricht man auch von einem “lokalen Minimum”.
So etwas gibt es auch in anderen Systemen mit einem Phasenübergang. Eisen beispielsweise wird bei niedrigen Temperaturen (unterhalb 768°C) magnetisch – in der Schule habt ihr vermutlich gelernt, dass es da “Elementarmagnete” gibt (was auch als Modell ganz brauchbar ist). Energetisch am günstigsten wäre es, wenn alle Elementarmagnete überall in dieselbe Richtung zeigen werden, aber beim Abkühlen passiert das normalerweise nicht, weil unterschiedliche Bereiche im Eisen unterschiedliche Ausrichtungen haben. Unser Sudoku benimmt sich also tatsächlich wie ein physikalisches System.
Betreibt man das Sudoku bei niedriger Temperatur, dann fällt es schnell in so ein lokales Minimum und bleibt darin. Erhöht man die Temperatur, dann verbringt es immer noch viel Zeit innerhalb der Zustände mit kleiner Energie, kann aber zwischen diesen hin- und herwechseln. Bei solchen mittleren Temperaturen befindet sich das Sudoku deshalb auch oft um Zustand mit der kleinsten Energie, also im Zustand der korrekten Lösung. Hier seht ihr, wie viel Zeit das System im Zustand der korrekten Lösung verbringt, wenn man unterschiedliche Temperaturen einstellt:
Aus Williams and Ackland, s.u.
Bei ganz niedrigen Temperaturen sind wir in einem fast richtigen Zustand gefangen (dass man tatsächlich die Lösung erwischt, ist sehr unwahrscheinlich), bei mittleren Temperaturen wechseln wir zwischen Zuständen mit niedriger Energie und sind deshalb auch oft im Lösungszustand, bei hohen Temperaturen findet man den Lösungszustand auch nahezu nie vor, weil die anderen falschen Zustände ja dann fast genauso wahrscheinlich sind.
Wenn ihr die Temperaturskala mit der im Bild oben vergleicht, dann seht ihr, dass der Phasenübergang, den wir oben bei der Wärmekapazität entdeckt haben, etwas oberhalb von der Temperatur stattfindet, bei der das Sudoku die maximale Zeit im Zustand der korrekten Lösung verbringt. Es gibt also drei Phasen: Die Hochtemperaturphase, in der sehr viele Fehler auftreten, die Phase bei mittlerer Temperatur, in der das Sudoku meist in einem lokalen Minimum ist, aber zwischen diesen Minima hin- und herwechseln kann, und dann die Niedrigtemperaturphase, bei der das System in einem lokalen Minimum eingefroren ist. Die drei Phasen werden – wegen unterschiedlicher Analogien zu anderen physikalischen Systemen – auch als “paramagnetische Phase”, “kondensierte (oder feste) Phase” und “Glasphase” bezeichnet.
Durch Variation der Temperatur kann man den Algorithmus übrigens auch tatsächlich zum Lösen von Sudokus verwenden. Das ist allerdings nicht besonders effizient – es gibt wesentlich bessere Möglichkeiten zum Lösen von Sudokus. An dem Bild seht ihr aber noch etwas anderes: Die unterschiedlichen Sudokus unterscheiden sich in der Zahl der vorgegebenen Hinweise (die Nummer in Klammern) und auch in ihrem Schwierigkeitsgrad – das ist jeweils die erste Zahl vor dem Strich. (Der Schwierigkeitsgrad wird dabei, wenn ich es richtig verstehe, darüber festgelegt, welche Schlussfolgerungstechnik man zum Lösen anwenden muss.) Ihr seht also, dass schwierige Sudokus auch als thermodynamische Systeme betrachtet weniger gern im Grundzustand sind als einfache – die Schwierigkeit für den Menschen korreliert zumindest einigermaßen mit dem thermodynamischen Verhalten.
Ist das alles denn auch zu irgendetwas gut? Ja, das ist es: Komplexe thermodynamische Systeme zu verstehen, ist nicht einfach. PhysikerInnen sind deshalb immer auf der Suche nach Modellsystemen, an denen sie ihre Ideen testen können. Das Sudoku-System ist einerseits erstaunlich einfach, zeigt aber mit seinen vielen lokalen Minima bei niedrigen Temperaturen und dem doppelten Phasenübergang ein ziemlich reichhaltiges Repertoire an thermodynamischen Phänomenen. Es ist also damit zu rechnen, dass das System in Zukunft noch weiter erforscht wird – und zusätzlich hat es den Vorteil, das Physik-DoktorandInnen in Zukunft immer behaupten können, dass sie Wissenschaft betreiben, wenn sie mit einem Sudoku-Heft erwischt werden.
A Williams and G. J. Ackland
Paramagnetic and glass transitions in sudoku
PHYSICAL REVIEW E 86, 031109 (2012)







Kommentare (10)