Dass die Raumzeit gekrümmt ist, ist ja gewissermaßen der Kern der Allgemeinen Relativitätstheorie. Im ersten Teil dieses Artikels habe wir allerdings gesehen, dass die Interpretation dieser Aussage nicht unbedingt eindeutig ist – wir können uns den “gekrümmten Raum” auch anders vorstellen, nämlich als ein Feld, das in einem ungekrümmten Raum lebt, aber alle Maßstäbe “in genau gleicher Weise” verzerrt. Eigentlich sollte ich jetzt etwas über die Zeit schreiben, aber das muss noch etwas warten. Ich habe nämlich gerade gemerkt, dass das “in genau gleicher Weise” arg missverständlich ist. (Jedenfalls habe ich gestern gemerkt, dass ich es immer etwas missverstanden habe.) Deshalb gucke ich heute noch etwas genauer hin, was das eigentlich bedeuten soll.
Warnung: Wie so oft, wenn ich versuche, mir physikalische Theorien zu veranschaulichen, habe ich mir die meisten Beispiele und Überlegungen hier selbst zusammengebastelt. Ich übernehme deswegen wie üblich keine Garantie, dass alles stimmt – falls jemand Fehler entdeckt, hinterlasst einen Kommentar. Ansonsten habe ich keine Ahnung, ob diese Überlegungen hier eurer Anschauung auf die Sprünge helfen oder alles nur unnötig verkomplizieren – mir hat der Gedankengang hier jedenfalls ziemlich weitergeholfen.
Schauen wir nochmal auf unsere Platte mit dem Temperaturfeld vom letzten Mal:
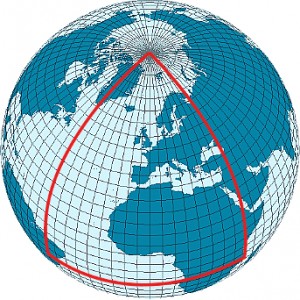
Stellt euch vor, ihr seid am “Äquator” (also in der Mitte der Platte im blauen Bereich) und nehmt zwei Kugeln, die ihr genau nach Norden rollt. Wenn ihr das tut, stellt ihr fest, dass sich die beiden Kugeln annähern, weil sich eure Maßstäbe ja auf dem Weg nach Norden wegen der höheren Temperatur verlängern. Im Bild der Kugeloberfläche ist das natürlich vollkommen klar – ich recycle mal ein älteres Bild:
Zwei Kugeln, die am Äquator parallel zueinander nach Norden losrollen, treffen sich schließlich am Nordpol. Auf der Oberfläche einer Kugel gibt es ja keine parallelen Linien, die sich nie schneiden.
Als nächstes bohren wir jeweils ein Loch in die Kugeln und schieben sie auf einem starren Draht, so dass sie auf dem Draht reibungsfrei gleiten können (ich weiß, in der SRT gibt es keine unendlich starren Materialien, wir nehmen erst mal das steifste und festeste Material, das wir bekommen können, meinetwegen Ynkelonium-Terkonit, kurz Ynketerk). Jetzt nehmen wir die ganze Konstruktion (Draht mit Kugeln drauf) und schieben sie kräftig vom Äquator aus nach Norden an. Was wird passieren?
Im Kugel-Bild ist das leicht zu sehen: Die Kugeln näher sich einander an, genau wie vorher – da der Draht starr ist, passiert ihm scheinbar nichts, so dass die Kugeln auf dem Draht nach Innen gleiten. Im Bild mit dem Temperaturfeld bewegen sich die Kugeln senkrecht nach oben im Bild – der Stab aber dehnt sich immer weiter aus, so dass die Kugeln nach innen gleiten. Nach wie vor können wir die beiden Situationen nicht unterscheiden.
Als nächstes machen wir die Sache etwas realistischer: Die Kugeln gleiten nicht mehr ganz reibungsfrei, sondern schubbern auf dem Draht entlang. Dann werden die Kugeln nicht mehr genau ihrer Bahn nach Norden folgen, sondern etwas seitlich abgelenkt, so dass der Abstand zwischen ihnen größer wird als vorher. Umgekehrt üben die Kugeln eine Kraft auf den Draht aus (was diesem nichts macht, weil er ja aus Ynkelonium-Terkonit ist, so dass er sich praktisch nicht verformt.)
Jetzt machen wir die Sache noch etwas realistischer: Der Draht ist aus einem gewöhnlichen Material, beispielsweise Aluminium. Die Kugeln, die auf dem Draht reiben, üben jetzt eine Kraft auf den Draht aus, der diesen daran hindert, sich so auszudehnen, wie er es “eigentlich” tun möchte. Verglichen mit unserem Ynkelonium-Terkonit-Draht wird also der Alu-Draht auf seinem Weg nach Norden etwas kürzer sein, weil die Kugeln ihn am Ausdehnen hindern (jedenfalls in dem Bereich zwischen den Kugeln). Im Extremfall können wir auch sehr schwere Kugeln nehmen und sie am Ende des Drahtes festkleben, dann drücken die Kugeln den Draht richtig zusammen. (Anmerkung: Wenn ihr euch das im Bild der Erdkugel vorstellen wollt, dann geht das vielleicht am besten, wenn ihr annehmt, dass die Kugeln und der Draht auf einer Umlaufbahn um die Erde kreisen – die Bahnen von zwei Satelliten, die anfänglich parallel laufen, kreuzen sich irgendwann, also gibt es zwischen ihnen eine Kraft.)







Kommentare (23)