Im ersten Teil des Artikels haben wir gesehen, dass man die Gleichung E=mc² folgendermaßen interpretieren kann: Wenn ein Objekt vor uns liegt, dann können wir ihm Energie entziehen. Tun wir das, dann veringert sich die Masse des Objekts, und zwar genau um den Betrag, den die Gleichung angibt. Umgekehrt erhöht sich die Masse, wenn wir dem Objekt Energie zuführen.
Kniffliger (und etwas verwirrend) wird die Sache, wenn Objekte sich bewegen.
Nach der Relativitätstheorie ist es ja unmöglich, dass Objekte (wie etwa Schokoladentafeln) sich mit Lichtgeschwindigkeit bewegen. Was passiert also, wenn man ein Objekt immer weiter beschleunigt? Zum Beschleunigen braucht man ja eine Kraft, und nach dem zweiten Newtonschen Gesetz (das ich hier ausführlich erklärt habe) ist die Beschleunigung (also die Änderung der Geschwindigkeit) gleich der Kraft geteilt durch die Masse. Wenn ein Objekt immer schneller wird, dann kann ich es aber irgendwann nicht mehr wesentlich weiter beschleunigen, weil die Lichtgeschwindigkeit ja eine Grenze darstellt, die man nicht erreichen kann. Wenn die Schokoladentafel sich mit sehr niedriger Geschwindigkeit bewegt, dann bekomme ich mit einer Kraft von 1 Newton eine Beschleunigung von 10m/s² (F=ma, also a=F/m= 1Newton/0,1kg=10m/s²); wirkt die Kraft also für eine Sekunde, wird die Tafel um 10m/s schneller.
Nehmen wir an, die Tafel Schokolade bewegt sich jetzt fast mit Lichtgeschwindigkeit (die hat den Wert 299792458m/s), sagen wir, mit einer Geschwindigkeit, die nur 1m/s kleiner ist als die Lichtgeschwindigkeit (also 299792457m/s). Wenn ich jetzt die Kraft 1 Newton für eine Sekunde wirken lasse, dann kann ich die Schokolade nicht um 10m/s beschleunigen, denn dann wäre sie überlichtschnell. Die tatsächliche Beschleunigung, die ich bekomme, ist deshalb viel kleiner.
Man kann das experimentell übrigens nachweisen – nicht mit Schokoladentafeln, aber zum Beispiel in Teilchenbeschleunigern. Wenn am LHC Protonen aufeinanderprallen, dann haben sie eine Energie von 7 Teraelektronenvolt (das ist eine Energieeinheit der Hochenergiephysik – es ist etwas mehr als das 7000fache der Masse des Protons, wenn man die Gleichung E=mc² verwendet). Nach den Regeln der klassischen Physik müssten sie mit dieser Energie etwa das 120fache der Lichtgeschwindigkeit erreichen – das tun sie aber nicht; ihre Geschwindigkeit ist immer knapp unterhalb der Lichtgeschwindigkeit. (Die Geschwindigkeit wird im LHC tatsächlich gemessen, weil man ja weiß, wann die Teilchen bei den jeweiligen Detektoren ankommen.) Man übt eine Kraft auf die Protonen aus, nicht um sie noch weiter zu beschleunigen, sondern um ihren Energiegehalt zu erhöhen, auch wenn sich die Geschwindigkeit nur noch minimal ändert.
Nähert man sich der Lichtgeschwindigkeit immer weiter, wird es also immer schwieriger, ein Objekt noch zu beschleunigen. In der Anfangszeit der Relativitätstheorie hat man das so ausgedrückt, dass man gesagt hat “O.k., da wir die Gleichung F=ma haben, und da wir bei gleicher Kraft immer weniger Beschleunigung bekommen, nimmt die Masse eines Objekts zu, je schneller es sich bewegt.” Das ist der berühmte relativistische Massezuwachs.
Allerdings wird die Sache dadurch komplizierter, dass das Ganze auch von der Richtung abhängt, in der die Kraft wirkt. Ist die Kraft in Richtung der Geschwindigkeit orientiert, dann ist der relativistische Massezuwachs größer als bei einer Kraft, die senkrecht zur Bewegungsrichtung ist (zum Beispiel, wenn das Teilchen auf einer Kreisbahn umläuft und ihr die Kraft betrachtet, mit der das Teilchen auf der Kreisbahn gehalten wird). Deswegen hat man zwischen “longitudinaler” und “transversaler” relativistischer Masse unterschieden. Details dazu könnt ihr zum Beispiel hier nachlesen. (Dort wird allerdings behauptet, man könne direkt aus dem Konzept der relativistischen Masse die Gleichung E=mc² ableiten. Das halte ich für falsch, aber dazu gibt es demnächst einen Extra-Text.) Noch komplizierter wird es, wenn die Kraft in irgendeinem beliebigen Winkel zur Bewegungsrichtung angreift – dann ist die Beschleunigung nicht mehr parallel zur Kraft. (Mathematisch müsste man die Masse durch einen Tensor beschreiben.)
Ein Vorteil, den das Konzept der “relativistischen Masse” (wenn man die transversale Masse nimmt) hat, ist der, dass es damit einfach ist, die Energie eines Objekts auszudrücken. Ein bewegtes Objekt hat ja eine Bewegungsenergie. Verwendet man die relativistische Masse, dann gilt aber wie vor die Gleichung E=mc² – wenn sich das Objekt bewegt, müsst ihr nur die relativistische Masse einsetzen. (Für kleine Geschwindigkeiten kommt dann für die kinetische Energie genau die Formel (1/2) mv² heraus, die ihr vielleicht mal in der Schule gelernt habt.)
Dieses Bild hier zeigt, wie die (transversale) Masse mit der Geschwindigkeit – scheinbar – zunimmt, das Symbol γ (gamma) gibt den Faktor an, um den die Masse wächst.
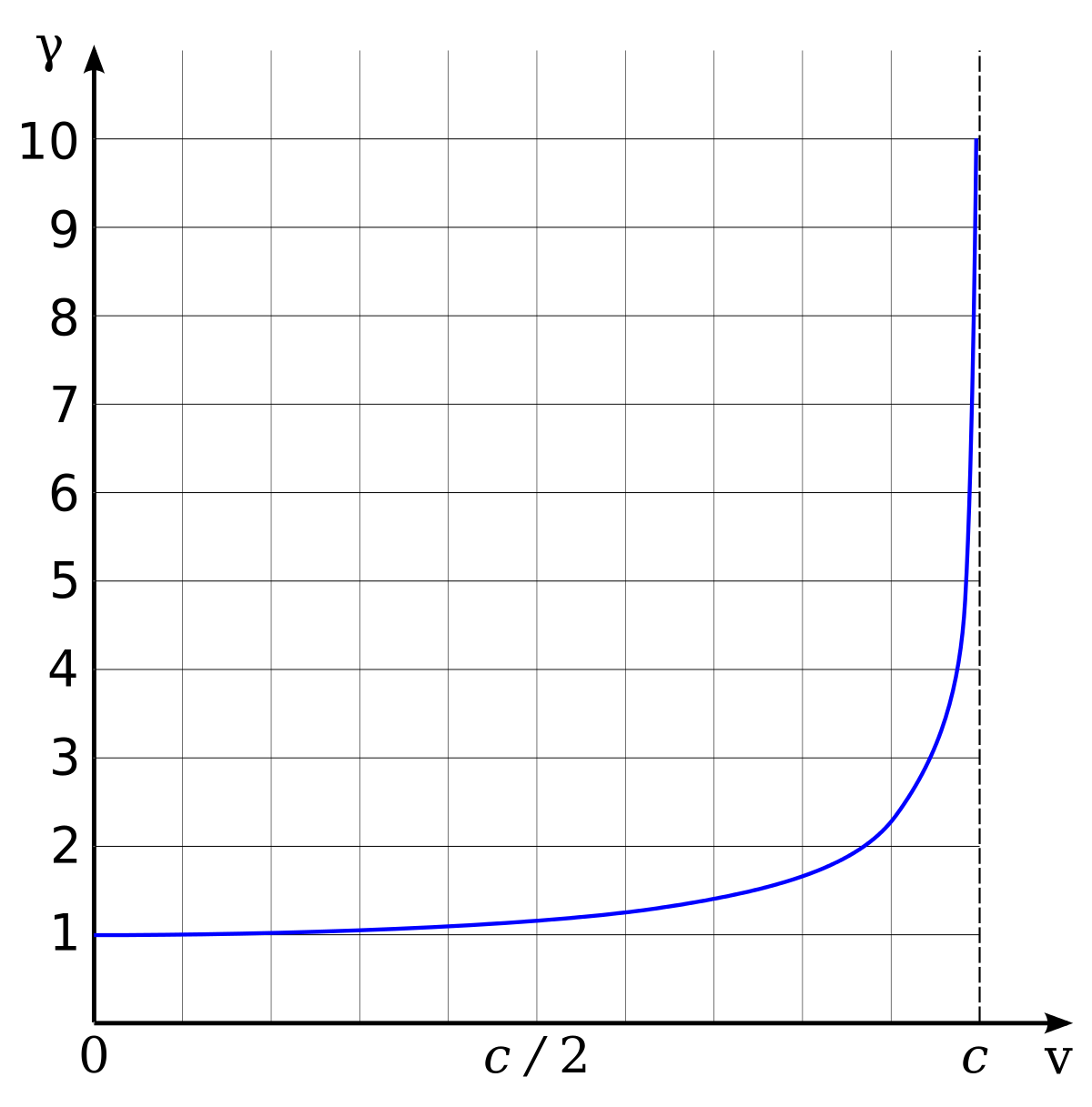
Von egg, Graph created with KmPlot, edited with Inkscape Trassiorf (talk) 21:54, 2 March 2010 (UTC) – Eigenes Werk, Gemeinfrei, https://commons.wikimedia.org/w/index.php?curid=2868331
Übrigens: Falls ihr den Massebegriff etwas verwirrend findet, liegt das daran, dass er verwirrend ist. Ich habe das vor längerer zeit in diesem Artikel auseinandergedröselt. Da habe ich übrigens mal “Masse ist Energie” geschrieben – in dem Zusammenhang dort war das wohl o.k., abr ein bisschen Vorsicht ist mit der Aussage schon geboten. In dem Artikel habe ich übrigens in Sachen relativistischer Masse etwas falsch argumentiert, weil ich das mit der logitudinalen und transversalen Masse nicht ganz richtig auf der Reihe hatte – ich habe die entsprechende Stelle aber gerade mit einer Anmerkung versehen.






Kommentare (22)