Das Higgs-Teilchen ist ja immer für Verwirrung gut. Das liegt sicher auch daran, dass anschauliche Erklärungen des Higgs-Mechanismus, der ja bekanntlich anderen Teilchen ihre “Masse verleiht” alle irgendwie etwas hinken. Manchmal wird das Higgsfeld mit einer Art Honig verglichen, manchmal werden Prominente auf Partys gescheucht, und ich habe mich auch schon mal mit einer anschaulichen Erklärung schwergetan.
Das Hauptproblem bei all diesen anschaulichen Erklärungen ist, dass sie schnell zu Widersprüchen führen. Wäre Das Higgsfeld wie Honig, dann würden alle Teilchen ja irgendwann zur Ruhe kommen. Das Party-Beispiel ist soweit weg von echter Physik, dass man in ihm eigentlich fast gar nichts mehr weiterdenken oder verstehen kann.
Schön wäre also eine Erklärung des Higgs-Mechanismus, die einigermaßen anschaulich ist, aber trotzdem zumindest die wichtigsten Eigenschaften beibehält, so dass man zumindest ein bisschen innerhalb des anschaulichen Modells weiterdenken kann. (Zum Thema Anschauung empfehle ich auch diesen Blogartikel.)
Ich bemühe mich mal, den Haupttext schön einfach zu halten – aber ab und zu baue ich vertiefte Erklärungen ein, die ihr sehen könnt, wenn ihr mit der Maus über die Sternchen fahrt, so wie dieses hier: * Ich nehme ein Sternchen für Erklärungen, die meiner Ansicht nach einigermaßen für alle verstehbar sind, zwei Sternchen für abgefahrenes Zeugs mit Mathematik und so…
Das Problem mit all diesen Erklärungen ist, dass sie Elementarteilchen wie Elektronen als Teilchen beschreiben, also wie kleine, genau lokalisierbare Kugeln. Tatsächlich verhalten sich Elementarteilchen aber in vieler Hinsicht eher wie Wellen als wie Teilchen (das steckt ja auch hinter dem berühmten Welle-Teilchen-Dualismus)*. Deshalb ist es viel besser, sich den Higgs-Mechanismus mit Hilfe von Wellen zu veranschaulichen.
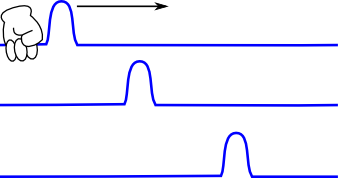
Stellt euch ein gespanntes Seil vor, bei dem ihr an einem Ende des Seils zupft. Es breitet sich eine Störung (eine Erschütterung des Seils ich spüre…) entlang des Seils aus, die mit konstanter Geschwindigkeit weiterwandert (jedenfalls in einem idealen Seil, in dem es keine Reibung und sonstige störenden Effekte gibt). **
Egal wie ihr zupft, die Geschwindigkeit der Seilwelle ist immer dieselbe – sie hängt davon ab, wie schwer das Seil ist und aus welchem Material es ist, aber die Feinheiten sind mir im Moment noch egal **. In einem idealen Seil würde die Welle (vornehm sollte man von einem “Wellenpaket” sprechen, ein Beispiel für so ein Paket seht ihr auch in meinem Blogheader oben) auch nicht auseinanderlaufen, sondern ihre Form beibehalten. Betrachtet ein solches “Wellenpaket” als ein Teilchen.**
Wie gesagt ist die Geschwindigkeit eines solchen Wellenpakets (also des “Teilchens”) immer dieselbe. Das Wellenpaket kann nicht langsamer oder schneller werden, es hat immer dieselbe Geschwindigkeit. Na, erinnert euch das an etwas?
Richtig: Licht breitet sich auch immer mit derselben Geschwindigkeit aus. (Wobei für unsere Seilwelle natürlich keine Relativitätstheorie oder so gilt, aber das dürfen wir ignorieren, wir sind immer relativ zum Seil in Ruhe.) Unsere Teilchen entsprechen also Teilchen, die sich mit Lichtgeschwindigkeit ausbreiten, so wie es Elementarteilchen wie Elektronen tun würden, wenn es kein Higgsfeld gäbe. *
Was tut das Higgsfeld? Um das zu sehen, müssen wir eine wichtige Eigenschaft unseres Seils verstehen: Stellt euch ein sehr, sehr, sehr (also wirklich seeehr) langes Seil vor (wenn ihr genug Fantasie habt, stellt es euch unendlich gleich lang vor). Wenn ich jetzt das ganze Seil ein wenig nach oben oder unten auslenke, dann passiert – nichts. Die Schwingung im Seil kommt ja daher, dass das Seil gedehnt wird und das Material im Seil sich wieder zusammenzieht (weil man eine Kraft braucht, um das Seil zu dehnen). Eine Auslenkung des ganzen Seils verschiebt das Seil aber, ohne es zu dehnen. (Das ist übrigens auch der Grund, warum masselose Teilchen wie Photonen beliebig kleine Energien haben können.) **
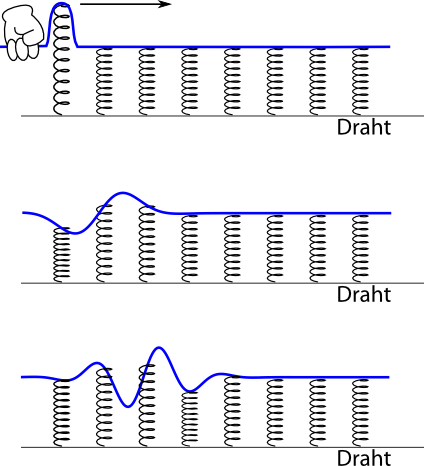
Genau an dieser Eigenschaft des Seils dreht das Higgsfeld. Anschaulich könnt ihr euch vorstellen, dass es neben dem Seil noch einen Draht gibt. Der Draht ist so unglaublich fest, dass er nicht gedehnt werden kann. Zwischen dem Draht und unserem Seil spannen wir überall kleine Federn oder Gummibänder *:
Starten wir wieder mit einem Wellenpaket. Da wo das Seil stark ausgelenkt ist, gibt es eine starke rücktreibende Kraft, weil die Federn das Seil ja zurückziehen.** Und was passiert, wenn man etwas an einer Feder befestigt und dann die Feder auslenkt? Richtig, es schwingt auf und ab. Unser Wellenpaket wird sich also nicht einfach ausbreiten, sondern es wird zumindest teilweise auch am aktuellen Ort für eine Auf- und Abschwingung sorgen. Wenn ihr das Wellenpaket anstoßt, so dass es in eine Richtung läuft, sorgt jetzt das Schwingen an den Federn dafür, dass das Wellenpaket gebremst wird. Das Wellenpaket läuft jetzt also mit einer kleineren Geschwindigkeit. ** So etwa sieht das Ergebnis aus:*
Jede Auslenkung des Seils, egal wie sie aussieht, kostet jetzt Energie, weil die Federn gedehnt werden.
Unser Wellenpaket bewegt sich jetzt also langsamer als vorher – die zusätzliche Energie, die die Federn zum Dehnen brauchen, ändert die Ausbreitung der Wellen. ** Genauso funktioniert auch der Higgsmechanismus: Das Higgsfeld entspricht im Modell hier den Federn. Es sorgt dafür, dass es immer Energie kostet, an einem Ort ein Teilchen ** zu haben, unabhängig von der Wellenlänge des Wellenpakets. (Während bei masselosen Teilchen, wie oben, ein Wellenpaket mit sehr langer Wellenlänge um so weniger Energie braucht, je größer die Wellenlänge ist.)
Das Higgsfeld bremst Teilchen also nicht direkt (so wie in der Veranschaulichung mit dem Honig), sondern es beeinflusst die Welleneigenschaften der Teilchen dadurch, dass es immer Energie kostet, irgendwo ein Teilchenfeld anzuregen. Dadurch wird eine laufende Welle verzögert und bewegt sich nicht mehr mit Lichtgeschwindigkeit.
Die Energieerhöhung selbst funktioniert wie eine Art Abstoßung *: Da, wo das Higgsfeld ist, brauche ich Extra-Energie, um dort andere Teilchen zu haben. Dumm nur, dass das Higgsfeld überall ist – also brauche ich überall Extra-Energie, um ein Teilchen zu bekommen, und genau das ist die Masse der Teilchen (na klar, wegen E=mc²).
Unsere reale Welt ist natürlich dreidimensional – da ist das mit der Schwingerei natürlich schwer vorzustellen. In zwei Dimensionen geht’s, da könnt ihr euch ein elastisches Tuch vorstellen, aber in drei Dimensionen versagt unsere Anschauung, weil wir uns dann eine Schwingung in die vierte Dimension vorstellen müssten, damit das Bild passt. *
Die Erklärung hier hat in meinen Augen einen Vor- und zwei Nachteile. Die Nachteile sind offensichtlich: Die Geschichte mit dem Honig oder Berühmtheiten auf Partys kann man in einer Minute erzählen, dieser Text hier ist etwas länger (obwohl ich mich wirklich bemüht habe…). Und das Schwingen von Seilen mit Federn dran ist nichts, wofür wir eine direkte gute Intuition haben, insofern muss man ein bisschen mehr nachdenken, um die Effekte einzusehen.* Der Vorteil ist vielleicht nicht ganz so offensichtlich, aber in meinen Augen entscheidend: Die Analogie ist mathematisch gesehen exakt: Die Gleichung, die die Ausbreitung von masselosen und massiven Teilchen beschreibt, ist dieselbe Wellengleichung wie bei einer Seilwelle ohne bzw. mit den dranhängenden Federn oder Gummibändern. In der Quantentheorie kommen natürlich noch die Quanteneffekte hinzu (dazu hatte ich ja oben schon was gesagt), weil wir eben immer nur ganze Teilchen beobachten und weil wir eigentlich unsere Wellen noch mit Wahrscheinlichkeiten versehen müssten, wie das in der Quantenmechanik so üblich ist. ** Aber davon abgesehen stimmt die Analogie. Wenn ihr euch etwas im Bild der Seilwelle korrekt überlegt, dann sollte das also entsprechend auch für ein Teilchen im Higgsfeld gelten.
Hier zum Abschluss ein Beispiel, wie das aussehen kann: Die Energie, die im Seil selbst gespeichert ist, ist ja um so höher, je kürzer die Wellenlänge unseres Wellenpakets ist (weil sich bei einer kurzen Wellenlänge das Seil von einem Punkt zum nächsten ja stark dehnen muss), während die Energie durch die Federn nur von der Auslenkung des Seils am jeweiligen Punkt abhängt. Ist die Wellenlänge sehr lang, dann wird die Energie entsprechend durch die Federn dominiert ** Ist die Wellenlänge dagegen sehr kurz, dann spielen die Federn keine große Rolle mehr, der Großteil der Energie steckt in der Seilspannung und der Schwingung, die durch diese Spannung zu Stande kommt. Bei kurzen Wellenlängen erwartet man also, dass sich das Teilchen nahezu genauso verhält wie ohne die Federn – Teilchen mit kurzen Wellenlängen entsprechen also solchen mit einer sehr hohen Geschwindigkeit nahe der Lichtgeschwindigkeit. Und genau so ist es auch, beispielsweise wenn am CERN Protonen aufeinandergeballert werden.
Aber vielleicht ist die Erklärung ja auch schon zu abgehoben und hilft nicht wirklich weiter. Was meint ihr dazu? Seilwellen mit Federn, oder doch lieber Kugeln in Honig?
PS: Ihr dürft auch gern sagen, ob ihr die mouseover-Technik hilfreich oder eher unpraktisch findet. Klappt das überhaupt sinnvoll auf nem Tablet oder Handy?
PPS: Wenn ihr nen Linux-Rechner habt, könnt ihr auch das gute alte Programm xwaves von Mike Creutz verwenden, um euch die Wellen mit und ohne Masse anzuschauen. Das sollte auf jedem Linux-Rechner mit X11 und nem C-Compiler funktionieren, ganz ohne “configure-make-make install”-Hölle.
PPPS: Die Dispersionsrelation etc. für Seilwellen mit und ohne Federn findet man sehr schön in diesem Dokument erklärt.
Und da das mit den Sternchen anscheinend nicht so klappt, hier die Anmerkungen als Fußnoten, ich hoffe, das geht auch auf mobilen Geräten…
* Zu Anfang ein Hinweis: was ich hier erkläre ist nur der Mechanismus, mit dem das Higgsfeld den ‘normalen’ Materieteilchen Masse verleiht, also so Dingern wie Elektronen oder den Quarks aus denen Atomkerne bestehen. Der Mechanismus, mit dem die sogenannten Eichbosonen ihre Masse bekommen, geht etwas anders. Dazu könnt ihr in meinem oben verlinkten Artikel starten.
*Wobei das mit dem Welle-Teilchen-Dualismus eine knifflige Sache ist. Meist verhalten sich die Elementarteilchen wie Wellen, nur wenn wir sie zwingen, sich zu entscheiden (zum Beispiel, indem wir messen, ob das Elektron gerade ‘hier’ ist, dann messen wir eben immer ganze Elektronen an einem Ort, nie bloß einen Teil eines Elektrons.
** Wenn man sich ein unendlich langes Seil denkt und die Störung durch lokales Zupfen (also sehr eng begrenzt) hervorgerufen wird, dann läuft vom Ausgangspunkt aus eine Welle in beide Richtungen de Seils. In der Analogie zu einem quantenmechanischen teilchen läuft dessen Funktion auch in beide Richtungen – das ist in gewisser Weise ein Überlagerungszustand, den man durch Messen des teilchens an einem Ort kollabieren lassen könnte. (Naja, in der QFT ist es noch etwas komplizierter, weil die Auslenkung selbst proportional zum Quantenfeld ist, das selbst ja erst mal mit den Mitteln der klassischen Physik beschrieben wird und das dann quantisiert wird, so dass man für jede Feldkonfiguration eine Wahrscheinlichkeit angibt. Ich habe hierfür eine wahrhaft wunderbare Erklärung, doch ist dieses mouseover hier zu schmal, um sie zu fassen. Ihr findet die ausführliche Erklärung aber in meiner QFT-Serie.)
** Mathematisch ist aber das nette, dass die Seilwelle praktisch dieselbe Lagrangefunktion hat wie ein (bosonisches) Quantenfeld: Es gibt einen Term für die kinetische Energie, proportional zum Quadrat der Zeitableitung, einen Term für die Energie der Seildehnung, proportional zum Quadrat der Ortsableitung. Beim idealen Seil ist deshalb die Frequenz proportional zur Wellenlänge, entsprechend ist die Wellengeschwindigkeit für alle Wellen gleich. (Und die Gruppen- und Phasengeschwindigkeit sind auch gleich.)
**Damit es wirklich ein Teilchen ist, müsst ihr die Gesamtauslenkung des Seils passend normieren, also so, dass das Integral über das Quadrat der Auslenkung gleich 1 ist.
*Vorsicht: Man muss sorgfältig zwischen dem Higgsfeld und dem Higgsteilchen unterscheiden: Das Higgsfeld ist ein Feld, dass das gesamte Universum überall gleichermaßen ausfüllt. Dieses Feld ist verantwortlich für den Higgsmechanismus. Man kann diesem Feld Energie zufügen und es so anregen, dann entsteht ein Higgs-Teilchen. Wenn man ein Higgs-Teilchen nachweisen kann (hat man ja inzwischen getan), dann ist das ein Beleg dafür, dass es auch das Higssfeld gibt.
** Denn in der Lagrangefunktion stecken ja nur Ableitungsterme. Das habe ich übrigens vor langer Zeit in meiner Quantenfeldtheorieserie (klickt rechts bei den Artikelserien) im Teil ‘Was sind Felder’ erklärt.
* Technisch ist das etwas trickreich, weil unser Seil nach wie vor frei nach oben und unten schwingen soll. Wenn euch das Sorgen macht, denkt euch zwei Drähte, einen oberhalb, einen unterhalb unseres Seils, die beide mit Federn mit unserem Seil verbunden sind.
** Weil es ein Gummiband oder eine Feder ist, ist die rückstellende Kraft proportional zur Auslenkung, die Energie ist dann proportional zum Quadrat der Auslenkung. Passt zum Masseterm in der Lagrangefunktion eines Quantenfeldes.
** Zusätzlich wird das Wellenpaket dabei auch noch breiter – es behält nicht, wie vorher, seine Form bei, sondern es ‘zerläuft’. In der Quantenmechanik könnt ihr das als eine Form der Unschärferelation ansehen – am Anfang ist der Ort des Teilchens einigermaßen gut bekannt, also ist seine Geschwindigkeit nicht ganz genau definiert, also muss das Wellenpaket mit der Zeit auseinanderlaufen. Mathematisch ist das aber schlicht eine Dispersionsrelation.”
* Das Bild istnur qualitativ zu verstehen, ich war zu faul, um die genaue Form des Wellenpakets nachzurechnen. Beachtet aber, dass die Spitze des Wellenpakets sich mit der gleichen Geschwindigkeit (eben der Lichtgeschwindigkeit) bewegt wie oben beim Seil ohne Federn, der Hauptteil ist aber deutlich verzögert.
** Und natürlich brauche ich generell mehr Energie, um das Seil überhaupt auszulenken – aber das ist auch richtig so, denn um ein massebehaftetes Teilchen zu erzeugen, brauche ich ja auch die zusätzliche Ruheenergie nach E=mc².
**Oder eine Wahrscheinlichkeit für ein Teilchen, bzw. eine Anregung des Quantenfelds, siehe auch die Bemerkung oben.
* allerdings nicht so wie zum Beispiel eine elektrische Abstoßung, denn es gibt hier keine Wirkung über eine Distanz: Das Higgsfeld erhöht die Energie nur da, wo sowohl Teilchen als auch Higgsfeld vorhanden sind, während sich elektrische Ladungen ja über eine Entfernung anziehen oder abstoßen.
* Noch ein wichtiger Hinweis: Teilchenfelder darf man sich natürlich nicht als Schwingungen in eine höhere Raumdimension vorstellen – das ist hier nur eine Veranschaulichung. Man zeichnet ja auch zum Beispiel elektrische Felder mit Pfeilen – die sind aber ja auch keine Pfeile, die irgendwo im Raum herumschwirren, sondern haben an jedem Ort im Raum einen Wert.
* Was nebenbei die Frage aufwirft, warum man in Quantenphysik-Vorlseungen nicht solche Seilmodelle mit und ohne Federn verwendet, um den Unterschied zwischen der Wellengleichung von Photonen und der Klein-Gordon-Gleichung für massive Teilchen zu veranschaulichen.
** Hinzu kommt auch noch, dass Teilchen wie Elektronen etwas komplizierter sind, weil die ja einen Spin haben.
** Mathematisch könnt ihr das sofort an Hand der Dispersionsrelation sehen: Es ist (bis auf unwichtige Vorfaktoren) ω = √(k²+m²). Für große Wellenlängen, also kleines k, ist ω (also auch die Energie) im wesentlichen gleich der Masse, für sehr großes k ist der Massenterm vernachlässigbar und es gilt näherungsweise ω~k, wie für ein masseloses Teilchen (oder die Seilwelle ohne Federn).







Kommentare (72)