Es ist schon wieder passiert, diesmal bei nature: Um die Eigenschaften des Vakuums zu beschreiben, wurde das alte Bild von Teilchen bemüht, die im Vakuum ständig entstehen und vergehen:
Empty space constantly bubbles with elementary particles that come into existence only to disappear moments later.
Man liest so etwas ja sehr oft, selbst auf seriösen Seiten wie dieser hier (die Erklärungen dort sind übrigens generell sehr gut) steht
In der Quantenfeldtheorie erscheint das Vakuum als ein dynamisches Medium, in dem ständig Teilchen-Antiteilchen-Paare entstehen und wieder verschwinden.
Obwohl diese Aussagen einen wahren Kern haben, suggerieren sie ein etwas falsches Bild. (Anmerkung: Ja, in meiner QFT-Serie oder meinen früheren Artikeln über das Vakuum (findet ihr, wenn ihr auf die Artikelserien klickt) habe ich den Vakuumzustand schon mal ausführlich erklärt, heute konzentriere ich mich auf das Bild selbst).
Was diese Beschreibungen suggerieren, ist, dass im Vakuum ständig etwas passiert: Wenn Teilchen und Antiteilchen entstehen und vergehen, dann habe ich vielleicht im Vakuum “hier” gerade ein Elektron, “dort” ein Photon, und einen Moment später ist das Elektron “hier” verschwunden und dafür habe ich jetzt “hier” ein Quark und ein anderes Elektron ist “dort” aufgetaucht. Der häufig verwendete Begriff “Quantenfluktuation” für diese Eigenschaft des Vakuums unterstützt dieses Bild ja auch.
Diese Vorstellung ist leider falsch. Das Vakuum hat zwei wichtige Eigenschaften: Es ist der Zustand mit der kleinst-möglichen Energie und es sieht für alle Beobachterinnen gleich aus (solange die nicht beschleunigt werden, sonst gibt es den sogenannten Unruh-Effekt, den ich kurz auch in meinem Buch erkläre – allerdings im Anhang. Hier bei Florian gibt es eine ähnliche Erklärung. Heute ignorieren wir den Unruh-Effekt aber.). Aus diesen beiden Eigenschaften kann man sich überlegen, dass das einfache Bild so nicht richtig sein kann.
Warum es so nicht sein kann
Wenn die Energie des Vakuums den kleinstmöglichen Wert hat, dann ist sie logischerweise konstant (denn warum sollte jetzt ein anderer kleinster Wert möglich sein als gleich?). Das Vakuum ist also ein Zustand, der eine ganz bestimmte Energie hat. (Das ist die berühmte “Nullpunktsenergie”, die man aber anders als in der Science Fiction nicht ohne weiteres anzapfen kann, weil es ja schon die kleinst-mögliche Energie ist.) Und jetzt schlägt eine Regel der Quantenmechanik zu: Ein Zustand mit konstanter Energie ist ein zeitlich unveränderlicher Zustand. In einem Zustand mit konstanter Energie passiert nichts, er sieht zu allen Zeiten genau gleich aus. Und wenn nichts passiert, dann können da auch keine Teilchen plötzlich auftauchen und wieder verschwinden.
Auch mit Hilfe der zweiten Vakuum-Eigenschaft können wir sehen, dass das mit den Teilchen-Antiteilchen-Paaren so einfach nicht sein kann. Nehmen wir an, es gäbe diese Paare. Dann können wir messen, wie viele solche auftauchenden und wieder verschwindenden Teilchen-Antiteilchen-Paare ich beispielsweise in einem bestimmten Moment in einem Kubikmeter Vakuum habe, die haben also eine bestimmte Dichte. Und dann nehmen wir uns ein Raumschiff und fliegen mit nahezu Lichtgeschwindigkeit an diesem Kubikmeter vorbei. Dank der Längenkontraktion der speziellen Relativitätstheorie sieht das Volumen jetzt kleiner aus. Also messe ich eine höhere Dichte an diesen Paaren als vorher, der Vakuumzustand sieht also für mich jetzt anders aus. Und genau das ist etwas, das das Vakuum nicht tun sollte, es muss für alle Beobachterinnen gleich aussehen. (Außer, wenn sie beschleunigen, weil es dann den oben erwähnten Unruh-Effekt gibt.)
Woher die Idee kommt
Aber wenn die Vorstellung falsch ist, warum ist sie dann so verbreitet? Ganz einfach: Sie hat einen wahren Kern. Um den zu sehen können wir beispielsweise die berühmten Feynman-Diagramme verwenden. In einem Feynman-Diagramm stellt man ja Prozesse dar, die sich mit irgendwelchen Elementarteilchen abspielen, beispielsweise so:
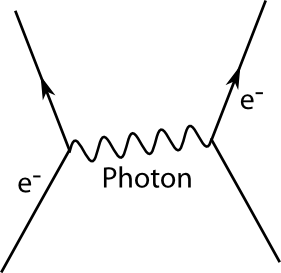
Hier sind zwei Elektronen unterwegs, tauschen ein Photon aus und ändern dabei ihre Richtung. (Die genauen Regeln, wie man solche Diagramme erstellt und benutzt, habe ich vor langer Zeit mal erklärt.) Die Zeitachse zeigt im Bild von unten nach oben, die horizontale Achse soll den gesamten dreidimensionalen Raum darstellen.
Wenn man den Vakuumzustand mit solchen Diagrammen beschreiben will, dann sieht das beispielsweise so aus:
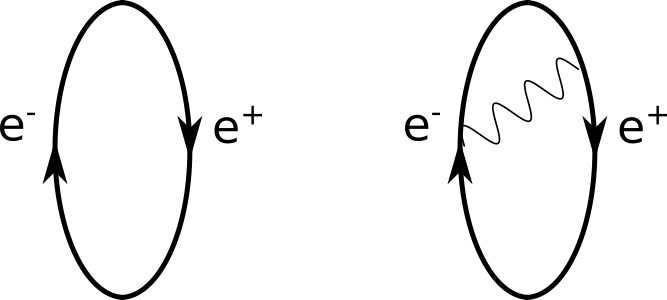
Hier entsteht links ein Paar aus einem Elektron und einem Positron quasi “aus dem Nichts” und verschwindet dann wieder. Im rechten Teilbild tauschen die beiden noch ein Photon miteinander aus.
“Aber ist das nicht genau das, was die angeblich falsche Erklärung sagt? Dann ist sie also doch richtig?” fragt jetzt die schlaue Blog-Leserin vollkommen zu Recht. Das Problem ist, dass Feynman-Diagramme nicht ganz so leicht zu interpretieren sind, wie es den Anschein hat. Nehmen wir nochmal das Diagramm von oben mit den beiden Elektronen, die ein Photon austauschen. Es sieht so aus, als würde das linke Elektron an einem bestimmten Punkt ein Photon aussenden, das dann vom rechten Elektron etwas später (die Zeit verläuft im Bild ja von unten nach oben) absorbiert wird. Aber das ist nicht die ganze Wahrheit. Das linke Elektron kann das Photon irgendwann aussenden, das rechte kann es irgendwann absorbieren. Und auch umgekehrt – es gibt keinen Grund, warum der Zeitpunkt, wo die Photon-Linie das rechte Elektron trifft, nicht vor den liegen sollte, wo sie das linke Elektron trifft, so dass das Photon dann vom rechten Elektron ausgesandt wird. Erst wenn man alle diese Möglichkeiten berücksichtigt, bekommt man eine korrekte Beschreibung des Prozesses.
Entscheidend ist also, dass man ein Feynman-Diagramm nicht einfach isoliert als einen Prozess betrachten darf: Man muss alle Möglichkeiten angucken, wie dieser Prozess stattfinden kann und alle diese Möglichkeiten gemeinsam betrachten. Erst wenn man über alle diese Möglichkeiten summiert, erhält man eine korrekte Beschreibung dessen, was passiert – ein konkreter Einzelfall allein mit einem bestimmten Ort für die Aussendung und Absorption des Photons hat für sich genommen keine Aussagekraft.
Für unser Vakuum bedeutet das, dass wir über alle denkbaren Orten und Zeiten, an denen die Teilchen entstehen und vergehen können, mitteln müssen. Damit ist dann alles wieder unabhängig von Ort und Zeit und unser Vakuumzustand sieht immer und überall gleich aus, so wie es sein muss.
Das Bild hat also durchaus einen wahren Kern, aber es verschweigt einen ganz zentralen Punkt.
Wie falsch ist das Bild?
Wenn das Bild von den ständig entstehenden und vergehenden Teilchen also einen wahren Kern hat, wie falsch ist es denn dann? Kann man es dann nicht doch verwenden?
Um das zu klären, schauen wir auf eine ähnliche Situation in der Quantenmechanik. Wir sperren beispielsweise ein Elektron in einen Kasten ein. Dann gibt es innerhalb des Kastens eine gewisse Wahrscheinlichkeit, das Elektron zu finden, etwa so (für den Zustand mit der niedrigsten Energie):
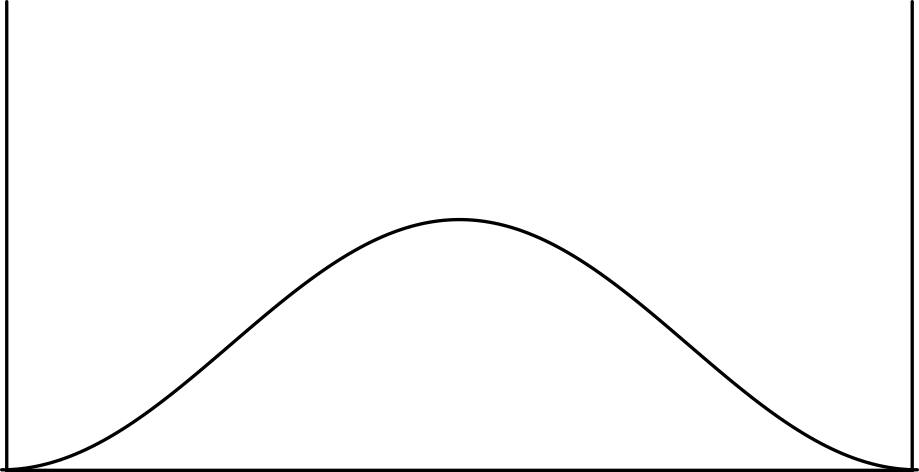
Aufgetragen ist dabei die Wahrscheinlichkeit (für Pingelige: Die Wahrscheinlichkeitsdichte), das Elektron zu finden – ganz am Rand des Kastens findet man es nicht, in der Mitte des Kastens findet man es mit einer besonders hohen Wahrscheinlichkeit.
Wir können uns diese Wahrscheinlichkeit (oder das zugehörige mathematische Objekt, die berühmte “Wellenfunktion” der Quantenmechanik) auch anders vorstellen, nämlich als eine Überlagerung aus unterschiedlichen Möglichkeiten. Das Elektron könnte an einem Ort irgendwo links sein, oder irgendwo in der Mitte oder rechts – jeden denkbaren Ort können wir mit der Wahrscheinlichkeit multiplizieren, das Elektron an diesem Ort zu finden. Das Gesamtbild bekommen wir, wenn wir alle diese Einzelorte zusammenfügen.
Damit ist die Situation jetzt vergleichbar mit der in den Feynman-Diagrammen oben: Auch dort musste man ja alle Möglichkeiten betrachten und erst die Gesamtheit aller Möglichkeiten beschreibt das Vakuum korrekt. Hier beim Elektron ist es genauso: Erst die Gesamtheit aller Möglichkeiten für den Ort beschreibt den Zustand des Elektrons korrekt.
Wenn man also sagt, dass im Vakuum ständig Teilchen entstehen und vergehen (ohne dazuzusagen, dass man alle diese Möglichkeiten gleichzeitig betrachten muss), dann ist das so, als würde man beim Elektron im Kasten sagen”Das Elektron ist mal hier und mal da”. Und das gibt dann natürlich schon ein falsches Bild dessen, was da passiert oder eben gerade nicht passiert, denn das Elektron ändert seinen Ort ja nicht, sondern hat eine bestimmte Aufenthaltswahrscheinlichkeit, die aber nicht von der Zeit abhängt.
Prozesse und Messungen
Nach dieser Überlegung ist das Bild des Vakuums mit Teilchen, die entstehen und vergehen, also schon wirklich ziemlich falsch. Allerdings kommt noch eine zusätzliche Komplikation hinzu. Ich erkläre sie erstmal am Elektron im Kasten. Nehmt an, wir würden den Ort des Elektron messen, beispielsweise indem wir irgendwo in der Mitte ein Photon einstrahlen, das dann mit dem Elektron wechselwirkt. Dann wissen wir, dass das Elektron an diesem Ort ist. (Das ist dann der berühmte Kollaps der Wellenfunktion, auch Messproblem genannt, der den Physikerinnen ziemliches Kopfzerbrechen bereitet, aber darüber habe ich schon anderswo geschrieben, deswegen führe ich das hier nicht aus.)
Wir finden in diesem Fall manchmal das Elektron an dem Ort, wo wir messen, manchmal auch nicht. (Und die Wahrscheinlichkeit dafür können wir dem Bild oben entnehmen.) Wenn wir jetzt die Wechselwirkung unseres Photons mit dem Elektron beschreiben und erklären wollen, warum das Photon das Elektron manchmal misst und manchmal nicht, dann können wir über die Wahrscheinlichkeiten argumentieren (und das wäre natürlich die beste Erklärung). Wir könnten aber auch sagen “So ein Elektron in einem Kasten ist manchmal hier, manchmal da, und je nachdem, wo es gerade ist, wird es vom Photon getroffen oder auch nicht.” Das stimmt nicht wirklich, wie wir ja eben gesehen haben, aber vielleicht kann man es als populärwissenschaftliche Erklärung trotzdem durchgehen lassen, je nachdem, wie genau man sein möchte.
Und genauso ist es auch mit dem Vakuum: Nein, im Vakuum entstehen nicht ständig irgendwo zufällig Teilchen und verschwinden wieder, aber wenn wir mit dem Vakuumzustand wechselwirken (beispielsweise bei Dingen wie der Vakuumpolarisation oder der populären Erklärung der Hawking-Strahlung), dann sorgt der Zufallscharakter der Quantenmechanik dafür, dass wir aus der Zahl aller Möglichkeiten, die sich in einem Zustand überlagern, eine bestimmte durch diese Wechselwirkung gewissermaßen “isolieren” (das genau ist ja der Messprozess). Die anderen Möglichkeiten verschwinden dann gewissermaßen, genauso wie unser Elektron, wenn wir es “hier” messen, jetzt eben mit Sicherheit nicht “da” ist.
Wenn man diese Überlegung mit einbezieht, dann ist das Bild am Ende vielleicht doch nicht ganz so schlecht.
Fazit
Tja, so kann es einem gehen: Als ich anfing, den Artikel zu schreiben, wollte ich eigentlich nur erklären, warum das übliche Bild des Vakuums schlicht falsch ist. Aber mit dem Argument der Messprozesse und der Analogie zum Kastenpotential habe ich mich jetzt doch davon überzeugt, dass es als anschauliche Umschreibung nicht so schlecht ist, wie ich vorher dachte. Die Erklärung hat den entscheidenden Nachteil, dass sie suggeriert, dass der Vakuumzustand orts- und zeitabhängig ist (und anschauliche Erklärungen, die man nicht fehlerfrei weiterdenken kann, sind ja immer ein Problem). Wenn man aber in einem populärwissenschaftichen Artikel kurz erklären will, wie es sein kann, dass im Vakuum etwas passiert und dass man da plötzlich Effekte von Teilchen im Vakuum beobachtet, gibt das Bild viele Aspekte doch richtig wieder.






Kommentare (140)