Drüben bei Alpha Cephei hat ja Alderamin gerade sehr kompetent erklärt, wie die Ausdehnung des Universums in unterschiedlichen Modellen funktioniert. Ein Aspekt dabei hat mich allerdings immer verwirrt, und den schauen wir uns heute an.
Um uns das Leben einfach zu machen, können wir heute darauf verzichten, komplizierte und unverstandene Dinge wie die dunkle Energie zu betrachten. Wir können sogar erst mal auf Materie verzichten und uns ein vollkommen leeres Universum vorstellen. Na gut, ganz leer sollte es nicht sein, denn dann können wir nichts beobachten (Raum allein ist schlecht beobachtbar). Wir bedienen uns also mal wieder meines alten Tricks’ und füllen unser Universum mit Raumzeitstaub an: Kleinen Teilchen, die wir verfolgen können, die aber so geringe Masse haben, dass sie die Raumzeit nicht krümmen.
Nehmen wir erstmal ein ganz einfaches statisches Universum. Wir haben drei Raum- und eine Zeitdimension, das macht die Sache etwas unübersichtlich, aber der Einfachheit halber können wir eine Raumdimension weglassen und uns ein zweidimensionales Universum vorstellen, wie ein gigantisches (unendliches) Blatt Papier oder eine Metallplatte.Dieses Universum ist statisch, es ändert sich mit der Zeit nicht und ist vollkommen flach. Die einzelnen Teilchen unseres Raumzeitstaubs sind alle anfangs in Ruhe und bleiben das auch, nichts bewegt sich und alles bleibt für alle Zeit gleich. Ziemlich langweilig, oder?
Machen wir es deshalb interessanter: Wir lassen unser Universum expandieren. Wir können uns zum Beispiel vorstellen, dass wir eine Metallplatte haben und diese immer weiter aufheizen. Die Metallplatte dehnt sich dann thermisch aus und all die Staubteilchen auf der Platte entfernen sich voneinander. Je weiter zwei Teilchen voneinander entfernt sind, desto größer ist ihre Geschwindigkeit relativ zueinander. Es gibt bei dieser Ausdehnung keinen Mittelpunkt, das Universum sieht von jedem Punkt aus gleich aus:
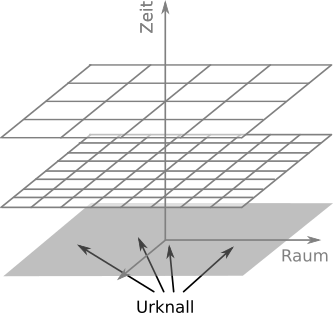
Modifiziert aus M. Bäker, “Isaac oder Die Entdeckung der Raumzeit”, Springer 2019, alle Rechte vorbehalten
Diese sich ausdehnende Metallplatte ist ein gutes Modell für ein leeres, expandierendes Universum, das sogenannte Milne-Universum. Und alle Bücher zum Thema “Expansion des Universums” sagen, dass ein solches Universum gekrümmt ist (und zwar negativ, wie die Fläche eines Sattels).
Warum soll das so sein? Wir haben doch unsere Metallplatte, und die dehnt sich an allen Punkten gleich aus. Wenn sie am Anfang flach und eben war, dann bleibt sie das doch auch, oder nicht? Wieso sollte die Platte sich plötzlich krümmen, das tut eine reale Platte ja schließlich auch nicht?
Die Antwort darauf liegt zum einen in den Effekten der speziellen Relativitätstheorie (SRT), zum anderen in der Art, wie wir eigentlich den “Raum” definieren. Laut SRT gibt es ja nicht “den Raum” und “die Zeit”, sondern es gibt eine Raumzeit, die sich für unterschiedliche Beobachterinnen unterschiedlich darstellt. Zwei Ereignisse, die für eine Beobachterin gleichzeitig sind (und deshalb nur räumlich voneinander getrennt sind), sind für eine Beobachterin, die sich mit hoher Geschwindigkeit bewegt, nicht gleichzeitig und haben einen räumlichen und einen zeitlichen Abstand.
Bei einem expandierenden Universum ändert sich der Raum ja ständig, sonst könnte er nicht expandieren. Wenn wir den Raum beschreiben wollen, müssen wir das also zu einer bestimmten Zeit tun. Und da stellt sich natürlich die Frage “Wessen Zeit?” Wie definieren wir, welche Punkte unseres Raumes (oder welche Positionen unserer Staubkörner) wir als “gleichzeitig” betrachten, damit wir die Form des Raums zu dieser Zeit bestimmen können?
Bei unserer statischen Platte war das kein Problem – erstens änderte sich nichts, zweitens bewegten sich unsere Staubkörner nicht relativ zueinander, so dass die Zeit für alle Staubkörner gleich verging. Aber wenn der Raum sich ausdehnt, dann entfernen sich die Staubkörner voneinander. Ein Staubkorn in großer Entfernung von uns hat eine hohe Geschwindigkeit und laut der SRT vergeht für dieses Staubkorn die Zeit langsamer (die berühmte Zeitdilatation).
Wir könnten das natürlich einfach in unserer Definition berücksichtigen und sagen “Gut, wir nehmen unsere Zeitvariable, und an allen anderen Punkten des Universums rechnen wir die entsprechende Zeitdilatation ein.” Dann vergeht am Ort des schnell bewegten Staubkorns real weniger Zeit als die Uhr dort anzeigt (weil für das Staubkorn ja vielleicht nur 1 Jahr vergeht, wenn es bei uns zwei Jahre sind). Das macht die Sache dann ziemlich kompliziert – bei uns sieht dann zwei Jahre nach Beginn der Expansion das Universum anders aus als bei dem anderen Staubkorn (zum Beispiel sind bei uns die Staubkörner weniger dicht gepackt, weil sie sich ja schon weiter voneinander entfernt haben). Wenn man Ereignisse im frühen Universum beschreiben will, wäre das ziemlich verwirrend.
Hinzu kommt, dass diese Definition natürlich einen Punkt im Universum auszeichnet – nämlich uns. Bei uns ist, wenn die Uhr zwei Jahre nach dem Urknall anzeigt, tatsächlich die meiste Zeit vergangen (nämlich zwei Jahre), überall sonst im Universum weniger. Auch das macht alles sehr verwirrend – die Beschreibung des Universums zu einer Zeit würde dann immer suggerieren, dass unsere Position besonders ist.
Die Zeit so zu definieren, ist also anscheinend keine gute Idee – kann man machen, macht das Leben aber unnötig kompliziert. Wenn wir in unserer Definition berücksichtigen wollen, dass das Universum überall (mehr oder weniger) identisch ist, dann sollten wir die Zeit entsprechend definieren. Das können wir natürlich tun. Wir definieren die Zeit an jedem Punkt des Universums so, dass sie gleich der Zeit ist, die für das jeweilige Staubkorn dort seit dem Urknall vergangen ist. Dann sieht das Universum zur Zeit “2 Jahre” (oder 2 Milliarden Jahre o.ä.) überall gleich aus. Erst mit dieser Definition ergeben Aussagen wie “Etwa 380000 Jahre nach dem Urknall wurde das Universum durchsichtig” Sinn – überall im Universum vergingen für eine lokale Beobachterin eben 380000 Jahre, bis das Universum durchsichtig wurde.
Aber jetzt kommt der Effekt der Zeitdilatation aus der SRT wieder ins Spiel: Aus unserer lokalen Sicht (der ersten Definition, die wir versucht haben) sind 2 Jahre nach dem Urknall vergangen, wenn für ein entferntes und schnell bewegtes Staubkorn nur ein Jahr vergangen sind. Aus unserer lokalen Sicht liegt also der Zeitpunkt, der dort “gleichzeitig” mit dem jetzigen Moment sein sollte (dort sind 2 Jahre vergangen), noch in der Zukunft. Man kann das Ganze in ein Raumzeit-Diagramm einzeichnen, das sieht dann etwa so aus:
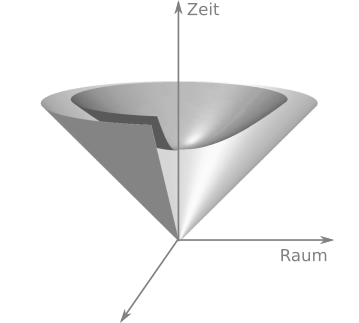
Modifiziert aus M. Bäker, “Isaac oder Die Entdeckung der Raumzeit”, Springer 2019, alle Rechte vorbehalten
Nach der neuen Definition liegen alle Ereignisse, die zur gleichen Zeit stattfinden, von unserer lokalen Warte aus gesehen “eigentlich” in der Zukunft. Das führt nicht zu Widersprüchen – in der ART haben wir bei der Definition der Raum- und Zeitkoordinaten sehr große Freiheiten, weil es für die Natur egal ist, wie wir unsere Koordinaten wählen. Aber es führt dazu, dass der Raum jetzt, bei dieser Wahl der Zeitkoordinate, gekrümmt ist, wie man im Bild ja deutlich sieht. (So etwas gibt es auch anderswo: In geeigneten Koordinaten (Gullstrand-Painleve) ist zum Beispiel der Raum um ein Schwarzes Loch herum nicht gekrümmt.)
Die Krümmung dieser Fläche ist negativ, obwohl es im Bild ja aussieht, als wäre sie eher wie eine Kugeloberfläche (also positiv gekrümmt). Das liegt daran, dass wir im Bild in der vertikalen Richtung die Zeit auftragen. Für die gilt aber in der RT eine etwas andere Geometrie als für den Raum (das habe ich hier mal kurz erklärt). Entsprechend ist ein leeres, expandierendes Universum negativ gekrümmt. (Mal wieder ein Expertinnenhinweis: In der ART spricht man nicht von einer Zeitdilatation bei den Beobachtern an unterschiedlichen Punkten – unter anderem deshalb nicht, weil man sich dort auch durchaus schneller als mit Lichtgeschwindigkeit von uns entfernen kann. Letztlich liegt das an der Definition der Zeitkoordinate: Wenn man die so definiert, wie ich es hier tue, dann ist die Zeitdilatation automatisch herausgerechnet. Alternativ kann man auch sagen, dass wir ein SRT-Modell betrachten, in dem man das mit der Krümmung leichter verstehen kann, und das übertragen wir dann auf die ART. Wer die Gleichungen dazu sehen will, findet sie im ART-Buch von Rebhan in Kap. 15.2 und 19.3.3, wo ich diese Überlegung her habe.)
Nochmal zusammengefasst: Wir nehmen ein einfaches, flaches Universum und lassen es expandieren, so wie eine Metallplatte, die sich ausdehnt. Wenn wir die Zeit in unserem Universum so definieren, dass sie gleich der lokalen Zeit ist, die eine Beobachterin an einem Ort seit dem Urknall gemessen hat, dann führt das dazu, dass Ereignisse, die nach dieser Definition “gleichzeitig” sind und die deshalb den Raum zu einem Zeitpunkt definieren, auf einer gekrümmten Fläche liegen.
Dieses Ergebnis sorgt nicht nur häufig für Verwirrung – es zeigt auch wieder einmal, wie vorsichtig man in der ART sein muss, wenn man Koordinaten definiert. Die Raumzeit ist eindeutig, aber wenn man Zeit- und Ortskoordinaten definiert, dann hängt es von deren Definition ab, wie genau der “Raum” gekrümmt ist – Raum und Zeit allein haben keine eindeutige Bedeutung.
PS: Wenn ihr mehr wissen wollt, findet ihr das alles detaillierter erklärt natürlich in meinem Buch.






Kommentare (100)