Last week I introduced a cryptogram made with a Fleissner grille. Blog reader Armin Krauß found the solution, although I had made a serious mistake in the encryption process.
First of all, I have to appologize! Last week I created a ciphertext using a Fleissner grille in order to present it as a challenge to my readers. To my regret, this cryptogram contained an error.
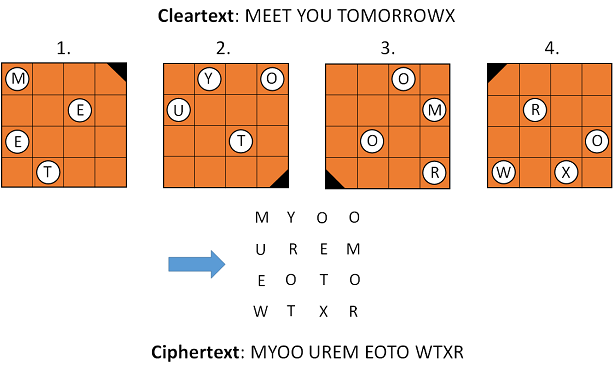
The Fleissner grille is named for Edouard Fleissner von Wostrowitz (1825–1888), who described it in one of his publications. However, this method had long been known before. Here’s how a Fleissner grille works:
The mistake I made happend in the third encryption step. I simply forgot to turn the grill (on my Powerpoint slide) before I filled in the third part of the message. I corrected this mistake immediately by turning the grille and by turning the grouped letters. Then I ungrouped the letters and turned them again. Now every letter was in a hole again, but I didn’t realise that the order of the letters was wrong now. Here’s the correct version of the challenge:
ENPAIGEZLANEDMTHSENF EIORDEMATANNATMOOFSL AEPLMHOIERITOECDMVNE OXNPBROEDOIETRANEEIU XPNPONRNTAREOMMYDWIT IANHTNEIOODNSOUOTETD MOOVEARPHRIOLAEGNALN INATTFINOREATDNGWDDA UHSIEURININGTTEDASTN ATGHPEESAOMEISEADRMM YANTSOEJOESYTERTHACH BNINCALURDCHLEALLHLA OIFWESTEHENGREERRTHE SAAMSIBEIOVNSAINARLI DTESGIIETTUCNARILYLO ESENRUUISINEADSRANLA COUWNEAUETCPOHRNSDTW BYEOFNINGHERHIVNTOTE MNTBERAEHEUNSPNSUTIX NPOITYPFIKSAVULEATRA
Interesting comments from my readers
One of the first comments to my article came from Jim Gillogly, who is known as an excellent codebreaker. One of his masterpieces was the breaking of several hundred encrypted messages sent by the Irish Republican Army (IRA) in the 1920s. The details of this story are presented in the book Decoding the IRA co-written by Jim and IRA expert Thomas Mahon. Jim also broke one of the infamous “cryptograms from the crypt” created by parapsychologist Robert Thouless in order to prove that there is a life after death.
Concerning the Fleissner challenge Jim wrote:
Although it [the codebreaking program] came up with suspiciously coherent phrases like “[he?]unitedstatesarmy” and “[posedmany?]technicalchall”, it had less coherent suggestions like “fated on..export..need someone…” and “saint carlie droe sword.figh..” and “outjest befingers meant…”.
The “suspicously coherent phrases” UNITEDSTATESARMY and POSEDMANYTECHNICALCHALL turned out to be correct, as they actually appear in the cleartext. So, Jim was the first who presented a part of the correct solution.
Martin from Switzerland, Norbert Biermann and Tony Gaffney made interesting comments, too. Only minutes before I published this article, Hendrik posted another interesting comment. Thank you to all of the contributors and sorry for not going into detail about all your ideas.
Hill Climbing
In recent years codebreakers like George Lasry, Nils Kopal, Jim Gillogly and Dan Girard have shown that Hill Climbing is a powerful technique to break old encryptions. My expectation was that Hill Climbing would work in this case, too. Hill Climbing works (in this context) like this:
- A Fleissner grille is constructed at random and used to decrypt the cipher text.
- The result is fed to a function (“cost function”) that rates the correctness of the letter sequence (for instance, based on whether the bigram frequencies ressemble the ones of English text).
- The grille is changed slightly (according to a “mutation rule”), and again the ciphertext is decrypted and rated. If the rating is better now, the current grille will be kept, otherwise the previous one is reloaded.
- Again, the grille is changed slightly, used for decryption and the result is rated, and so on.
This procedure is carried on, until the rating doesn’t improve any more. If we are lucky, this maximum rating indicates that we have found the correct grille.
Codebreaking with Hill Climbing only works if small changes in the key cause small changes in the cleartext. This is the case for many classical encryption algorithms, including the Fleissner grille. In modern cryptanalysis Hill Climbing doesn’t play any role at all, as modern encryption algorithms like AES, DES, and PRESENT are designed to be random oracles. This means that if only one bit is changed in the cleartext or the key the ciphertext changes completely. This is also referred to as “avalanche effect”.




Kommentare (5)