The straddle checkerboard was an important part of many Cold War ciphers. Can a reader decipher three ciphertexts I created with this encryption method?
Today, I’m going to address an encryption method from the Cold War: the straddle checkerboard cipher. This algorithm is a substitution cipher that replaces each letter of the alphabet with either a one-digit or a two-digit number. I will explain the straddle checkerboard cipher in the following. A more detailed description is available here.
The straddle checkerboard cipher
In order to use the straddle checkerboard cipher, we need a table with four rows. The numbers from 0 to 9 are written into the first one:
01234579 ---------- ---------- ----------
Next, we write the eight most frequent letters of the English language (ETAONISH) into the second line. The order of the letters and the position of the two empty cells are a part of the key. The two numbers above the blancs are written at the beginning of the third and fourth row (the order is key-dependent). The remaining letters are written behind the two numbers (in a key-dependet way). Again, there will be two empty cells, the positions of which are a part of the key. Here’s an example:
0123456789 HNAOTI E S 8FJUVPK WCD 6GXYBL MQRZ
Now, each letter in the second line is encrypted with the number above it. Every other letter is represented by a two-digit number consisting of the digit at the start of the line and the digit above it.
For instance, the plaintext CRYPTOLOGY encrypts to 8868628443646057.
Although some letters are replaced with a two-digit number, while others correspond to a single digit, it is possible to decrypt a ciphertext unabiguously.
The straddle checkerboard cipher can certainly be broken, unless the ciphertext is very short. However, this method is quite useful as a first step in a more complex encryption procedure. For instance, the straddle checkerboard was used as a part of the VIC cipher, a method applied by Soviet spies during the Cold War.
West German spies used the stradle checkerboard to turn a plaintext into a sequence of numbers that was encrypted with the One Time Pad. The German variants of this method had names such as DEIN STAR, STEIN RAD, or EI STRAND, as these expressions contain the eight most frequent German letters. The method DEIN STAR, for instance, required the user to write the letters DEIN_STAR_ into the line below the numbers.
Three challenges
A question I ask myself is how much ciphertext is required to break a straddle checkerboard cipher. For this reason, I created three challenges. They are based on on English plaintexts containing 30, 60, and 90 letters respectively. Here they are:
Challenge 1 (30 letters)
260355498756787990942684843799250897793
Challenge 2
429704079621964206346859079183084306033479 764248704430204998260210804343852121037642
Challenge 3
760945599283509883852848445498552445859087 493808685524807493804685381576272151878549 46754413753887609845183768721865938481544
Each message was encrypted with a different key. This means that the positions of the eight letters in the second row are different (but still, only the letters E, T, A, O, N, I, S, and H appear in this line). The positions of the remaining letters in lines three and four are different, too. The two unused digits in the first line can appear in random order at the beginning of lines three and four.
Can a reader break these messages?
Follow @KlausSchmeh
Further reading: The ciphers of spy Brian Regan
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/

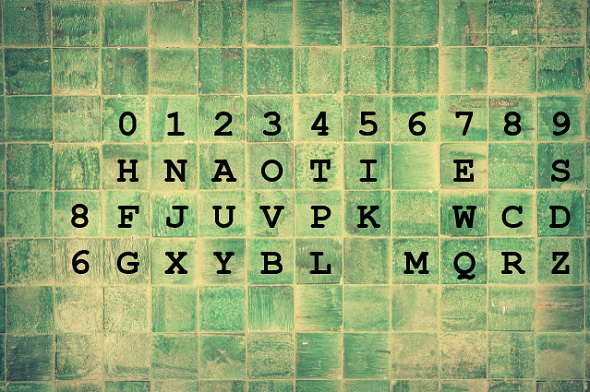

Kommentare (14)