The homophonic Polybius is a simple but hard to break manual cipher. Can a reader break a message I have encrypted in this scheme?
Designing a purely manual cipher (i.e., one that can be executed without a computer, cipher machine, or cipher tool) has proven a difficult problem. Most designs are either too complicated for practical use or insecure (some are even both). Almost all manual ciphers that were developed in the pre-computer era can today be broken with a computer program.
Although manual encryption algorithms lost importance with the advent of computer technology, they are still an active field of research.
Homophonic Polybius
Today, I’m going to present a manual cipher I call “homophonic Polybius”. It is based on the Polybius cipher, a system invented by the old Greeks, and enhanced by the use of homophones. I have never seen this system in the literature, but I can imagine that similar concepts have been used before.
The homophonic Polybius is simple, but might be hard to break. It replaces every letter of the plaintext with a letter pair (digraph), which means that the ciphertext is double as long as the plaintext. Such a property is not desirable, but can be tolerated if one is dealing with a plaintext of only a few hundred letters or less.
In the following, we work with a 25-letter alphabet. There is no Q. If a Q appears in the plaintext, we take a K instead.
For the homophonic Polybius cipher we need two keywords. As an example, we take PASTA and NOODLE. Each keyword is used to rearrange the alphabet in the following way: Write the keyword first, omit repeating letters, append the remaining letters. For PASTA we receive:
PASTBCDEFGHIJKLMNORUVWXYZ
With NOODLE, the alphabet is written as follows:
NODLEABCFGHIJKMPRSTUVWXYZ
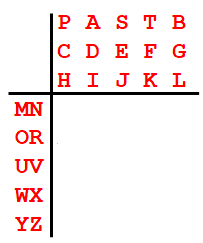
Now we construct a substitution table. In the first step, we write the PASTA alphabet as follows (three lines on the top, two columns on the left):
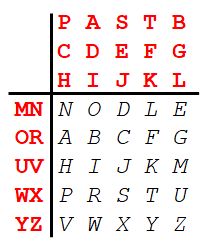
In the second step, the NOODLE alphabet is added as a five-by-five square:
With this Polybius-type substitution table, we have several options to encode each letter. For instance, the A can be encrypted as OP, OC, OH, RP, RC, or RH. In other words: We have six homophones for each letter of the alphabet. Let’s now encrypt the plaintext TO BE OR NOT TO BE:
T O B E O R N O T T O B E X XK ND OI ML ND WA MH MI WF XF MA RI NB ZJ
The ciphertext is: XK ND OI ML ND WA MH MI WF XF MA RI NB ZJ
Each letter pair in the ciphertext was randomly chosen from the six homophones available for the respective letter. For instance, the T at the beginning was encrypted as XK, but could also have been encoded as WT, WF, WK, XT, or XF. When using this scheme, one should switch between the homophones of a certain letter in a non-regular way.
A challenge
The following ciphertext has been encrypted in a homophonic Polybius cipher:
MG VI VH PG JG KE KB KB VR LU JG ZG JE VN ZD VC KA ME TB VR JS TU PG KA JS
VX VB VH PE KE VS KB PB KA MA PF ZX KA MB PA ME PI VE KI VF KB VA PD MG ZC
VB KU KS VH PE KA VC YX VE KA TS TC KA VB KI KE VB ME PR MA KH KB VC TI TU
PG KA VB VF ZF VH PE KG VN KB PC KA ME PX ZR KA MD PE MG PI VG KU VR KN VD
VR MU MG VS KG KH PF PE VU KE JA KN JN VF VH PE JA VB KN PD KG ME PR ZR KG
VI KG MG PI VD PG MG ZG KG ZB VR KN VD KU MR VU ZD VF MU VU PE KG KE KI PR
PG VU ZD VB ZF VG KG VB VD KG VN KI KE VD VG PD MG ZD KE KD VD KU KB MC KG
KB KI KN KA TI KG KA KS PG ZR KN KD VB KG KD MG KB KD MI KU LI VH KG KE KB
The plaintext is in English, consisting of 200 letters. Both keywords are misspelled expressions, which means that a dictionary attack won’t work. Can a reader solve this challenge?
Follow @KlausSchmeh
Further reading: Solve the Bigram 600 challenge and set a new world record
Linkedin: https://www.linkedin.com/groups/13501820
Facebook: https://www.facebook.com/groups/763282653806483/



Kommentare (23)