KIAS-Kalender August 2016

Japanische Tempelkunst, Zerlegungen von Polygonen und Eulers verallgemeinerte Fermat-Vermutung im neuen Kalenderblatt.

(Wie immer kann man die Bilder durch Anklicken vergrößern.)

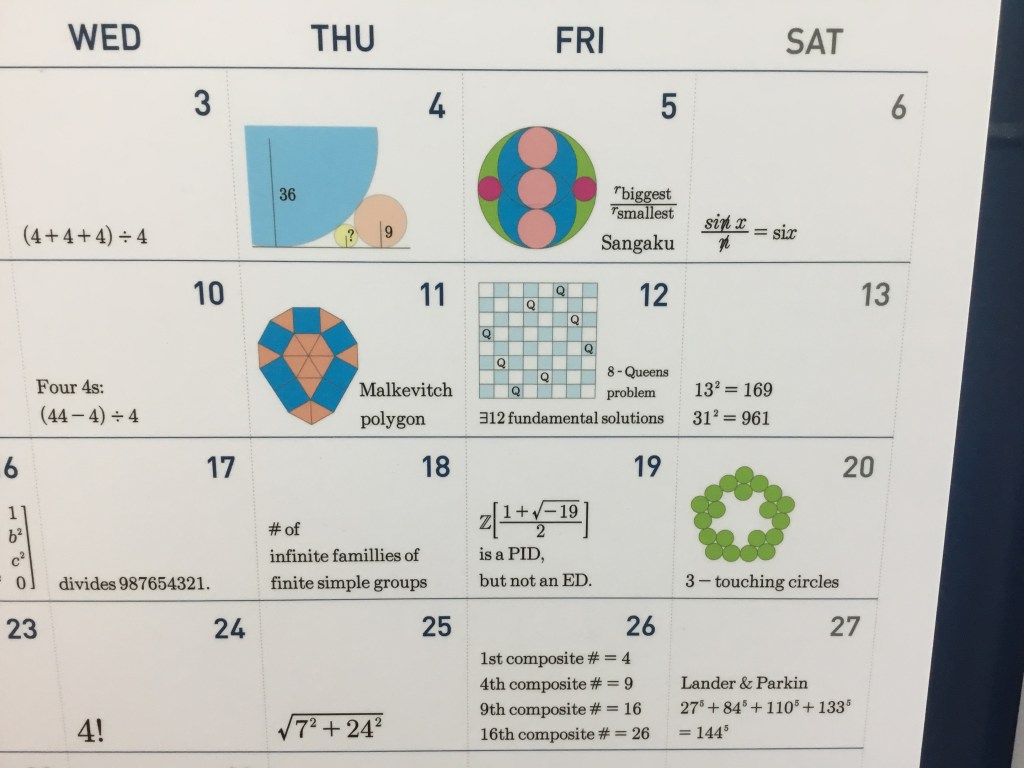
Die 2 (im Bild oben) ist natürlich einfach die Summe einer geometrischen Reihe.

Sangakus sind Holztafeln mit geometrischen Rätseln, die zwischen dem 17. und 19. Jahrhundert oft in japanischen Tempeln aufgehängt wurden. Das bei der 4 (im Bild unten) abgebildete stammt aus dem Jahr 1824. Der allgemeine Zusammenhang für die Radien der drei Kreise ist .

Bei der 5 scheint ein Fehler unterlaufen zu sein, jedenfalls ist mir nicht klar, was die blaue Fläche eigentlich sein soll. Sehr wahrscheinlich ist dieses Sangaku gemeint:

das gibt es nämlich wirklich und die Lösung ist tatsächlich .

Das Wortspiel bei der 6 soll wohl auf das trigonometrische Integral si(x) anspielen, dessen Definition aber eigentlich etwas anders geht, nämlich

Der Achterknoten bei der 8 ist das einfachste Beispiel eines hyperbolischen Knotens und sein Komplement ist das einfachste Beispiel einer hyperbolischen 3-Mannigfaltigkeit.

Jede natürliche Zahl ist die Summe von 9 dritten Potenzen: das ist ein Spezialfall des Waringschen Problems und wurde erst Anfang des 20. Jahrhunderts bewiesen.

Joseph Malkevitch beschäftigte sich in einer 1969 veröffentlichten Arbeit mit der Frage, welche Polygone in gleichseitige Drei- und Vierecke zerlegt werden können. Das Bild bei der 11 zeigt eines der exotischeren Beispiele.

Beim Damenproblem sollen acht Damen auf dem Schachbrett sich nicht schlagen können. Man weiß schon seit dem 19. Jahrhundert, dass es genau 92 Lösungen gibt, diese lassen sich auf 12 “Fundamentallösungen” zurückführen.

Bei der 14 geht es um die Anzahl unterschiedlicher Triangulierungen des Sechsecks. Wir hatten in TvF 157 mal darüber geschrieben.

Bei der 16 geht es um die Formel, mit der man den Flächeninhalt eines allgemeinen Dreiecks aus den drei Seitenlängen berechnen kann.

Bei der 18 geht es um die Klassifikation der endlichen einfachen Gruppen. Man hat die zyklischen Gruppen, die alternierenden Gruppen und 16 Serien von Gruppen vom Lie-Typ, ausserdem noch einige sporadische Gruppen.

Bei der 19 geht es um den Ring , also die Menge der komplexen Zahlen der Form mit ganzzahligen a,b. Der Ring ist kein euklidischer Ring (der euklidische Algorithmus funktioniert nicht), aber trotzdem ein Hauptidealring (man hat in diesem Ring eine eindeutige Primfaktorzerlegung).

Bei der 21 geht es um die 4-uniform tilings (3:1).

23 ist die kleinste (ungerade) Primzahl, die nicht zu einem Primzahlzwilling gehört.

Bei der 27 geht es um Eulers Verallemeinerung der Fermat-Vermutung: sie besagte, dass die Summe von weniger als k k-ten Potenzen keine k-te Potenz sein kann, also für keine ganzzahligen Lösungen habe. Das angegebene Gegenbeispiel fanden Lander und Parkin erst 1966 mit einem CDC6600.

28 Ecken hat der Coxeter-Graph, einer von nur 13 kubischen distanz-regulären Graphen.