Im letzten Artikel wurde dargelegt, wie es ein Computer schafft, Grafik im Allgemeinen auf den Bildschirm zu bringen. Speziell wurde dabei dargelegt, wie sich zweidimensionale Grafiken, sprich: Bilder, auf den Monitor zaubern lassen. Wie es aber geschafft wird, die imposanten, scheinbar dreidimensionalen Bilder in modernen Computerspielen und computergenerierten Filmen auf die Leinwand zu projizieren, soll im heutigen Artikel erklärt werden. Dazu müssen wir zwar etwas in die Welt der Mathematik abtauchen, aber zum Glück nicht allzu tief. Bevor wir aber mit der Mathematik anfangen, ein paar Worte zum Vorgehen zur Darstellung von dreidimensionalen Bildern allgemein.
Die dargestellten Bilder eines modernen Computerspiels sind natürlich nur scheinbar dreidimensional; was auf dem Monitor dargestellt wird, ist eine zweidimensionale Projektion des dreidimensionalen Bildes. Auch moderne Monitore und 3D-Brillen, die scheinbar wirklich 3D-Bilder darstellen, nutzen im Grunde lediglich flächige Bilder zur Darstellung (und haben dabei das gleiche Funktionsprinzip wie unsere Augen, die auch – jedes für sich – nur “flache Bilder” verarbeiten). Wenn im Folgenden also von 3D-Bildern die Rede ist, dann ist damit der in der Computerwelt übliche Begriff gemeint, nämlich die Darstellung eines zweidimensionalen Bildes auf der Grundlage eines dreidimensionalen Modells.
Wie kommt nun aber dieses Modell auf den Bildschirm?
Die gemeinhin verwendete Methode ist die sogenannte Rasterisation (englisch gelesen). Das darzustellende Modell wird hierbei als Szene bezeichnet; eine solche Szene besteht aus den darzustellenden
Gegenständen mit Informationen unter anderem über ihre Oberflächenstruktur und Farbgebung, aus Informationen über Lichtquellen und über diverse andere optische Effekte (Feuer, Nebel usw.). Jedes dieser sogenannten Szenenobjekte besitzt spezifische Eigenschaften, insbesondere aber natürlich eine Position und Orientierung innerhalb der Szene. Zusätzlich gibt es für jede Szene (mindestens) eine Kamera, die gewissermaßen den Standpunkt und die Orientierung des Beobachters beschreibt, mithin also definiert, was für ein Bild angezeigt werden soll. Die Szene ist dabei in ein
dreidimensionales Koordinatensystem, das sogenannte Weltkoordinatensystem, eingebettet; das könnte etwa so aussehen:

Nun bleibt natürlich immer noch die Frage, wie die so beschriebene Szene mit Hilfe der Kamera-Information auf den Bildschirm gezeichnet werden kann. Es entsteht sogar ein zusätzliches Problem: die Szenen-Informationen liegen im 3D-Raum; so bestehen zum Beispiel Positionsangaben aus drei Werten, nämlich der Position in Breite, Höhe und Tiefe (im Allgemeinen als X-, Y- und Z-Position
bezeichnet). Auf einem Bildschirm können aber nur Positionen mit zwei Werten – der Breite und der Höhe – gezeichnet werden. Es gilt nun also nicht nur zu berechnen, welche Objekte überhaupt gezeichnet werden müssen, sondern es müssen auch die dreidimensionalen Positionsangaben der Szene in die zweidimensionalen Angaben das Backbuffers (wir erinnern uns) umgerechnet werden.
Das Zauberwort, um nun diese Magie zu bewerkstelligen, heißt Projektion. Die Idee dahinter ist relativ einfach (zur zugrundeliegenden Mathematik kommen wir gleich): es werden alle in der Szene enthaltenen Punkte (was genau ein Punkt ist, sehen wir auch gleich noch) bzw. genauer, die dreidimensionalen Positionen der Punkte – ihre Koordinaten -, hergenommen und mit einer mathematischen Struktur, die aus den Kamerainformationen aufgebaut wird, verrechnet. Diese Verrechnung führt dazu, dass die ehemalige dreidimensionale Position auf eine zweidimensionale umgerechnet wird; der Clou bei der Sache ist, dass die Koordinaten der Punkte dabei so umgerechnet werden, dass die berechneten Zahlenwerte direkt den Positionen im Backbuffer entsprechen, an welche die Punkte gezeichnet werden sollen.
Die mathematischen Strukturen, die für diese Art der Zahlenmagie benötigt werden, dürften jedem aus dem Mathematikunterricht bekannt sein: Vektoren und Matrizen.
Zur Erinnerung: ein Vektor ist ein n-Tupel gleichartiger Elemente, in der Regel auf dem Raum der reellen Zahlen, formal notiert für den Vektor v also: v ∈ ℝn. Konkrete Vektoren werden mit Hilfe einer großen Klammer geschrieben, etwa so (einmal ein ganz allgemeiner Vektor mit 3 bezeichneten Positionen und einmal ein ganz konkreter Vektor):
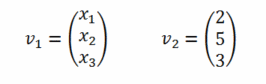 Die Rechenregeln für Vektoren sind relativ einfach: die Addition zweier Vektoren erfolgt durch elementweises addieren der einzelnen Vektor-Positionen; die Multiplikation mit einem Skalar erfolgt, indem jedes Element des Vektors mit dem Skalar multipliziert wird. Zusätzlich gibt es noch das sogenannte Skalarprodukt zweier Vektoren, bei dem die Elemente beider Vektoren paarweise multipliziert und die Ergebnisse aufaddiert werden (das Ergebnis ist also eine Zahl, kein Vektor), sowie das Kreuzprodukt mit einer etwas komplexeren Berechnungsregel, wobei das Ergebnis des Kreuzprodukts zweier Vektoren immer ein Vektor ist, der senkrecht auf beiden steht (eine in der Computergrafik sehr oft benötigte Rechenoperation).
Die Rechenregeln für Vektoren sind relativ einfach: die Addition zweier Vektoren erfolgt durch elementweises addieren der einzelnen Vektor-Positionen; die Multiplikation mit einem Skalar erfolgt, indem jedes Element des Vektors mit dem Skalar multipliziert wird. Zusätzlich gibt es noch das sogenannte Skalarprodukt zweier Vektoren, bei dem die Elemente beider Vektoren paarweise multipliziert und die Ergebnisse aufaddiert werden (das Ergebnis ist also eine Zahl, kein Vektor), sowie das Kreuzprodukt mit einer etwas komplexeren Berechnungsregel, wobei das Ergebnis des Kreuzprodukts zweier Vektoren immer ein Vektor ist, der senkrecht auf beiden steht (eine in der Computergrafik sehr oft benötigte Rechenoperation).
Eine Matrix ist – grob gesagt – ein Vektor mit (potentiell) mehr als einer Spalte; konsequenterweise werden sie auch ähnlich notiert, in etwa so:
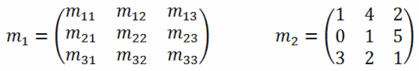
Auch für Matrizen gibt es natürlich Rechenregeln; die für die Computergrafik relevanten sind vor allem die Multiplikation zweier Matrizen sowie die Multiplikation einer Matrix mit einem Vektor (der ja im Grunde nur eine Matrix mit einer Spalte ist). Zwei Matrizen können miteinander multipliziert werden, wenn die erste Matrix genauso viele Spalten wie die zweite Zeilen hat; formal ausgedrückt: eine l×m-Matrix kann mit einer m×n-Matrix verrechnet werden, wobei das Ergebnis eine l×n-Matrix ist. Dies geschieht, indem die Ergebnismatrix nach folgender Formel aufgebaut wird (multipliziert werden hier die Matrizen a und b):
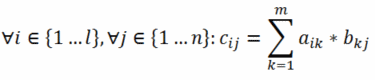
Die Multiplikation einer m×m-Matrix mit einer m×1-Matrix (einer Matrix mit einer Spalte – also ein Vektor) ist demzufolge wieder eine m×1-Matrix, also ein Vektor. Matrizen können in der Computergrafik dazu benutzt werden, um sogenannte Transformationen mit Hilfe von Transformationsmatrizen zu beschreiben. Eine Transformation bezeichnet dabei die Verschiebung eines Punktes nach einem gewünschten Schema und wird erreicht, indem der Vektor des zu transformierenden Punktes mit der passenden Transformationsmatrix multipliziert wird. Die Multiplikation zweier Transformationsmatrizen führt dagegen zu einer Matrix, welche die aufeinanderfolgende Durchführung der beiden Einzeltransformationen beschreibt.
Diese Mittel reichen bereits, um die beschriebene Projektion von Punkten durchzuführen. Die darzustellenden Punkte der Szene werden dabei zunächst einfach über Vektoren beschrieben; da wir dreidimensionale Punkte betrachten, haben die Vektoren auch entsprechend drei Werte. Zur Durchführung werden nun noch zwei Matrizen benötigt.
Die erste ist die sogenannte View Matrix, welche einen Punktes aus dem Weltkoordinatensystem (sprich: dem Koordinatensystem der Szene) in das Kamerakoordinatensystem (also in ein Koordinatensystem aus Sicht der Kamera) überführt. Praktisch kann man sich das folgendermaßen vorstellen: im Weltkoordinatensystem liegen die einzelnen Punkte beliebig im Raum verteilt; auch die Kamera ist in diesem System an einer beliebigen Stelle zu finden. Im Kamerakoordinatensystem bildet die Position der Kamera dagegen den Ursprung des Koordinatensystems, welches zudem noch entsprechend der Kameraausrichtung rotiert ist (so dass z.B. die Z-Achse im Kamerakoordinatensystem immer in Blickrichtung der Kamera, die X-Achse nach rechts und die Y-Achse nach oben zeigt). Bildlich dargestellt könnte eine derartige View Transformation also so aussehen (mit Objekten anstelle von Punkten zur besseren Verdeutlichung):
Die zweite benötigte Matrix zur Durchführung der Projektion ist die Projection Matrix (deutsch Projektionsmatrix); sie projiziert einen dreidimensionalen Punkt auf eine zweidimensionale Fläche. In der Computergrafik heißt das, dass die dreidimensionalen Punkte im Kamerakoordinatensystem (also aus Sicht der Kamera) auf zweidimensionale Koordinaten abgebildet werden, die ihrer Position auf dem Bildschirm entsprechen. Die Projektion kann dabei auf unterschiedliche Arten erfolgen, insbesondere kann eine Parallelprojektion oder eine perspektivische Projektion durchgeführt werden (für Details bitte hier schauen).
Das Ergebnis der Verrechnung eines Punktes im Kamerakoordinatensystem mit der Projection Matrix kann also direkt in den Backbuffer gezeichnet werden; fast zumindest. Aufmerksame Leser werden sicherlich bemerkt haben, dass das Ergebnis der Multiplikation einer 3×3-Matrix mit einer 3×1-Matrix (einem Vektor) ja wieder eine 3×1-Matrix, also ein Vektor mit 3 Elementen, ist – benötigt werden aber nur 2 Werte (nämlich die x- und y-Position auf der zweidimensionalen Fläche). Die ersten beiden Werte im Ergebnisvektor entsprechen nach der Projektion auch tatsächlich den
gesuchten Positionen; der dritte Wert dagegen gibt die sogenannte Tiefe des Punktes auf der zweidimensionalen Fläche an, kann also benutzt werden, um zu bestimmen, wie weit ein Punkt relativ zu anderen Punkten von der Kamera entfernt war – das ist zum Beispiel für Überdeckungstests wichtig, aber dazu vielleicht in einem späteren Artikel mehr.
Zur Erstellung der View- und Projection-Matrizen gibt es mathematische Methoden, die genau das bewerkstelligen (mit denen ich meine Leser hier aber nicht langweilen möchte). Es reicht zu wissen, dass aus den Angaben über Kameraposition und -orientierung im Weltkoordinatensystem eine View- und aus den Angaben über die gewünschte Projektion (also z.B., ob es eine Parallelprojektion oder eine perspektivische Projektion sein soll) eine Projection-Matrix berechnet werden kann. Mit diesen beiden Matrizen können nun die einzelnen Punkte der Szene in Bildschirmkoordinaten umgerechnet und in den Backbuffer gezeichnet werden – fertig ist die Projektion eines dreidimensionalen Bildes auf eine zweidimensionale Fläche.
Gut, so einfach ist es am Ende dann doch nicht; ich habe bisher lediglich von Punkten gesprochen. Aus Punkten allein kann man aber nur schlecht eine komplexe Szene aufbauen, da man ziemlich viele Punkte benötigen würde, um einigermaßen komplexe Dinge darstellen zu können (teilweise gibt es das auch in der Computergrafik; das wird dann Voxelgrafik genannt, ist aber ziemlich speicher- und rechenaufwendig). In modernen Computerspielen kommen daher sogenannte Polygonnetze (auf englisch Polygon Meshes oder meist kurz Meshes) zum Einsatz – darüber aber dann das nächste mal mehr.

Kommentare (13)