Diesen Monat durfte ich in Bremen eine Vorlesung in Thermodynamik übernehmen und bin während der Vorbereitung über ein sehr interessantes Paper gestoßen. Das Problem bei diesem Artikel wird leider, dass ich auf viele Details nicht eingehen kann, um den Rahmen nicht zu sprengen. Ich bin daher gespannt, ob der Artikel mehr Verwirrung stiftet, als Wissen vermittelt…
Thema meiner Vorlesung war der Carnot-Kreisprozess. Dieser Kreisprozess (hier geht es mit der Verwirrung schon los…) ist ein um 1820 entstandenes Gedankenexperiment des französischen Wissenschaftlers Nicolas Carnot der als der Begründer der Thermodynamik gilt. Ganz knapp beschrieben, überlegte sich Carnot einen Kreisprozess der aus vier einzelnen Schritten besteht. Als Beispiel könnte man sich Energieerzeugung in einem Kraftwerk oder einem Automotor vorstellen. Zwei dieser vier Schritte sind dabei adiabat und zwei isotherm. Adiabat heißt, dass keine Wärme zu- oder abgeführt wird und isotherm, dass sich die Wärme während des Prozessschrittes nicht ändert, also Wärme zu- oder abgeführt wird. Um das ganze wirklich verstehen zu können, müsste man noch etwas mehr ins Detail gehen (was ich auch gerne bei Bedarf mal machen werde😊), aber wichtig ist, dass Carnot mit seinem Gedankenexperiment die Energieerzeugung in einem Kraftwerk oder Auto anhand dieser vier Schritte sehr gut abbilden konnte.
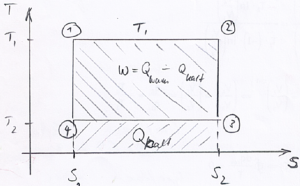
Der Carnot-Kreisprozess in einem Temperatur-Entropie Diagramm. Die Zahlen zeigen die Startpunkte der Schritte 1 bis 4. Das geschlossene Viereck ist die Erklärung warum es ein Kreisprozess ist.
Das Ergebnis seiner Überlegungen ist der theoretisch maximal mögliche Wirkungsgrad eines Kraftwerkes oder Automotors. Dieser gibt an wieviel Prozent der hineingesteckten Energie in eine andere Energieform umgewandelt werden kann und hängt stark von den Temperaturen in den Prozessen ab. Allgemein kann man sagen, je wärmer der Prozess, umso besser der Wirkungsgrad. Das der Carnot-Prozess das theoretische Limit abbildet über das wir nicht hinauskönnen, lernt jeder Student in der Thermodynamik Vorlesung.
Das Paper, das ich zur Vorbereitung gefunden haben, hebt aber genau dieses Limit auf! In dem Artikel Brownian Carnot engine vom Oktober 2015 beschreiben die Autoren wie sie den Carnot-Kreisprozess, anstatt an einem makroskopischen Kraftwerk, an einem einzelnen mikroskopischen Polystyrenpartikel durchgeführt haben. Dafür mussten sie jeden der vier Prozessschritte an dem Partikel simulieren. Die Umsetzung dieses Experiments hört sich einfach an, ist aber hochkomplex. Der klassische Carnot-Kreisprozess wird in einem Temperatur-Entropie Diagramm dargestellt (Tja die Frage was Entropie ist würde auch wieder ‘nen eigenen Artikel füllen, Temperatur ist hoffentlich den Meisten bekannt…). Die entschiedene Frage für das Experiment war, wie man ein solches Diagramm messen kann. Dafür wurden die Polysterenpartikel in einem Wasserbad versenkt. Temperatur kann man leicht messen, aber für die Entropie musste man sich eines Tricks bedienen. Dafür hat man das Partikel optisch gefangen (wassss??). Man kann sich diese optische Bodenfalle wie eine Falle aus einem Bugs Bunny Zeichentrickfilm vorstellen, je steiler die Wände umso schwieriger kommt derjenige heraus der reingefallen ist. Genau solch einen Parameter hat man in Form der Steifigkeit der optischen Falle, man kann es dem Partikel also leichter oder schwieriger machen dort herauszukommen. Damit hatte man dann die beiden nötigen Paramater (Temperatur – Steifigkeit) um den Carnot-Kreisprozess simulieren zu können.
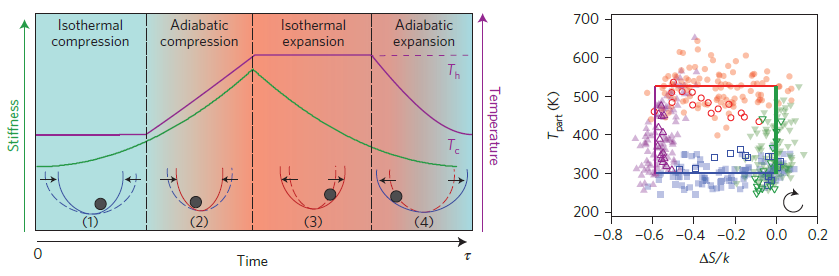
Die Bilder zeigen schematisch die vier Prozessschritte und die Änderung der beiden Parameter Steifigkeit und Temperatur, sowie dass daraus resultierende Temperatur-Entropie Diagramm, dass dem Oben sehr ähnelt… Reprinted with permission of © 2016 Macmillan Publishers Limited. All rights reserved.
Die entscheidende Neuheit ist die wieder einmal die Größe. Während Kraftwerksprozesse als Kontinuumsprozesse beschrieben werden, werden mikroskopische Prozesse stochastisch beschrieben (???). Das führt dazu, dass mikroskopische Prozesse Fluktuationen unterliegen. Zum Beispiel kann die Temperatur örtlich fluktuieren, was bei makroskopischen Prozessen in der Regel ignoriert wird. Genau diese Fluktuation führen dazu, dass der am Polysterenpartikel gemessene Wirkungsgrad manchmal höher ist, als von Carnot vorhergesagt.
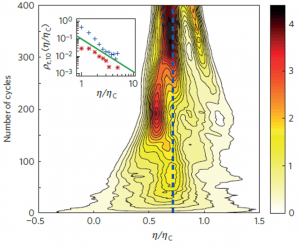
Das Diagramm zeigt die Verteilung der gemessen Wirkungsgradwerte bezogen auf den Carnot-Wirkungsgrad. Man sieht das gerade bei späteren Versuchen (n > 200) Der Wert oft über 1 liegt und damit höher als Der Carnot-Wirkungsgrad ist. Reprinted with permission of © 2016 Macmillan Publishers Limited. All rights reserved.
Was sich jetzt wahrscheinlich nicht so spannend anhört ist eine kleine Sensation, da das Carnotlimit neu interpretiert werden muss. Diese Ergebnisse sind nicht nur theoretisch sehr cool, sondern haben auch direkt einen Einfluss auf den Wirkungsgrad von molekularen Biomotoren und Mikromaschinen und werden daher bei deren Entwicklung und Design sehr sehr wichtig.



Kommentare (5)