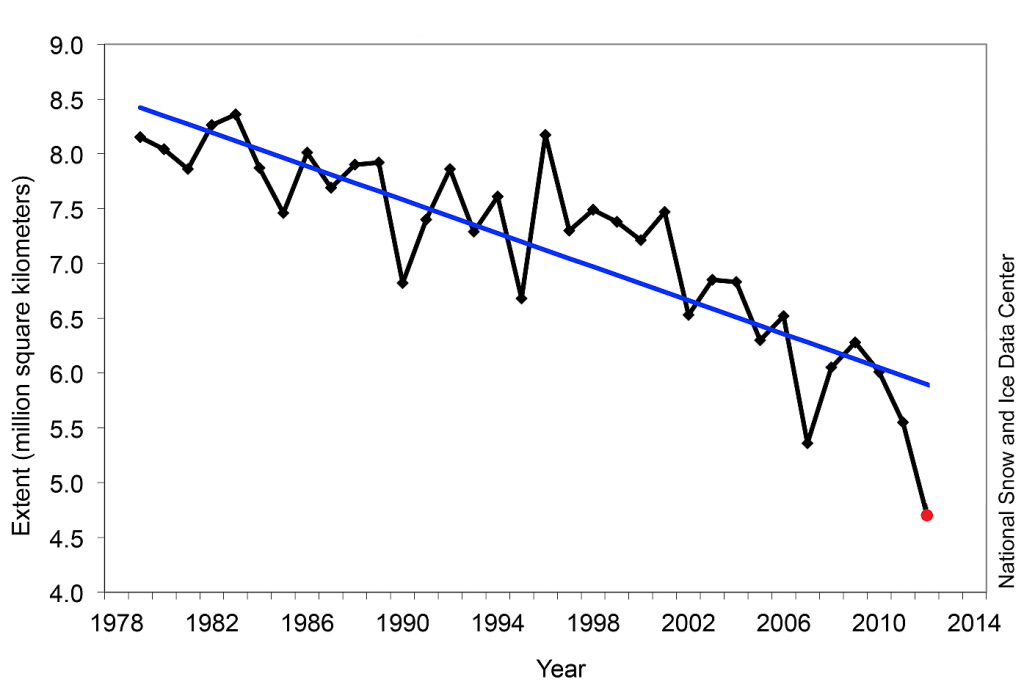
Oha! Ein gewaltiger Ausreißer nach unten, ein neuer Tiefstwert. An sich ist die Entwicklung der Eisbedeckung äußerst dramatisch, aber ein einzelner Datenpunkt, erst recht ein Outlier, sagt nur wenig aus. Wie mag die Eisbedeckung weiter verlaufen sein?
Müssen wir eine zweite Regressionsgerade einzeichnen, viel tiefer als die erste – macht der Verlauf der Eisbedeckung also einen Sprung? Oder ist vielleicht eine andere Regressionskurve höheren Grades (also eine gebogene) besser geeignet? Werden die Jayhawks nach 11 gewonnenen Spielen auch in der darauffolgenden Season 11 Spiele am Stück gewinnen?
2013:
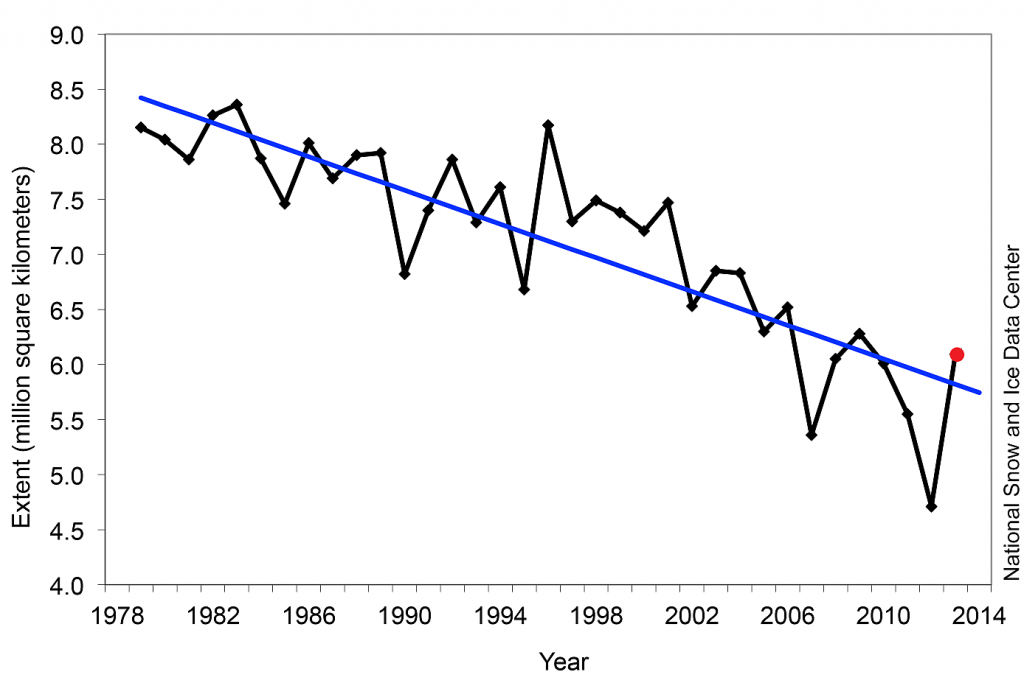
Wer bis hierhin gelesen hat, wird davon wenig überrascht sein. Auf einen Outlier folgt mit einer großen Wahrscheinlichkeit eine Rückkehr zum Mittelmaß, eine Regression zur Mitte – wobei die Mitte hier eine abfallende Gerade ist. Es kam genau das heraus, was die meisten erwartet haben, der “Eiszuwachs” (mit ganz dicken Anführungszeichen) von 2012 auf 2013 ist keine Überraschung.
Aber es gibt noch ein weiteres Problem, eine Wahrnehmungsfalle – je dichter sich die Eisbedeckung dem Nullpunkt nähert, desto größer werden die prozentualen Unterschiede zwischen den einzelnen Minima. Man könnte den Unterschied zwischen 2012 und 2013 so auslegen, als sei das Eis drastisch angewachsen – wenn man die absoluten Minimalwerte nimmt, kommt man sogar auf 60%. Für viele ein gefundenes Fressen, um Leser oder Zuhörer mit großen Prozentzahlen zu beeindrucken.
Letztes Jahr nutzte der Vorsitzende der UK Independence Party, Nigel Farage, in einer Rede im europäischen Parlament den “Anstieg” als ein Hauptargument, warum Klimaschutz völliger Käse sei und hatte sich dafür sogar zwei Satellitenfotos ausgedruckt. Die UKIP holte in der darauffolgenden EU-Wahl übrigens die meisten Stimmen in Großbritannien. (Timestamp bei Minute 2:20)
60% Anstieg innerhalb eines Jahres! Potzblitz! Das sind ja in 10 Jahren eine Versechsfachung der Eisfläche! Alles Klimaschwindel!
Die Bild-Zeitung schrieb vor wenigen Tagen: Und die Polschmelze? Vergangenen Sommer wuchs die Eisfläche in der Arktis im Vorjahresvergleich um 60 Prozent. 20 Schiffe mussten von Eisbrechern befreit werden. (Link)
Dass der “Anstieg” um 60% wegen der Regression zur Mitte zu erwarten war und der Absolutwert damit immer noch einer der niedrigsten überhaupt ist, möchte die Bild ihren Lesern hingegen nicht mitteilen. Enttäuschend, da ich die Bild bisher in der Berichterstattung über den Klimawandel eigentlich ganz gut fand.
Ins gleiche Klo greifen auch die BZ Berlin (die dem Zuwachs einen ganzen Artikel widmete), die Daily Mail (“And now it’s global COOLING! Return of Arctic ice cap as it grows by 29% in a year”) und Fox News (“Arctic Sea Ice up 60 percent in 2013”). Vermutlich gab es noch viel mehr, das sind nur ein paar, die ich auf die Schnelle ergoogelt habe. Die genauen Prozentzahlen weichen ein bisschen voneinander ab, je nachdem mit welcher Definition von Meereis man arbeitet und ob man die Minimalbedeckung oder die Durchschnittsbedeckung nimmt.
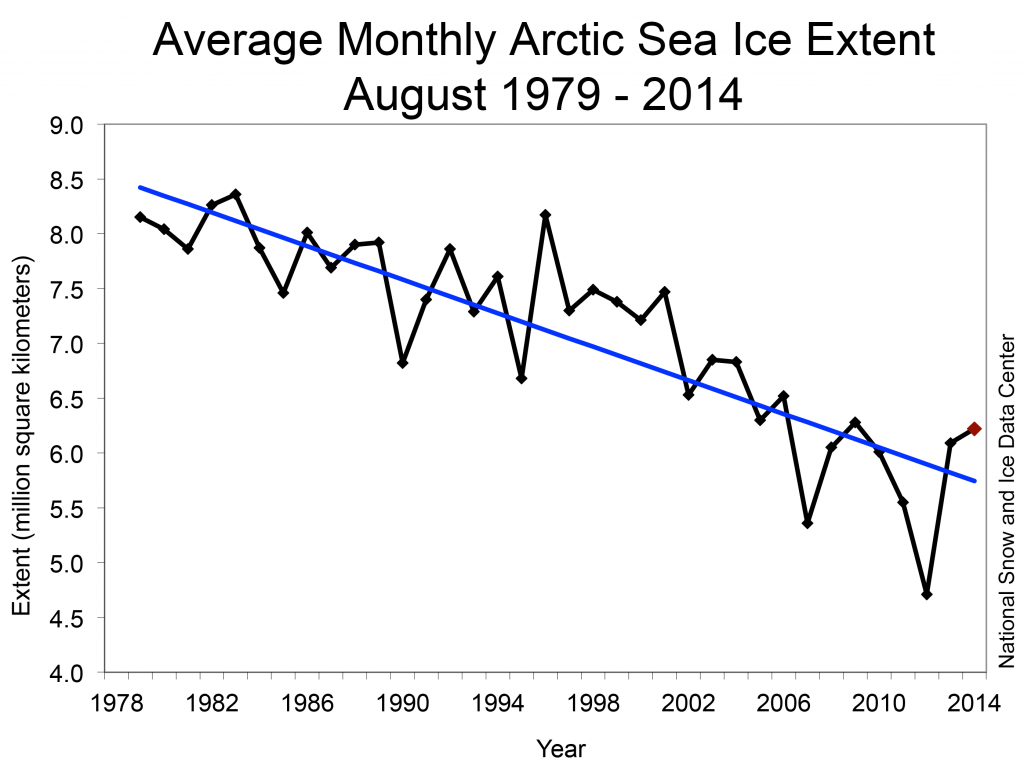
Für den September 2014 gibt es übrigens noch keine Daten, aber für den August, was dann auch unsere Grafik von oben vervollständigt:
Wie manche das wohl drehen werden? Ich glaube diesmal nicht, dass jemand daraus eine Schlagzeile machen wird. Schließlich wird der prozentuale Zuwachs von 2013 auf 2014 nur minimal sein. Dass man aus der Entwicklung der Eisbedeckung von einem Jahr zum nächsten genauso wenig eine Aussage treffen kann, wie aus zwei am Strand auslaufenden Wellen das Eintreffen von Ebbe oder Flut bestimmen zu wollen, sei dahin gestellt.
Der Zeitpunkt des völligen Abschmelzens lässt sich nur sehr grob abschätzen, nach meinem Eindruck gehen die meisten Klimawissenschaftler von etwa 10-50 Jahren aus – auf jeden Fall viel schneller, als noch zu Beginn der Satellitenmessungen vermutet wurde. Wenn wir die obige Grafik als Richtwert nehmen, erkennen wir ein Abfallen von etwa 0,75 Mio. km² pro Jahrzehnt mit einer Schwankungsbreite von etwa 1,5 Mio. km² von Jahr zu Jahr.
Kommentare (13)