Die Gravitation. Jeder kennt sie, jeder merkt sie, aber kaum einer weiß eigentlich, was sie ist oder kann gar in ihr lesen. In Teil eins erfahren wir, warum die Erde mit uns Kirmes spielt und die Olympischen Spiele in Mexiko City eigentlich “unfair” waren.
Dafür muss ich etwas ausholen und *Rotalarm, Rotalarm, Rotalarm* werde das erste Mal Mathematik und Formeln verwenden.
Also eigentlich ist alles ganz einfach
Aus dem Newtonsche Gravitationsgesetz kriegt man eine ganz einfache Formel für das Schwerefeld eines Körpers heraus:

Bild: Ein Round-Up. Eine Teufelsmaschine, in der Menschen sich für Geld nach außen schleudern lassen, wo zum Glück eine Wand ist, die ein weiteres Entweichen verhindert. Völlig meschugge. Mein Mann liebt diese Dinger. Und das macht die Erde die ganze Zeit mit uns allen – und wir merken es noch nicht mal!
Einige Orte der Erde werden stärker rumgeschleudert als andere und genau zwei Orte auf der Erde überhaupt nicht: der geographische Nord- und Südpol nämlich. Dort merken wir von der Zentrifugalkraft der Erde gar nichts, dafür aber die Erdanziehungkraft. Am Äquator dagegen ist selbst auf einer perfekten Kugel der Abstand zur Drehachse der Erde maximal und die Zentrifugalkraft wirkt der Erdanziehungskraft entgegen. Die Schwerebeschleunigung, die wir merken, ist also in Wirklichkeit die Beschleunigung aufgrund der Gravitation abzüglich der Zentrifugalbeschleunigung, weil die Erde sich um sich selbst dreht.
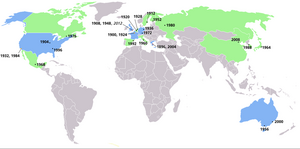
Bild: Olympische Sommerspiele Austragungsorte. Mexiko-City hatte rein von der Schwerebeschleunigung her “unfaire” Vorteile.
Es ist sogar noch schlimmer.
Ist die Erde mehr Bert oder mehr Ernie?
Habt Ihr gelernt, dass die Erde eine Kugel ist? Ist Euer Globus aus dem Kaufhaus rund?
Ihr müsst jetzt ganz, ganz stark sein: Alles gelogen 😉
Bild: Ernie und Bert aus der Sesamstraße. Als ich klein war, galt das als kindergerechtes Qualitätsfernsehen. Hey, ich hab schon lange nicht mehr Sesamstraße gesehen. Läuft das eigentlich noch?
Da die Erde sich dreht und das Gestein unter unseren Füßen nicht so fest ist, wie wir uns das immer so vorstellen, ist die Antwort: Die Erde ähnelt in ihrer Form eher dem Kopf von Ernie. Die Erde selbst gibt der Zentrifugalkraft nach, so dass sie sich am Äquator etwas ausbeult.
Die Erde ist am Äquator etwa 23 km dicker als an den Polen. Dadurch ist man am Äquator aber noch weiter weg von der Rotationsachse, als wenn die Erde eine perfekte Kugel wäre. Die Schwerebeschleunigung wird dadurch am Äquator noch ein bisschen mehr herabgesetzt. Der Vorteil für die Sportler in Mexiko-Stadt noch ausgeprägter.
Tatsächlich purzelten 1968 jede Menge Leichtathletik-Rekode und der Weitsprungrekord wurde erst 23 Jahre später überboten.
Ok, der Unterschied zwischen Schwerkraft am Pol und Äquator beträgt etwa 0,53 Prozent und 23 km mehr oder weniger macht aus einer Kugel mit volumetrischen Erdradius von 6371 km auch keinen Medizinball, aber all diese kleinen feinen Unterschiede kann der ESA-Satellit GOCE messen, der am 17. März erfolgreich gestartet ist, – und noch viel mehr.
Bild: Verschiedene Abplattungen einer Kugel. Die Abplattung der Erde beträgt etwa weniger als 1/300.

Kommentare (40)