Warum fließt Wasser manchmal bergauf und was hat das damit zu tun, dass Stockholm trocken fällt?
Im ersten Teil habe ich versucht zu erklären, dass eigentlich alles ganz einfach ist, wenn man es aus der Ferne betrachtet. Und dass die Schwerebeschleunigung g das ist, was man eigentlich auf der Erde misst.
Heute werde ich (versuchen zu) erklären, dass es beliebig kompliziert wird, wenn man es ganz ganz genau betrachtet. Denn tatsächlich ist das Schwerefeld der Erde aus dem ersten Teil eine Näherung. Eine sehr gute Näherung, die für viele Anwendungen wohl ausreichen wird, aber immer noch eine Näherung, die verbesserungsfähig ist.
Denn letztendlich stimmen verschiedene Annahmen nicht, die ich in Teil 1 stillschweigend vorausgesetzt habe:
1. Der Körper ist perfekt kugelförmig. Wobei diese Regel bereits dadurch verletzt wird, dass die Erde sich um sich selbst dreht und deswegen ein wenig am Äquator ausbeult.
2. Die Masse verteilt sich überall im Erdball gleichmäßig. D.h. die Dichte ist überall gleich.
3. Es ändert sich nichts, wenn man nach einer Stunde/ einem halben Tag/halbem Jahr oder Jahrhundert wieder hinschaut.
Die Wirklichkeit sieht natürlich etwas anders aus und jede Abweichung bzw. Unperfektheit sorgt für “Dellen” und “Beulen” in dem Gravitationsfeld. Umgekehrt betrachtet: Wenn man “Dellen” und “Beulen” misst, erfährt man dadurch Dinge von Mutter Erde, die man bis dahin gar nicht wusste. Das ist bei uns Menschen gar nicht so anders. Dellen im Bauchbereich einer Frau, die im Verlauf von neun Monaten immer ausgeprägt werden, erzählen ja auch eine ganz deutliche Sprache: Einen Vorrat an Windeln und Babynahrung anlegen! (Alternativ, wenn der Bauch nach 10 Monaten immer noch da ist, sollte man das Thema plötzliche Gewichtszunahme taktvoll vermeiden.)
Wie beschreibt man nun mathematisch ein ausgebeultes Feld?
Man nehme ein großes scharfes Messer und teile den Erdball in viele kleine Stücke bzw. Bereiche auf. Da die Erde und das Feld doch annähernd kreisförmig ist, bietet sich natürlich die Unterteilung in Kreissegmente an. Das sieht dann mathematisch so aus:
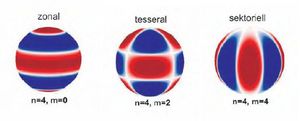
So sieht die Unterteilung für bestimmte Werte von m und n aus.
Diese einzelnen Abschnitte kann man nun abzählen und sagen: Der Bereich 8,4 hat eine Ausbuchtung von etwa 1 Promille über dem Mittelwert. Oder aber der Bereich 8,8 hat eine Delle von einem Promille unter dem Mittelwert. In diesen Bereichen der Erde würde die Waage bei gleicher Menge auf einmal mehr bzw. weniger anzeigen.
Und diese Aussagen steckt man in das dazugehörige Cnm und Snm. Das sind nämlich die Terme, die anzeigen wie weit an dieser Stelle das Feld von dem perfekten kugelsymmetrischen Fall abweicht. Bzw. diese zeigen an, wie sich die Massen in und auf der Erdkugel jetzt genau in den einzelnen Bereichen der Erdkugel verteilen. In diesen Werten steckt alles drin, was man als Geophysiker wissen will.
Wenn wir z.B. n = 1 wählen, machen wir auch nur einen Schnitt durch die Erde. Horizontal bzw. vertikal. Die Erdkugel teilen wir also in zwei Hälften. Das können wir einmal entlang des Äquators machen und kriegen so den Unterschied zwischen Nord- und Südhalbkugel und einmal z.B. entlang des Nullmeridians und kriegen so den Unterschied zwischen Ost- und Westhemisphäre. Da Nord- und Süd und Ost und Westhalbkugel gleich schwer sind, sind diese Teile = 0. D.h. diesen Term können wir bei der Erde getrost vernachlässigen.
Spannend wird es über den dritten Teil der Summe, wenn wir n =2 wählen, d.h. zweimal durch die Erde schneiden. Denn damit können wir ins Innere der Erde schauen. Hier stecken Teile des so genannten Trägheitsmomentes drin. Grob gesagt sagt uns das, wie schwierig es ist, die Erde um eine bestimmte Achse zu drehen oder wie sich die Massen in Bezug zu dieser Drehachse verteilen.
Genauer gesagt wird dieser Teil:

Bild: Normierte Trägheitsmomente für verschiedene Massenverteilungen. (Den Vortrag dazu gibt es hier.)
Für die Erde beträgt der Wert 0,331. Da dies kleiner als 0,4 ist, sagt und das, dass die Erde einen schweren Kern in der Mitte hat, während weiter außen die leichteren Elemente liegen.
So und wenn man die Aufteilung noch feiner macht, dann kann man genau bestimmen, wie das Schwerepotential in jedem Bereich der Erde aussieht. Bestünde die Oberfläche der Erde komplett aus Wasser, dann würde sich die Wasseroberfläche exakt daran orientieren und eine Äquipotentialfläche bilden. Für die Ozeane stimmt das auch. Das führt manchmal dazu, dass Wasser zu einem Ort fließt, der geographisch höher liegt. Weil es dort eine Delle im Gravitationsfeld gibt, die für uns Menschen erstmal unsichtbar ist, wenn wir nicht die Schwerebeschleunigung messen. Das ist z.B. im indischen Ozean der Fall, wie man anhand des gemessenen Geoiden feststellen kann:
Bild: Der Geoid hoffnungslos übertrieben. Deutlich sichtbar ist die Delle vor Indien, die letztendlich ein deutliches Zeichen für plattentektonische Aktivität in diesem Bereich ist bzw. hier wird der Ozeanboden gestreckt, weil sich Indien und die Antarktis immer weiter voneinander entfernen. Solche Schwerefeldmessungen belegen also eindeutig, dass die Erdplatten sich wirklich gegeneinander verschieben.
Hier gibt es eine Animation des Geoiden von unseren Kollegen aus Potsdam: Geoid-Animation.
Der Geoid ist übrigens kein reines Instrument für Wissenschaftler. Bereits Schulatlanten brauchen den als Grundlage von Landkarten. Weil die Abweichungen von einer Kugel bereits bei einer Auflösung von 10 km deutlich werden. Eigentlich wird der Geoid für die meisten kommerziellen Zwecke zu einem Ellipsoid glattgestrichen.
Und wenn man noch genauer hinsieht und vor allem sich anschaut wie die Massenverteilung der Erde sich im Laufe der Jahre ändert, dann sollte man auch sehen, dass sich z.B. Nordeuropa bis zum heutigen Tag von der Eislast der letzten Eiszeit erholt und allmählich aus dem Erdmantel hervortaucht, in welche die Erdkruste durch das Eis mit roher Gewalt hineingedrückt wurde.
Diese postglaziale Landhebung sollte zu messbaren Anomalien im Schwerefeld führen. Bereits GRACE sollte diese messen. Wir sprechen hier von einer Landhebung von 3 mm pro 5 Jahre und der neue Satellit GOCE soll noch genauer vermessen. Die postglaziale Landhebung führt übrigens dazu, dass die Stadt Stockholm, deren Einwohner den Titel “Venedig des Nordens” für sich reklamieren, ironischerweise nach und nach trocken fällt. Falls jetzt nicht der Meeresspiegel zum Ausgleich durch andere Prozesse anwächst.
Bild: Landhebung in Stockholm.
————-
(1)
Hier sind auf der Mitte der Seite schöne Animationen zu finden, wie das aussieht mit Drehung und Trägheit: Rotational Motion of an Object around Its Three Principal Axes of Inertia
Das hier sollte Euch ein Gefühl dafür geben, dass es nicht egal ist, wie die Massen um eine Drehachse bei gleichem Gesamtgewicht verteilt sind.
Auf ähnliche Weise kann man auch herausfinden, ob ein Ei gekocht oder roh ist. Ein gekochtes Ei sollte sich leicht rotieren lassen. Ein rohes Ei kriegt man anfangs kaum in Gang, wenn man es dann aber doch ans Rotieren kriegt, dann hört es auch so schnell nicht wieder auf.
———–
Disclaimer:
Ja, ich hab die Herleitungen geschludert.
Ja, möglicherweise bin ich an einigen Stellen ungenau.
Es soll aber der Versuch sein, das Thema halbwegs korrekt und dabei möglichst anschaulich darzustellen. Weil die Konzepte, die hier dargestellt werden, in der Geo- und Planetenphysik zu den absoluten Grundlagen gehören. Wenn ich es einmal dargestellt habe, dann kann ich immer wieder drauf verweisen.

Kommentare (2)