Ich muss grinsen beim Schreiben dieser ersten Zeilen. Hochauflösungsmikroskopie ist mein Ding, ich habe in dem Bereich meine Dokorarbeit geschrieben, ich habe viele Freund*innen und Kolleg*innen, die in dem Bereich forschen – ach ich mag das Feld einfach, es hat mich von Anfang an fasziniert. Aber was das jetzt genau ist verrät dieses Wortungetüm leider noch nicht direkt, und eigentlich ist diese lange Aneinanderreihung von Buchstaben eigentlich auch nur eine verkürzte Bezeichnung. Richtig müsste es eigentlich Hochauflösungsfluoreszenzmikroskopie heißen, nur nennt es so niemand. Meistens spricht man von Super-Resolution als Oberbegriff, nicht nur weil die englische Bezeichnung irgendwie schmissiger klingt, sondern auch weil man in den meisten Fällen sowieso die englischen Begriffe im Kopf hat.
Also: Was ist Super-Resolution?
Der ein oder andere erinnert sich vielleicht an den Nobelpreis 2014 für Chemie. Nein? Der ging an zwei Amerikaner und einen Deutschen, William E. Morner, Eric Betzig und Stefan Hell für the development of super-resolved fluorescence microscopy, was übersetzt nicht anderes heißt als für „die Entwicklung hochaufgelöster Fluoreszenzmikroskopie“.
Es geht dabei immer um Mikroskopiemethoden, die mit Licht aus dem sichtbaren Teil des elektromagnetischen Spektrums funktionieren. Elektronenmikroskopie zählt nicht dazu, obwohl diese Technik die beste Auflösung hat. Allerdings ist die Elektronenmikroskopie auch recht beschränkt in dem was sie darstellen kann. Ein bisschen etwas darüber habe ich bereits unter Besuch bei Robert Mikroskopen aufgeschrieben.
Zurück zum sichtbaren Licht. Genau das stellt uns, durch seine Wellennatur, ein Hindernis in den Weg, wenn wir Mikroskopie machen wollen: Die Beugungsgrenze des Lichts. Dies allein ist schon eine spannende Geschichte für sich, und ein bisschen was davon habe ich bei Ernst Abbe war ein faszinierender Mensch aufgeschrieben. Für uns reicht es hier einfach zu wissen, das zwei Lichtpunkte nicht mehr von einander zu unterschieden sind, wenn sie zu eng zusammenstehen. Die Schwierigkeit besteht dann, wenn die gemessene Distanz der beiden Lichtpunkte zueinander unter der halben Wellenlänge der verwendeten Lichtquelle liegt; der sogenannten Beugungsgrenze.
Allerdings gibt es Möglichkeiten diese Beugungsgrenze zu umgehen. Aber wie immer im Leben: so etwas ist nicht umsonst. Man handelt sich andere Schwierigkeiten und Probleme ein, je nachdem welche Strategie man nutzt, um das Licht quasi auszutricksen. Für diese Strategien gibt es nicht wirklich treffende Oberkategorien – finde ich – daher hab ich meine eigene kleine Einteilung gewählt: mathematisch, physikalisch und chemisch.
Mathematische Überlistung
Das wohl prominenteste Beispiel hier wäre wohl die strukturierte Beleuchtung, auf Englisch Structured Illumination Micorscopy (SIM). Kurz und kompliziert gesagt: Durch Transformationen in den Frequenzraum von Bildern können Frequenzen unterhalb der Beugungsgrenze sichtbar gemacht werden. Kurz und einfach gesagt: Wir benutzen diese lustigen Muster in zwei überlappenden Geländern (Blick auf Autobahnbrücken z.B.) oder bei kleinkarierten Hemden im Fernsehen, um Dinge zu sehen die kleiner sind als die Beugungsgrenze. Diese Muster nennt man auch Moiré-Effekt.
Bei der strukturierten Beleuchtung regt man die Farbstoffe in einer Probe (siehe Das bringt Farbe ins Leben) mit einem engen Streifenmuster an, das sinusförmig ist. Dieses Muster verschiebt man einige Male senkrecht zur Streifenrichtung, dreht es um 60°, verschiebt wieder, dreht es ein letztes Mal um 60° und verschiebt wieder. Am Ende bekommt man so 15 Bilder, je fünf Bilder von kleinen Verschiebungen der jeweiligen Rotationen. Diese Bilder werden dann einer mathematischen Transformation in den Frequenzraum unterzogen, der sogenannten Fourier-Transformation.
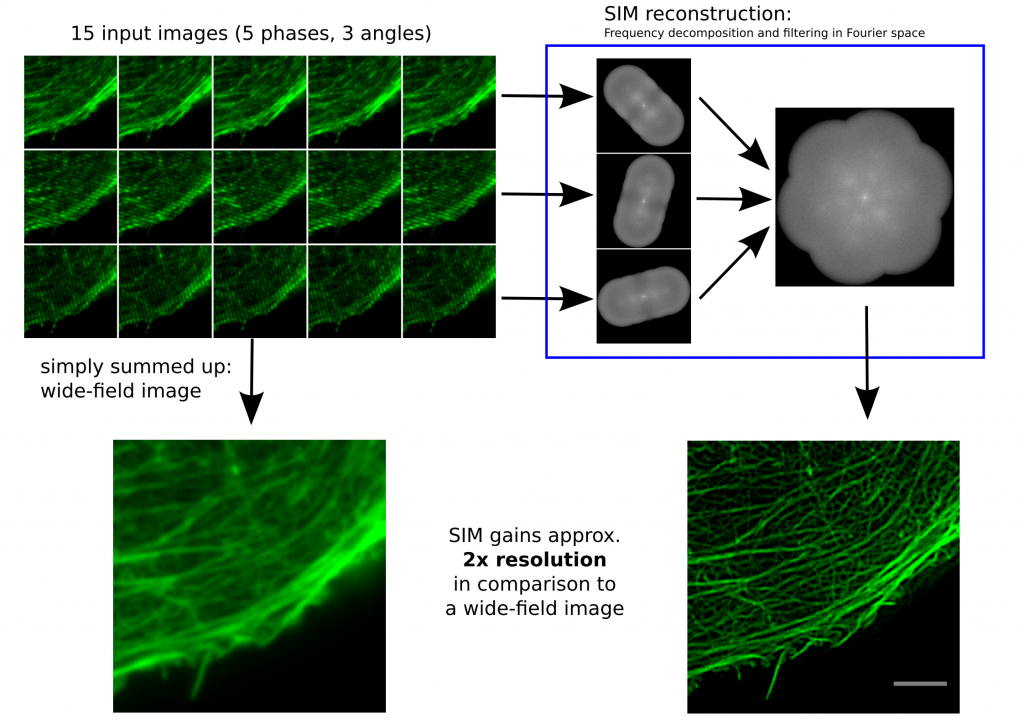
Funktionsweise SIM von Dr. Marcel Müller, Uni Bielefeld CC-BY-SA 4.0
Links, im Bild oben, sieht man 15 Bilder: die Rohdaten. Auf der rechten Seite kann man die Fouriertransformationen erkennen. Die drei „pillenfömigen“ Bilder sind die kombinierten Fouriertransformationen von den fünf Verschiebungen eines Winkels. In diesem Beispiel wurde Aktin angefärbt. In der Animation weiter unten, ist der eindimensionale Fall dargestellt. Die grauen Kästen stellen die markierten Strukturen in einer Probe dar, die blaue Linie ist das, was ein normales Fluoreszenzmikroskop sehen würde, die Sinusfunktion in türkis stellt die strukturierte Beleuchtung dar und in rot sind die Signale des SIM gezeigt. Man sieht, dass auf der linken Seite SIM einzelne Spitzen produziert, wohingegen im normalen Mikroskop (blau) keine getrennten Spitzen zu sehen wären.
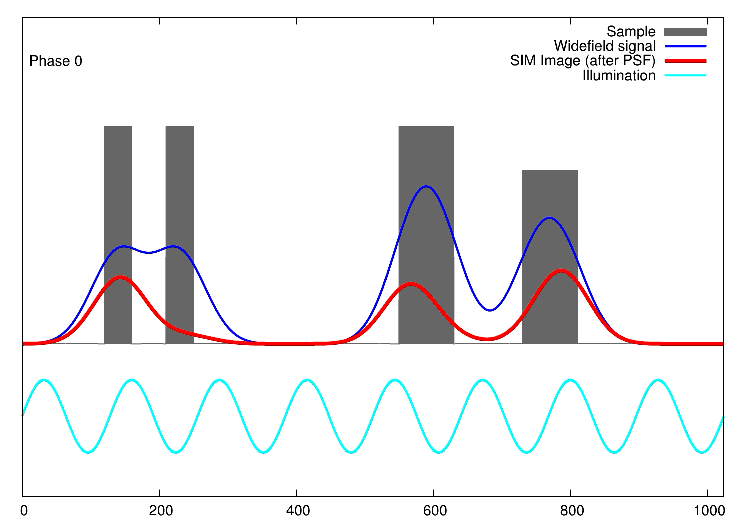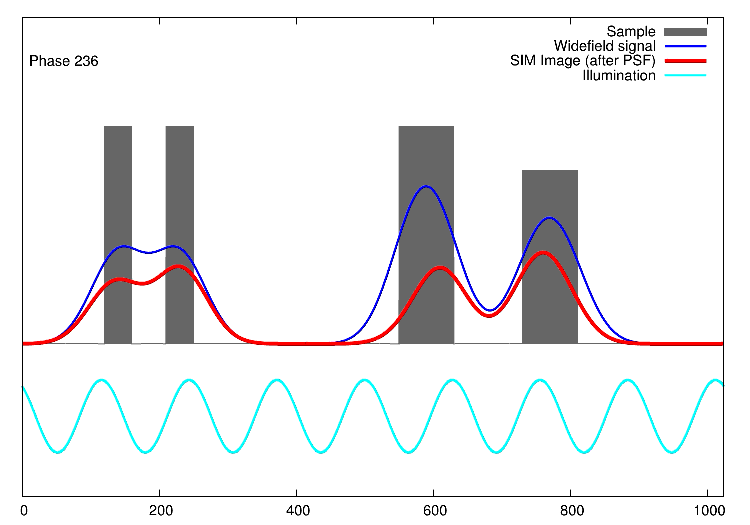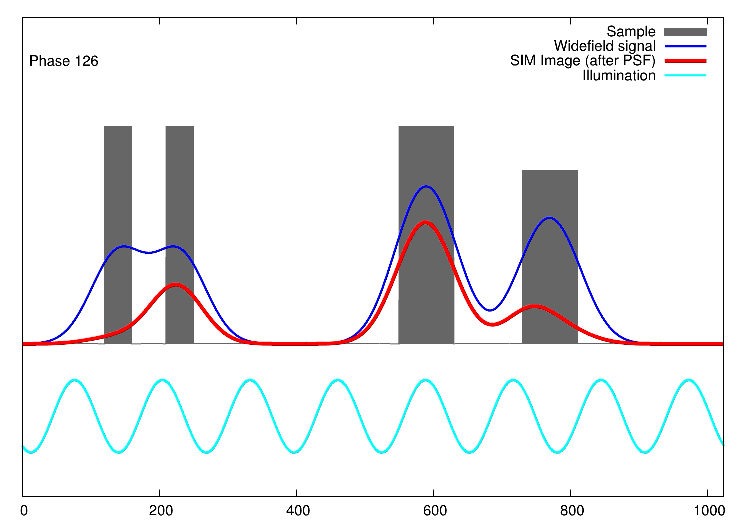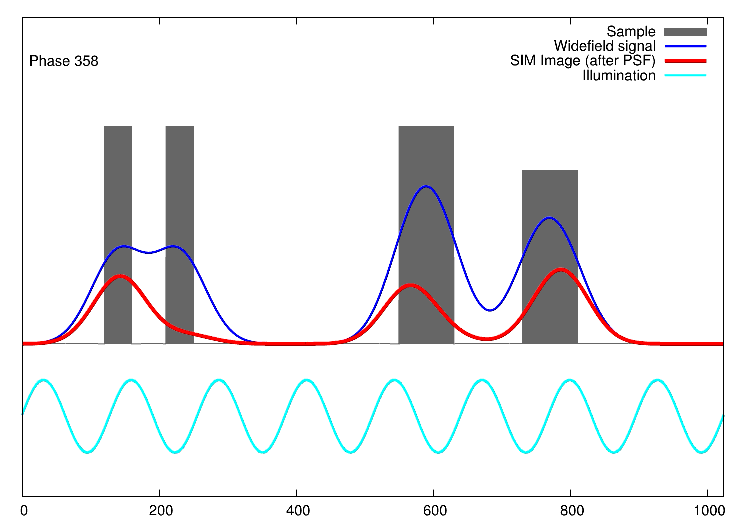
1D SIM von Dr. Marcel Müller, Uni Bielefeld CC-BY-SA 4.0

 orcid.org/0000-0003-0750-4757
orcid.org/0000-0003-0750-4757
Kommentare (11)