Ein Gastbeitrag von Philippe Leick
Verallgemeinerte Quantentheorie und Homöopathie
Zwölf Jahre ist es her, dass Harald Atmanspacher, Hartmann Römer und Harald Walach in Foundations of Physics eine Arbeit veröffentlichten (1), in der sie die Möglichkeiten von Verschränkungen auch außerhalb der engen Grenzen des quantenmechanischen Mikrokosmos betrachteten. In ihrem Artikel beschrieben sie zuerst den theoretischen Überbau, eine Verallgemeinerung der Quantenmechanik, und deuteten anschließend mögliche Anwendungen an, darunter auch die Homöopathie.
Damals wurde der Begriff der „schwachen“ Quantentheorie eingeführt (Weak Quantum Theory, oder WQT), da gewisse Randbedingungen im Vergleich zur physikalischen Quantenmechanik weniger stark sind. Mittlerweile wird insbesondere im deutschsprachigen Raum der Begriff der „schwachen Quantentheorie“ nur noch von Kritikern verwendet. Ihre Anhänger bevorzugen (möglicherweise aufgrund naheliegender und wenig schmeichelhafter Wortspiele) den passenderen Begriff der „Verallgemeinerten Quantentheorie“ (VQT), den ich auch in diesem Beitrag verwenden werde.
Kurz nach der Veröffentlichung der ersten Arbeit legte Harald Walach einen Artikel vor (2), in dem er, basierend auf der VQT und den Vergleich zur quantenmechanischen Teleportation, ein ausführliches Modell der Homöopathie beschrieb. Wenig später folgte ein weiteres, ebenfalls auf der verallgemeinerten Quantentheorie aufbauendes Homöopathie-Modell von Lionel R. Milgrom (3), welches nicht nur den Patienten und das homöopathische Mittel, sondern auch den praktizierenden Homöopathen mit einbezieht.
Beide Modelle versuchen zu erklären, warum placebo-kontrollierte, randomisierte und doppelblind durchgeführte klinische Studien (Randomized Controlled Trial oder RCT) der Homöopathie „überhaupt keine gute Idee“ sind (Walach). Die Homöopathie, die in der täglichen Praxis so beeindruckende Erfolge feiert, muss in solchen Studien scheitern, weil es zu einer Verschränkung zwischen den beiden Gruppen kommt, die mit dem Placebo bzw. dem richtigen Mittel behandelt werden. Die Ergebnisse der beiden Gruppe „verschmieren“ bis zur Unkenntlichkeit und es ist kein Unterschied mehr zwischen Homöopathie und Placebo erkennbar. Das Versagen der Homöopathie in RCTs ist demnach kein Indiz mehr für die fehlende spezifische Wirksamkeit der Intervention, sondern ein Beleg für die Richtigkeit der auf „verallgemeinerter Verschränkung“ basierenden Erklärungsansätze.
Mit Hilfe der verallgemeinerten Quantentheorie kippt eines der wichtigsten Argumente der Gegenseite scheinbar elegant um und wird zu einem Beleg für die Homöopathie. Vielleicht ist es deshalb kein Wunder, dass sie unter forschenden Komplementärmedizinern hohes Ansehen genießt. Die Originalarbeit (1) kommt laut Google Scholar jedenfalls auf beeindruckende 185 Zitate (Stand: 21.7.2013), und die Modelle von Walach, Milgrom und anderen werden in Fachzeitschriften wie Homeopathy immer wieder wohlwollend diskutiert. Dazu kommt natürlich noch die allgemeine Tendenz, alles unerklärliche mit der Quantenmechanik in Verbindung zu bringen.
Vor einigen Jahren habe ich mich sehr kritisch mit der verallgemeinerten Quantentheorie auseinandergesetzt (4)(5)(6). Der Ansatz, Phänomene außerhalb des eigentlichen quantenmechanischen Mikrokosmos mit mathematischen Modellen zu beschreiben, die eher an Quantenmechanik als an klassische Physik zu erinnern, ist natürlich legitim. Aber ohne physikalischen Kontext, ohne eindeutige Korrespondenz zwischen Modellgrößen und Realität sind solche Modelle nicht mehr als mathematische Spielereien. In Walachs und Milgroms Modellen sucht man vergeblich nach wissenschaftlicher Präzision. An keiner Stelle wird klar begründet, aus welchen Annahmen der Modellaufbau folgt oder warum nicht ein anderer, ebenso plausibler Ansatz gewählt wurde. Mit mathematischen Größen, deren physikalisches Pendant nur schwammig angedeutet wird, lässt sich auch deutlich „entspannter“ rechnen als mit klar definierten Größen (7). Analogien zur Quantenmechanik werden immer dann bemüht, wenn es gerade passend erscheint, aber ignoriert, wenn sie das eigene Konzept nicht stützen…
Ein ganz anderer Kritikpunkt ist die fehlende Wissenschaftlichkeit eines Ansatzes, der im Nachhinein alles (z.B. Misserfolge in RCTs) erklärt, aber keine überprüfbaren Vorhersagen macht. So hatte ich in einem Brief an Homeopathy (5) gefordert,
„[T]he real test of these models is not whether they explain previously known features of homeopathy, but whether they can be used to improve the design of experimental tests of homeopathy’s core hypothesis that high dilutions are different from appropriately prepared placebos.“
Von Walach und Milgrom gibt es Vorschläge, die strengen Regeln großangelegter RCTs für die Homöopathie-Forschung zu lockern. Sie sollte näher an der täglichen homöopathischen Praxis stattfinden. Unter solchen Umständen kann aber keine positive Studie Kritiker beeindrucken, die vom Placebo-Effekt und einer Fülle anderer systematischer Fehler wissen, die in unkontrollierten Studien kaum zu vermeiden sind (8)(9).
In der aktuellen Ausgabe von Homeopathy finden sich „in einem seltsamen Fall von Synchronizität“ (Herausgeber Peter Fisher im Editorial, (10)) gleich zwei Arbeiten, die zumindest teilweise auf der verallgemeinerten Quantentheorie aufbauen und Auswege aus diesem Dilemma vorschlagen.
Der erste Beitrag (11) stammt von Francis Beauvais, einem früheren Mitarbeiter von Jacques Benvéniste. Beauvais gibt freimütig zu, dass Benvénistes Versuche nie unter doppelblinden Bedingungen reproduziert werden konnten (12). Die Ursache sieht er mittlerweile in einer Art verallgemeinerter Verschränkungen zwischen aktiven und inaktiven Proben – dem gleichen Mechanismus, der auch RCTs homöopathischer Behandlungen zum Scheitern verurteilt. Basierend auf der schwachen Quantentheorie entwirft er ein einfaches Modell einer homöopathischen Doppelblindstudie. Nach einigen Rechenschritte wird eine kleine Veränderung des RCT-Protokolls vorgeschlagen, die Skeptiker kaum stören wird und sich ohne weiteres mit nur geringem Zusatzaufwand realisieren lässt. Beauvais hat hohe Erwartungen an seine Methode und schreibt in der Zusammenfassung:
„Comparing in situ randomization/unblinding vs. centralized supervision of clinical trials could be the equivalent of the Aspect’s [sic] experiment for quantum theories of homeopathy. Thus, positive results in homeopathy blind RCT using the in situ methodology would be not only a means to circumvent the gold standard, but also a very strong argument in favor of nonlocal theories for homeopathy.“
Zur Erläuterung: In den Experimenten von Alain Aspect et al. wurde die quantenmechanische Verschränkung zum ersten Mal nachgewiesen – diese Versuche und darauf aufbauende Verbesserungen gehören zu den wichtigsten Schlüsselexperimenten der modernen Physik, auch wenn der Nobelpreis dafür noch aussteht.
Ob Beauvais‘ Vorschlag ein Schritt in die richtige Richtung ist oder unter den gleichen Problemen leidet wie zahlreiche andere Beiträge aus Homeopathy kann nur eine detaillierte Analyse zeigen.
Beauvais’ Modell
Beauvais‘ Modell einer homöopathischen Doppelblindstudie basiert auf einem Mach-Zehnder Interferometer (MZI).
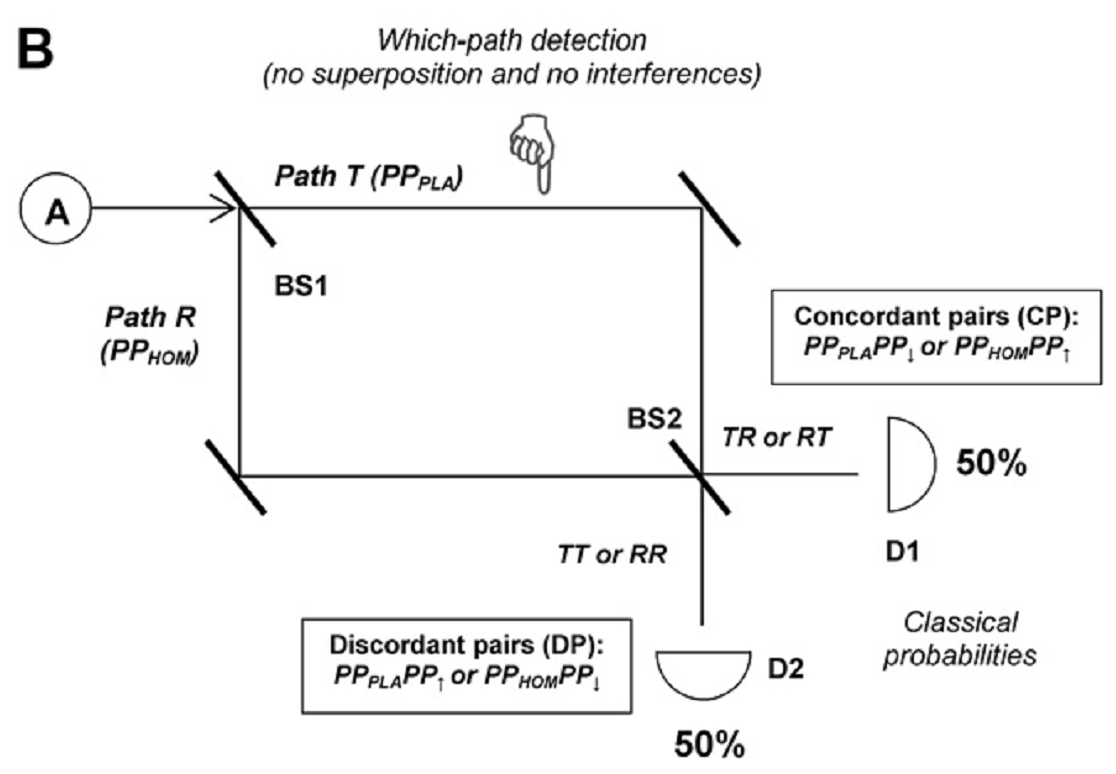
Licht kann darin über zwei Pfade zu zwei unterschiedlichen Detektoren gelangen. Betrachtet man das Licht als Welle, kommt es nach der Zusammenführung zu Interferenz zwischen den Teilen des Strahls, die auf unterschiedlichem Weg zum Detektor gelangt sind, und der obere der beiden Detektoren sieht 100% des Signals. Betrachtet man das Licht hingegen als Teilchen, gibt es keine Interferenz und beide Detektoren registrieren jeweils 50% des Signals. Interferenz erfordert kohärentes Licht. Jegliche Art von Messung, ob ein Photon den einen oder anderen Pfad genommen hat, zerstört diese Kohärenz. Eine sehr überraschende Eigenschaft des Mach-Zehnder-Interferometers ist, dass die Interferenz zwischen den beiden Teilstrahlen selbst dann nicht verschwindet, wenn die Lichtquelle soweit abgeschwächt wird, dass zu einem gegebenen Zeitpunkt nur ein einzelnes Photon im Interferometer sein kann. Wie beim bekannteren Doppelspalt-Versuch interferiert das Photon nicht mit einem anderen Photon, welches den anderen Pfad genommen hat, sondern mit sich selbst.
Beauvais‘ Analogie zwischen einer RCT und dem MZI beruht darauf, dass in beiden Fällen scheinbar zwei „Entscheidungen“ getroffen werden müssen:
Das Photon kann einen von zwei Pfaden nehmen und auf einen von zwei Detektoren fallen. Patient und Homöopath können der Verum- oder der Placebogruppe zugeordnet werden, und ihr Zustand kann sich verbessern oder nicht.
Statt vier möglicher Ergebnisse gibt es beim MZI jedoch nur zwei Detektoren. In seinem Modell muss Beauvais diesen Schritt erzwingen, indem er die Ergebnisse nur als „concordant pairs“ (CP) und „discordant pairs“ (DP) registriert – stimmt das Ergebnis mit der Erwartung überein, dass Verum zu Verbesserung führt und Placebo nicht (CP), oder ist es gerade umgekehrt (DP)? Ob das Homöopathikum nichts genutzt oder das Placebo geholfen hat, macht per Definition nun keinen Unterschied mehr.
Eine weitere, sehr wichtige Diskordanz: In der quantenmechanischen Beschreibung des Interferometers sind beide „Entscheidungen“ gleicher Natur. Das Photon kann von einem halbdurchlässigen Spiegel reflektiert oder durch ihn transmittiert werden. Es ist also ganz natürlich, dass diese Möglichkeiten miteinander verrechnet werden können. In der klinischen Studie gibt es eine zufällige Entscheidung, ob ein Patient Placebo oder Verum bekommt. Wie aber verhält es sich mit dem nächsten Schritt, nämlich der Entwicklung des gesundheitlichen Zustandes des Probanden? Warum nur zwei Möglichkeiten? Es könnte ihm nach Verabreichung des Mittels ja auch schlechter gehen, oder nur ein kleines bisschen besser… Wäre da nicht ein Kontinuum an Möglichkeiten (der Grad der Verbesserung) die bessere Beschreibung? Und wie will man das mit der Placebo/Verum-Entscheidung verrechnen? Misst man das überhaupt in den gleichen Einheiten?
Auf keine dieser Fragen geht Beauvais ein. Dabei bietet die Quantenmechanik durchaus komplexere Möglichkeiten als 2-Zustands-Systeme an; sie sind allerdings etwas weniger bekannt und nicht so einfach in der Anwendung.
Das nächste Fragezeichen stellt sich beim Ergebnis. Offensichtlich entspricht das Wellenbild des Interferometers dem homöopathischen Wunschzustand: Allen homöopathisch behandelten Patienten geht es besser, allen Placebo-Patienten hat die Scheinbehandlung nicht geholfen. Nach Beauvais‘ oben wiedergegebener Nomenklatur also 100% CP. Das Teilchenbild entspricht der „gescheiterten“ Studie: 50% CP und 50% DP bedeutet, dass es zwischen den Gruppen keinerlei Unterschied gibt.
Noch fehlt die Zuordnung zwischen möglichen Studienarten und dem Wellen- bzw. Teilchenbild. Auch dieser Schritt ist nicht ganz einfach, denn am Ende kommt keine Studie ohne Messung aus. Irgendwann muss ausgewertet werden, welche Patienten Placebo und welche das richtige Mittel bekommen haben. Beauvais identifiziert die „offene“ Studie, bei der Patient und Homöopath wissen, ob sie Placebo bekommen, mit dem Wellenbild bzw. mit 100% CP. Die „zentralisierte“ RCT – nur der Studienleiter kennt das „Messergebnis“ und weiß, wer Placebo bekommt und wer Verum – vergleicht er mit dem Teilchenbild.
Nach etwas Rechenarbeit erhält Beauvais trotz einer kleinen Ungenauigkeit (in einigen Formeln wird vergessen, dass Quantenmechanik auf komplexen Zahlen beruht) ein Ergebnis, das im Grunde nichts anderes ist als die allgemeinst mögliche Formulierung des quantenmechanischen 2-Zustands-Systems. Darin taucht ein „enigmatischer“ (Fisher) Parameter θ (theta) auf, der den Grad der Vermischung der Zustände CP und DP beschreibt. Beauvais spekuliert
„I did not hypothesise what θ stands for [… it] could summarize cognitive and mental phenomena as different as empathy, physician’s experience, expectation of patient and/or practitioner related to beliefs about treatment effectiveness and other cultural beliefs, Pavlovian conditioning, implicit learning, unconscious mechanisms and unknown mechanisms.“
und rechnet verschiedene Fälle vor. Warum er aus dem Fall θ = 0, wo es keinem Patienten (weder denen, die das Placebo erhalten haben, noch denen der Verum-Gruppe) besser geht, einen wichtigen Spezialfall konstruiert, konnte ich trotz mehrfacher Versuche nicht nachvollziehen. Den komplementären Fall θ = π/2 verschweigt er, womöglich weil die Erwähnung einer Situation mit Besserung aller Patienten – sowohl in der Placebo- als auch in der Verum-Gruppe – seinen Argumenten etwas Überzeugungskraft genommen hätte.
Bis jetzt erinnert Beauvais‘ Modell an eine etwas ältere Arbeit von Marcin Molski (13) , die unlängst von Ute Parsch auf dem Blog Beweisaufnahme in Sachen Homöopathie vorgestellt wurde (14) : Nach flüchtiger Lektüre mag der Anschein einer mathematisch stringenten Argumentation sich einstellen. Bei genauerer Analyse zeigt sich aber, dass die einzelnen Schritte nur locker aneinander gereiht, aber nicht auf zwingende oder besonders plausible Weise miteinander verbunden sind.
Geradezu bizarr ist aber eine Forderung an zukünftige Doppelblindstudien zur Wirksamkeit homöopathischer Präparate, die Beauvais aus seinen Überlegungen ableitet und als „ in situ randomization/unblinding“ bezeichnet. Arzt und Patient sollen zwei verdeckte Therapiesätze bekommen, wobei sich in einem Satz das Placebo und im anderen das echte, vermutlich individuell ermittelte Homöopathikum befindet. Selbstredend kennen weder Arzt noch Patient die Zuordnung. Anschließend losen sie aus, mit welchem Satz die Behandlung stattfinden soll. Nach Abschluss der Therapie und Bewertung des Wohlergehens des Patienten bekommen sie mitgeteilt, ob es sich um Placebo oder Verum gehandelt hat.
Eine „zentralisierte“, von Arzt und Patient unabhängige Studienplanung lehnt Beauvais ab, da sie zu der bereits angesprochenen Verschränkung zwischen den beiden Gruppen und damit zu einer „Verschmierung“ der Ergebnisse führt. Stattdessen entspricht d ie lokale (in situ) Messung von Behandlungsart (Verum oder Placebo) und Behandlungserfolg (Besserung oder nicht) dem Mach-Zehnder-Interferometer im gewünschten Wellenbild. Die beiden Versuchsarme interferieren irgendwie konstruktiv und führen in allen Fällen zum richtigen Versuchsergebnis (100% „concordant pairs“).
Wie sich in seinem Bild zentralisierte und in-situ-Versuchsdurchführung unterscheiden, erklärt Beauvais nicht. Auch den Grund, warum seine bevorzugte „in-situ-Messung“ dem quantenmechanischen Fall ohne Messung entspricht, bleibt er schuldig.
Weiter lässt sich einwenden, dass auch in-situ-Randomisierung nicht ganz ohne zentrale Versuchsplanung auskommt. Denn irgendwo muss bestimmt und notiert worden sein, welcher Behandlungssatz das Placebo und welcher das Verum enthält. Der Schlüssel muss von einer unabhängigen Person (oder einem Computer) verwaltet werden, da weder die behandelnden Ärzte noch ihre Patienten ihn kennen dürfen.
Etwas seltsam auch die Forderung, nach Studienende aufzudecken, ob der Patient Placebo oder Verum bekommen hat. Erstens ist dies bei RCTs durchaus üblich, zweitens kann es keinen Einfluss auf das Studienergebnis mehr nehmen, da zu diesem Zeitpunkt alle individuellen Ergebnisse bereits registriert wurden und nur noch ausgewertet werden müssen.
Trotz aller Kritik kann man Peter Fishers Editorial nicht widersprechen. Das vorgeschlagene Verfahren ist ohne besonderen Aufwand durchführbar und kann (sofern ich das zu beurteilen vermag) bei der nächsten Homöopathie-Studie angewendet werden. Die Aussagekraft der RCT sollte darunter nicht leiden. Aber die Argumente für diese Änderung des Versuchsdesigns sind dünn, einen Beitrag der verallgemeinerten Quantentheorie zu einem besseren Versuchsdesign für die Homöopathie kann ich nicht erkennen. Gute Gründe für weitere klinische Homöopathie-Studien sind ohnehin schwer zu finden , wie unlängst im GWUP-Blog und in der „ Homöopathie-Lüge “ von Christian Weymayr und Nicole Heißmann gezeigt wurde.
Ausblick
In der gleichen Ausgabe von Homeopathy schlägt Yannis Almirantis eine weitere Anpassung des Doppelblind-Protokolls vor (15) . Sein Vorschlag ist ebenfalls praktisch umsetzbar, wird am Rande auch mit der verallgemeinerten Quantentheorie begründet, und kann sogar mit Beauvais Anregung kombiniert werden. Die seltsamen Gedankengänge, mit denen er begründet wird, werde ich in Kürze in einem weiteren Beitrag vorstellen.
Literatur
- H. Atmanspacher, H. Römer, H. Walach: Weak Quantum Theory: Complementarity and Entanglement in Physics and Beyond, Foundations of Physics 32:3, 2002
- H. Walach: Entanglement Model of Homeopathy as an Example of Generalized Entanglement Predicted by Weak Quantum Theory, Forschende Komplementärmedizin und Klassische Naturheilkunde, 10, 2003
- L.R. Milgrom, Journeys in the Country of the Blind: Entanglement Theory and the Effects of Blinding on Trials of Homeopathy and Homeopathic Provings, Evidence-Based Complementary and Alternative Medicine 4(1):7-16, 2007
- P. Leick: Die „schwache Quantentheorie“ und die Homöopathie, Skeptiker 3/06, 2006
- P. Leick: Comment on: ‘‘Conspicuous by its absence: the Memory of Water, macro-entanglement, and the possibility of homeopathy’’ and ‘‘The nature of the active ingredient in ultramolecular dilutions’’, Homeopathy 97:51-52, 2008
- P. Leick: Das Gedächtnis des Wassers, Skeptiker 2/2008, S. 86-87
- D. Chrastina: Weak Quantum Theory isn’t that weak. Evidence-based Complementary and Alternative Medicine, E-Letters, 2008
- R. Barker Bausell: Snake Oil Science: The Truth about Complementary and Alternative Medicine, Oxford University Press, 2009
- I. Evans, H. Thornton, I. Chalmers and P. Glasziou: Testing Treatments. Better Research for Better Healthcare, 2nd edition, Pinter and Martin, 2011
- P. Fisher: Local, entangled or both?, Homeopathy 102:85-86, 2013
- F. Beauvais: A quantum-like model of homeopathy clinical trials: importance of in situ randomization and unblinding, Homeopathy 102:106-113, 2013
- F. Beauvais: Memory of Water and Blinding, Homeopathy 97:41-42, 2008
- M. Molski: Quasi-quantum model of potentization, Homeopathy 100:259-263, 2011
- U. Parsch: Diskussion zu ‘Quasi-Quantum Model of Potentization’ von Marcin Molski (Gastbeitrag von Ute Parsch), 5.7.2013, in N. Aust: Beweisaufnahme in Sachen Homöopathie
- Y. Almirantis: Homeopathy – between tradition and modern science: remedies as carriers of significance, Homeopathy 102:114-122, 2013



Kommentare (56)