Letzte Woche hat Florian sich Gedanken zur Flachen Erde und vor allem den Vertretern dieser doch etwas in die Jahre gekommenen Vorstellung, wir lebten nicht auf einer Kugel, sondern einer wie auch immer geformten flachen Scheibe gemacht. Es ist schon erstaunlich, dass auch in 2017 noch Menschen davon überzeugt sind. Es ist noch viel erstaunlicher, wie viel Zeit und Energie so mancher darauf verwendet. Die Flache Erde ist aber eigentlich nur was für Anfänger – da draußen gibt es noch interessantere Ideen: Die Erde ist nämlich nicht einfach nur flach, sie ist konkav! Ja, richtig gelesen – wir befinden uns nicht auf der Außen-, sondern der Innenseite einer Kugel. Wir leben in der Hohlen Erde.
Die Idee ist nicht ganz so alte wie die Flache Erde, aber es hat ja auch eine Weile gedauert, bis die Menschen überhaupt die grundsätzliche Form unserer Heimatwelt enträtselt hatten. Und sehr lange war ja gar nicht klar, was diese komischen Lichter am Himmel sind oder wie die Erde von oben wirklich aussieht. Für eine gewisse Zeit mag der Innenweltkosmos sogar nicht unplausibler gewesen sein, als die anderen Weltbilder. Genies haben für ihn argumentiert.
Richtig rechnen reicht nicht
Der vielleicht interessanteste Aspekt der Hohle-Welt-Lehre ist, dass im Gegensatz z.B. zur Flachen Erde mit den Beobachtungen konsistente mathematische Beschreibungen unserer Welt und was sich drin bewegt möglich sind. Gerade weil in der Innenweltkugel nur sprichwörtlich “die Seiten vertauscht” sind, von der aus wir das Weltall betrachten. Das ist doch mal interessant – und ein schönes Beispiel dafür, dass Naturwissenschaft eben mehr heißt, also Formeln suchen und Werte einsetzen. Dass sich das so rechnen lässt, als lebten wir in einer Innenwelt heißt nicht, dass die beiden Weltbilder nicht unterscheidbar wären – es verdeutlicht aber, dass Naturgesetze auf viele Arten ausgedrückt werden können.
Wenn man eine Hypothese anbietet, dann sollte man idealerweise nicht nur den richtigen mathematischen Formalismus anbieten, sondern auch einen Mechanismus, der die Beobachtungen erklärt. Den nennen wir dann üblicherweise Naturgesetz. Wenn man nichts weniger als die ganze Welt ganz anders als üblich erklären will, dann muss man nichts weniger als alle bekannten Naturgesetze ganz anders als üblich formulieren. Und an dieser Stelle hakt auch die mathematisch korrekte Version der Hohle-Welt-Lehre gewaltig.
Zum Beispiel müsste man annehmen, dass sich die Länge eines Stabes, der Senkrecht auf der Weltachse steht ändert, wenn er entlang der Weltachse bewegt wird, sich also sein Abstand zum Zentrum ändert. Das muss so sein, denn sonst wären z.B. die Existenz des Mondes und der Sonne, die ja schon von menschengemachten Sonden besucht wurden mit ihrer beobachteten Größe, in einer Kugel von gerade mal 6.370 km Radius nicht erklärbar. Allerdings wäre diese Längenänderung nur von einem Gott, der die Welt von außen, im Sinne Kants die Welt an sich sieht, feststellbar. Ein Innenweltler würde davon nichts merken, weil ja auch alle seine Maßstäbe und Messgeräte der Änderung unterworfen sind.
Dito die Lichtgeschwindigkeit: Ein Licht- oder Funksignal, das in Richtung Zentrum geschickt wird, muss in Bezug auf den Beobachter auf der Erde seine Geschwindigkeit anpassen, denn sonst hätte es die Kugel in rund 40 ms durchquert. Das ist nicht das, was wir beobachten.
Diese Beispiele sollen den interessanten Fall verdeutlichen, dass man wunderbar rechnen kann, ohne zu physikalisch sinnvollen, d.h. überprüfbaren Ergebnissen zu kommen. Und ohne erklären zu müssen, was eigentlich die Ursache der Beobachtung ist. Wenn man die Behauptung aufstellt, dass Strecken oder die Lichtgeschwindigkeit sich in Abhängigkeit vom Abstand zum Zentrum ändern, dann muss man das mit sehr guten Argumenten untermauern. Vor über Hundert Jahren hat schon mal jemand etwas ähnlich exotisches behauptet, nämlich, die Vakuumlichtgeschwindigkeit sei in allen Bezugssystemen gleich. Er hatte zu seiner Zeit (und seine Nachfolger haben heute immer noch) immer wieder Probleme, diese Behauptung zu verteidigen. Aber er konnte es eben und wurde durch Beobachtungen unterstützt. Deswegen hat er sich auch durchgesetzt. Die Innenweltler sind davon noch weit entfernt. Sie haben keinen Einstein in ihren Reihen.
Es gibt noch viel mehr solche Fälle: Die Aberration des Lichtes, die Beobachtungen, die die SRT stützen, die Expansion des Raumes, Messung von Erdbeben auf der anderen Seite des Globus’…
Natürlich haben auch die Vertreter des Innenweltkosmos immer nach Beweisen für ihre Hypothese gesucht…
Die Naples-Landvermessung
Ein bisschen was zur Vorgeschichte: In den 1870 Jahren gründete Cyrus Teed, ein Arzt aus dem Staat New York, auf Anraten höherer Mächte eine religiöse Gemeinde und baute eine eigene Vorstellung des Kosmos auf, die er Cellular Cosmology nannte und die dem Innenweltbild entspricht. Mitte der 1890er Jahre stieß der Erfinder Ulysses Grant Morrow, der unabhängig von Teed ähnliche Gedanken hegte, zu der Gruppe und überlegte, wie man wohl das Weltbild beweisen könnte. Als ich zum ersten Mal davon hörte, hielt ich die ganze Geschichte ja für einen Scherz, aber der Herr Morrow scheint es tatsächlich ernst gemeint zu haben.
Morrow dachte sich, dass es doch möglich sein sollte, die Frage zu klären, indem man eine lange, gerade Strecke konstruiert, die senkrecht auf dem Erdradius steht. Bei ausreichender länge sollte sich die Strecke entweder vom Erdkreis entfernen – dann wäre bewiesen, dass wir auf einer konvexen Erde leben – oder sich ihm annähern – dann wäre bewiesen, dass wir in einer konkaven Erde leben. Der Erfinder machte das so: er konstruierte ein Messgerät, das er Rectilineator nannte, im Deutschen meist sinngemäß übersetzt mit Geradstreckenverleger. Das Gerät bestand aus einer Reihe senkrechter Pfosten an denen rechteckigige Elemente angeschlagen werden konnten, die die Funktion von Messnormalen erfüllten. Jedes Element war 12 Fuß (3,66 m) lang und 4 Fuß (1,22 m) hoch , gefertigt aus Mahagoni. Die Elemente waren für zusätzliche Stabilität kreuzweise mit Stahlstangen versperrt und an den Enden mit Messingplatten für exakte Ausrichtung und Verbindung versehen. Im Prinzip sollte es mit so einer Anordnung möglich sein, nach exaktem Ausrichten des ersten Elementes auf eine Bezugsebene durch Anfügen weiterer Elemente eine gerade Strecke zu verlegen. Sollten wir tatsächlich auf der Innenseite einer Kugel leben, würde die Gerade irgendwann die Kugeloberfläche schneiden. Der Geradstreckenverleger sollte also die Konstruktion einer Sehne im Erdkreis ermöglichen. Prinzipiell ist das eine pfiffige Idee.
Ich habe auf die Schnelle kein freies Bild des Rectilieators gefunden. Aber natürlich findet man was, wenn man danach sucht (Aber Achtung: Die Seiten, die man findet, haben’s in sich! Google at your own risk).
Das Experiment sollte 1897 in Naples, Florida stattfinden und als Naples Geodetic Survey (Naples-Landvermessung) in die Geschichte eingehen. Es dauerte 10 Wochen und ist hier ausführlich beschrieben. Im Ergebnis dokumentieren die sorgfältig geführten Aufzeichnungen die Verlegung einer geraden Strecke, die sich messbar und in der richtigen Größenordnung dem Erdradius annähert – Das Innenweltbild war bewiesen.
War es das?
Der Erdradius beträgt etwa 6.370 km Vorausgesetzt das Experiment wird in Nord-Süd-Richtung durchgeführt. Der kleinste Erdradius bei 26° nördlicher Breite liegt bei ca. 5.730 km. Abb. 2 zeigt ein Element in vereinfachter Darstellung. die grünen Linien sind zwei Lote, die vom Zentrum des Erdkreises ausgehen und das Element an seinen Außenkanten schneiden sollen. Die orangen Linien zeigen den Abstand voneinander an. Wie man sieht, weichen die Abstände nur 700 bzw. 800 nm (ja, Nanometer) voneinander ab. Um den Punkt zu verdeutlichen nicht wirklich ein Unterschied – nehmen wir für das Folgende zu Morrows Gunsten ruhig 1.000 nm an, die zu unterbieten sind.
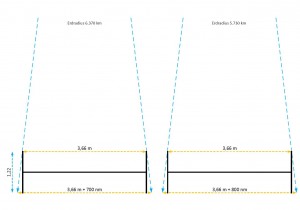
Fällt man zwei Lote im Abstand von 6.370 km über ein Element des Geradstreckenverlegers, dann weicht der Abstand der Lote oben und unten gerade mal um 700 nm voneinander ab.
Will man damit auch nur eine einigermaßen genaue Messung durchführen, muss die Fertigungstoleranz viel viel kleiner sein. Lassen sich die Elemente mit der Technik von 1890 mit der nötigen Präzision fertigen? Jedes Element wurde über 250 Mal aus- und eingebaut, ausgerichtet und bewegt. Haben sie sich dabei gar nicht abgenutzt? Wenige Nanometer Abnutzung hätten schon gereicht, die Ergebnisse zu verfälschen. Morrow nimmt ± 2 % Messfehler an: 20 nm bzw. 10 nm in jede Richtung. So viel und nicht mehr dürfen die Seiten von der perfekten Parallelität abweichen. Gewöhnlicher Staub bildet schon Partikel in der Größenordnung 10.000 nm.
Das Material ist im Wesentlichen Mahagoni. Holz hat einen sehr kleinen Ausdehnungskoeffizienten von etwa 5 x 10-6 pro Kelvin. Damit sich ein 1,22 m bzw. 3,66 m langes Objekt aus Holz um 20 nm dehnt oder staucht, bedarf es einer Temperaturänderung von ca. 80 bzw. 28 mK (ja, Millikelvin). Waren alle Elemente unter freiem Himmel und mit allen Witterungseinflüssen über den gesamten Zeitraum so gleichmäßig temperiert? Zusammen mit den Stahlverstrebungen ergibt sich ein Verbundstoff mit allen unschönen Eigenschaften, wie unterschiedlichen Elastizitätsmodulen, Festigkeit, Ausdehnungskoeffizienten (wer schon mal mit Stahl-Email-Rohr gearbeitet hat, weiss vielleicht wovon ich spreche) und damit Spannungen/Verwindungen bei Temperaturwechseln oder der Montage/Demontage. Verhältnismäßig kleine Temperaturschwankungen bringen alles durcheinander. Um Fehler in der ursprünglichen Parallelität auszugleichen wurde jedes Element zwischen Aus- und Einbau auf den Kopf gestellt. Das scheint eine gute Idee, um Fehler bei Bau und Kalibration auszugleichen. Allerdings schützt das nicht gegen die kleinen Längenänderungen durch Temperaturschwankungen.
Das erste Element muss sehr genau auf die Bezugsebene ausgerichtet sein. Dazu wurde mit erheblichem Aufwand die exakte Höhe über dem Meer (was schon allein schwer genug ist) bestimmt und das Element dann mit einer 12 Fuß (3,66) m langen, Quecksilber gefüllten Libelle, einer Alkohol gefüllten Libelle und einem Senkblei ausgerichtet. Jedes Element war 3,66 m lang. Erinnern wir uns an die Fertigungstoleranz: 10 nm darf jedes Ende eines Elements von der idealen Senkrechten abweichen, um Morrows geforderte Genauigkeit zu erreichen. Mit optischen Messgeräten dieser Zeit kann man keine Strukturen auflösen, die kleiner als ca. 500 nm sind – selbst bei überragenden Fähigkeiten der Versuchsmannschaft wäre die korrekte Ausrichtung reines Glück gewesen.
Das und noch einiges mehr macht das Experiment gelinde gesagt unplausibel. Was können die Gründe dafür sein, dass das Ergebnis so gut gepasst hat? Immerhin hat Morrow viel Aufwand betrieben, um allem einem seriösen Anstrich zu geben: Die Messungen wurden mehrfach durchgeführt und sorgfältig dokumentiert, ein unabhängiges Komitee wachte über den Verlauf. Eine einfache Fälschung kommt also schwerlich in Betracht. Die Gründe müssen subtilerer Natur gewesen sein.
Zunächst gibt es keinen perfekten Festkörper. Alle Körper sind in gewisser Weise flexibel. Jeder Körper, der wie die Geradstreckenverleger-Elemente an zwei Festpunkten befestigt ist, wird links und rechts dieser Punkten absacken – und sei die Höhe noch so klein. Insbesondere wirkt wegen der Gravitation die Absackung immer nach unten, die “gerade” Strecke hat also immer die Tendenz, nach unten zu zeigen und damit das Innenweltbild zu stützen. Diese Effekte waren 1897 schon bekannt und hätten herausgerechnet werden können – Morrows Aufzeichnungen geben dafür keinen Anhaltspunkt. Aber allein damit ließe sich schon eine Menge erklären: Die ganze Zeit wären die Experimentatoren der Meinung, eine gerade Strecke zu verlegen, obwohl sie in Wirklichkeit leicht nach unten gebogen war. Aber auch dafür ist die prinzipielle Ungenauigkeit des Geradstreckenverlegers eigentlich zu groß. Außerdem würde damit nicht erklärt werden, warum die Ergebnisse gerade den Erwartungswert wieder spiegelten und nicht etwas gänzlich anderes. Oben habe ich geschrieben, dass Morrow erwartete, dass die Messungen mit 2 % Genauigkeit durchgeführt werden konnten. Da habe ich zu Morrows Gunsten etwas Wichtiges unterschlagen: Die 2 % beziehen sich nicht auf die Messung an sich, sondern auf die Genauigkeit, mit der aus den Daten nach Extrapolation auf den Erdradius geschlossen werden kann. Um diesen mit 2 % Fehler ermitteln zu können, muss die Einzelmessung noch viel genauer durchgeführt werden! Aber das ist gar nicht mal so sehr der Punkt: Viel wichtiger ist die Erwartung bestimmter Ergebnisse durch Morrow und sein Team.
Wenn man Experimente wie dieses durchführt, dann epfiehlt es sich, die Daten erst auszuwerten, wenn sie vollständig gesammelt sind und die Auswertung nicht demselben Team zu überlassen, das die Daten gesammelt hat. Und das Team, das die Daten sammelt sollte auf keinen Fall vorher die Erwartungswerte sehen! Damit minimiert man die Gefahr des Expectation Bias, also der (möglicherweise unbewussten) Beeinflussung der dokumentierten Ergebnisse durch die Erwartungshaltung des Experimentators. Klingt irgendwie vertraut. Hand aufs Herz: Wer hat nicht mal mit Leuten zusammengearbeitet, die bereit waren, Ergebnisse übertrieben positiv zu interpretieren, weil man ja weiss, was rauskommen muss? Warum sollten gerade Menschen mit einer besonderen Überzeugung davor gefeit sein?
Nicht totzukriegen – das Innenweltbild heute
Man sollte meinen, dass in 2017 jeder schon mit einfachen Überlegungen zum richtigen Ergebnis kommen sollte. Aber das sollte man auch von der Flachen Erde meinen. Wenn man so ins Internet guckt, findet man sehr viele Seiten, die sich exklusiv mit dem Innenweltkosmos, seiner rechnerischen Beschreibung und den Experimenten dazu beschäftigen. Und ich kann mir nicht vorstellen, dass sich daran wirklich was ändert. Ich denke, viele Leute machen im Laufe ihres Lebens eine Phase des Suchens durch, in der sie alles in Frage stellen, was man ihnen beigebracht hat. Auch und insbesondere die Ergebnisse der Naturwissenschaft. Einige bleiben darauf hängen. Eigentlich schade. Die meisten erkennen aber irgendwann, dass das was in den Büchern steht doch so falsch nicht sein kann und wenden sich wieder von den exotischen Ideen ab. Wenn das stimmt, dann bedeutet es, dass die meisten Leute sich doch irgendwann die Hörner abstoßen, aber es heißt leider auch, dass es zu jedem Zeitpunkt genügend Menschen gibt die bereit sind, auch den größten naturwissenschaftlichen Unsinn zu glauben.
Update, 14.05.2017: Da hat sich ein kleiner Fehler eingeschlichen: 2 % von 1.000 nm sind 20 nm. Das hat ein paar Korrekturen nötig gemacht, die das Experiment noch unplausibler machen als es ohnedies schon war.

Kommentare (31)