So wie die Neuronen die zentralen Bestandteile des Nervensystems sind, stellen künstliche Neuronen die Grundbausteine eines KNN dar. Im Prinzip sind Neuronen und künstliche Neuronen ähnlich aufgebaut; beide besitzen viele Eingänge für Reize (die Dendriten beim Neuron), einen Körper, welcher die Reizverarbeitung vornimmt (der Zellkörper) sowie einen Ausgang, über welchen das Ergebnis der Reizverarbeitung an andere (künstliche) Neuronen verteilt wird (das Axon im Neuron). Bildlich kann ein künstliches Neuron folgendermaßen dargestellt werden:
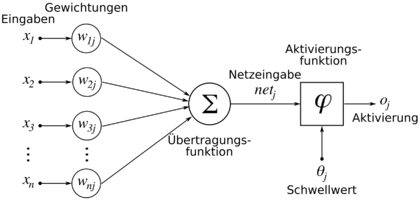
Ein künstliches Neuron (Quelle: Wikipedia)
Die Eingaben x1 bis xn entsprechen dabei den Dendriten im Neuron. Wir erinnern uns: die Länge eines Dendrits (die Entfernung seiner Synapse zum Axonhügel) bestimmt den Einfluss des Reizes, der über diesen Dendriten kommt, auf das gesamte Erregungspotential. Dies wird in einem künstlichen Neuron über die Gewichtung w abgebildet; je höher der Wert der Gewichtung, desto größeren Einfluss hat die Eingabe des zugehörigen Eingangs. Die Übertragungsfunktion in der Abbildung stellt gewissermaßen das Äquivalent zum Erregungspotential dar, da hier die ankommenden Signale entsprechend ihrer Gewichte aufsummiert werden. Der Schwellwert entspricht dementsprechend dem Schwellenpotential im biologischen Neuron und die Aktivierung beziehungsweise die Ausgabe stellt das Axon dar.
Eine Besonderheit stellt dagegen die Aktivierungsfunktion dar. Ein natürliches Neuron arbeitet nach dem Alles-oder-nichts-Prinzip, das heißt, dass bei Überschreitung des Schwellenpotentials ein festes, immer gleiches Aktionspotential erzeugt wird. Künstliche Neuronen können nach diesem Prinzip arbeiten, aber ebenso nach anderen; die Aktivierungsfunktion definiert hierbei, welche Ausgabe bei welcher Eingabe in Abhängigkeit des Schwellwertes generiert wird.
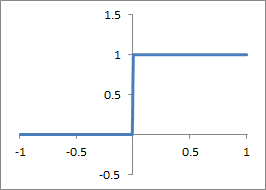
Eine häufig verwendete Aktivierungsfunktion ist eine Sprungfunktion, und zwar die sogenannte Schwellenwertfunktion. Diese bildet das Verhalten realer Neuronen nach, da eine konstante Ausgabe erzeugt wird, sobald die Eingabesignale den Schwellwert übersteigen. Weitere mögliche Aktivierungsfunktionen sind lineare und stückweise lineare Funktionen, deren Ausgabe lineare von der Eingabe abhängt (das heißt, bei doppelt so großem Eingabewert ist die Ausgabe auch doppelt so groß) und die ebenfalls relativ häufig verwendeten Sigmoidfunktionen mit einer ungleichmäßigen Abhängigkeit zwischen Eingabe und Ausgabe. Untenstehende Abbildungen zeigen drei mögliche Aktivierungsfunktionen anhand eines Funktionsgraphen; auf der x-Achse findet sich hierbei der aufsummierte und gewichtete Eingabewert, auf der y-Achse kann der zu dieser Eingabe generierte Ausgabewert abgelesen werden. Am Beispiel der Sprungfunktion bedeutet das, dass die Funktion solange den Wert 0 generiert, wie die Eingabe kleiner oder gleich 0 ist (siehe dazu auch die Anmerkung unter den Bildern); sobald die Eingabe aber größer als 0 wird, generiert die Funktion einen konstanten Wert von 1.
Aktivierungsfunktion: Sprungfunktion
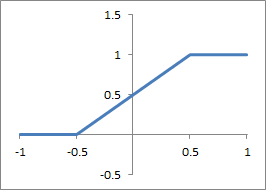
Aktivierungsfunktion: stückweise linear
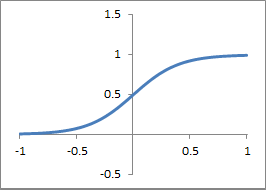
Aktivierungsfunktion: Sigmoid
In den drei Abbildungen ist jetzt jeweils der Schwellwert noch nicht berücksichtigt worden; dies lässt sich ziemlich einfach erreichen, indem die Kurve einfach nach links (niedrigerer Schwellwert) oder rechts (höherer Schwellwert) verschoben wird. Alternativ (mathematisch äquivalent) kann der Schwellwert natürlich auch einfach von der aufsummierten Eingabe abgezogen werden – das führt zum gleichen Ergebnis.
Es fällt übrigens auf, dass die Eingaben auch negativ sein können. In künstlichen Neuronen wird das erreicht, indem das Gewicht einer Eingabe ebenfalls einen negativen Wert erhält. Auch dafür gibt es eine Entsprechung in echten Neuronen, da bestimmte Synapsen nämlich ein hemmendes statt ein aktivierendes Potential hervorrufen können.
So, damit haben wir eine parallele zwischen biologischen und künstlichen Neuronen hergestellt (letztere können übrigens rein virtuell im Computer, aber auch als echte mechanische Bauteile existieren). In der Theorie könnte man sich nun vorstellen, dass einfach ganz viele künstliche Neuronen hergenommen und – ähnlich einem Gehirn – zusammengeschaltet werden können und schon hat man sich ein eigenes Gehirn gebaut. Ganz so einfach funktioniert das natürlich aber nicht; wie nun aber künstliche neuronale Netze genau eingesetzt (und vor allem, wie sie erzeugt) werden, erzähle ich im nächsten Artikel.

Kommentare (14)