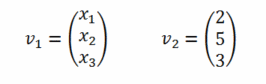Die Rechenregeln für Vektoren sind relativ einfach: die Addition zweier Vektoren erfolgt durch elementweises addieren der einzelnen Vektor-Positionen; die Multiplikation mit einem Skalar erfolgt, indem jedes Element des Vektors mit dem Skalar multipliziert wird. Zusätzlich gibt es noch das sogenannte Skalarprodukt zweier Vektoren, bei dem die Elemente beider Vektoren paarweise multipliziert und die Ergebnisse aufaddiert werden (das Ergebnis ist also eine Zahl, kein Vektor), sowie das Kreuzprodukt mit einer etwas komplexeren Berechnungsregel, wobei das Ergebnis des Kreuzprodukts zweier Vektoren immer ein Vektor ist, der senkrecht auf beiden steht (eine in der Computergrafik sehr oft benötigte Rechenoperation).
Eine Matrix ist – grob gesagt – ein Vektor mit (potentiell) mehr als einer Spalte; konsequenterweise werden sie auch ähnlich notiert, in etwa so:
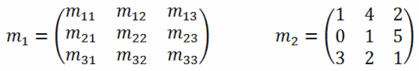
Auch für Matrizen gibt es natürlich Rechenregeln; die für die Computergrafik relevanten sind vor allem die Multiplikation zweier Matrizen sowie die Multiplikation einer Matrix mit einem Vektor (der ja im Grunde nur eine Matrix mit einer Spalte ist). Zwei Matrizen können miteinander multipliziert werden, wenn die erste Matrix genauso viele Spalten wie die zweite Zeilen hat; formal ausgedrückt: eine l×m-Matrix kann mit einer m×n-Matrix verrechnet werden, wobei das Ergebnis eine l×n-Matrix ist. Dies geschieht, indem die Ergebnismatrix nach folgender Formel aufgebaut wird (multipliziert werden hier die Matrizen a und b):
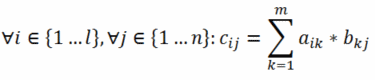
Die Multiplikation einer m×m-Matrix mit einer m×1-Matrix (einer Matrix mit einer Spalte – also ein Vektor) ist demzufolge wieder eine m×1-Matrix, also ein Vektor. Matrizen können in der Computergrafik dazu benutzt werden, um sogenannte Transformationen mit Hilfe von Transformationsmatrizen zu beschreiben. Eine Transformation bezeichnet dabei die Verschiebung eines Punktes nach einem gewünschten Schema und wird erreicht, indem der Vektor des zu transformierenden Punktes mit der passenden Transformationsmatrix multipliziert wird. Die Multiplikation zweier Transformationsmatrizen führt dagegen zu einer Matrix, welche die aufeinanderfolgende Durchführung der beiden Einzeltransformationen beschreibt.
Diese Mittel reichen bereits, um die beschriebene Projektion von Punkten durchzuführen. Die darzustellenden Punkte der Szene werden dabei zunächst einfach über Vektoren beschrieben; da wir dreidimensionale Punkte betrachten, haben die Vektoren auch entsprechend drei Werte. Zur Durchführung werden nun noch zwei Matrizen benötigt.
Die erste ist die sogenannte View Matrix, welche einen Punktes aus dem Weltkoordinatensystem (sprich: dem Koordinatensystem der Szene) in das Kamerakoordinatensystem (also in ein Koordinatensystem aus Sicht der Kamera) überführt. Praktisch kann man sich das folgendermaßen vorstellen: im Weltkoordinatensystem liegen die einzelnen Punkte beliebig im Raum verteilt; auch die Kamera ist in diesem System an einer beliebigen Stelle zu finden. Im Kamerakoordinatensystem bildet die Position der Kamera dagegen den Ursprung des Koordinatensystems, welches zudem noch entsprechend der Kameraausrichtung rotiert ist (so dass z.B. die Z-Achse im Kamerakoordinatensystem immer in Blickrichtung der Kamera, die X-Achse nach rechts und die Y-Achse nach oben zeigt). Bildlich dargestellt könnte eine derartige View Transformation also so aussehen (mit Objekten anstelle von Punkten zur besseren Verdeutlichung):
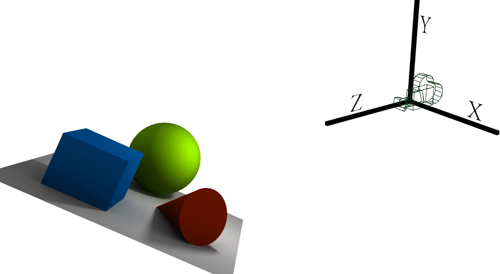
Die zweite benötigte Matrix zur Durchführung der Projektion ist die Projection Matrix (deutsch Projektionsmatrix); sie projiziert einen dreidimensionalen Punkt auf eine zweidimensionale Fläche. In der Computergrafik heißt das, dass die dreidimensionalen Punkte im Kamerakoordinatensystem (also aus Sicht der Kamera) auf zweidimensionale Koordinaten abgebildet werden, die ihrer Position auf dem Bildschirm entsprechen. Die Projektion kann dabei auf unterschiedliche Arten erfolgen, insbesondere kann eine Parallelprojektion oder eine perspektivische Projektion durchgeführt werden (für Details bitte hier schauen).
Das Ergebnis der Verrechnung eines Punktes im Kamerakoordinatensystem mit der Projection Matrix kann also direkt in den Backbuffer gezeichnet werden; fast zumindest. Aufmerksame Leser werden sicherlich bemerkt haben, dass das Ergebnis der Multiplikation einer 3×3-Matrix mit einer 3×1-Matrix (einem Vektor) ja wieder eine 3×1-Matrix, also ein Vektor mit 3 Elementen, ist – benötigt werden aber nur 2 Werte (nämlich die x- und y-Position auf der zweidimensionalen Fläche). Die ersten beiden Werte im Ergebnisvektor entsprechen nach der Projektion auch tatsächlich den
gesuchten Positionen; der dritte Wert dagegen gibt die sogenannte Tiefe des Punktes auf der zweidimensionalen Fläche an, kann also benutzt werden, um zu bestimmen, wie weit ein Punkt relativ zu anderen Punkten von der Kamera entfernt war – das ist zum Beispiel für Überdeckungstests wichtig, aber dazu vielleicht in einem späteren Artikel mehr.
Kommentare (13)