Alle Dreiecke, die sich außerhalb des Frustums befinden, müssen nicht gezeichnet werden, da sie ohnehin nicht sichtbar sind. Damit nicht für sämtliche Polygone einer Szene einzeln geprüft werden muss, ob sie sich innerhalb des Sichtfeldes befinden, werden nach Möglichkeit gleich ganze Objekte ausgefiltert. Sind die Objekte einfache geometrische Figuren wie etwa Quader oder Kugeln, ist der Test auch schnell gemacht (die mathematischen Details erspare ich den Lesern an dieser Stelle einmal). Um aber auch für komplexe Objekte schnell prüfen zu können, ob sie innerhalb des Frustums liegen, wird ein weiteres Verfahren, die Verwendung sog. Hüllobjekte oder Bounding Volumes, eingesetzt. Ein Bounding Volume ist eine einfache geometrische Figur (meist ein Quader oder eine Kugel), deren Ausmaße und Ausrichtung so gewählt wird, dass sie das zu untersuchende Objekt möglichst eng umschließt. Am Beispiel der weit verbreiteten Utah-Teekanne sieht ein Hüllobjekt (in diesem Fall eine Bounding Box) folgendermaßen aus:
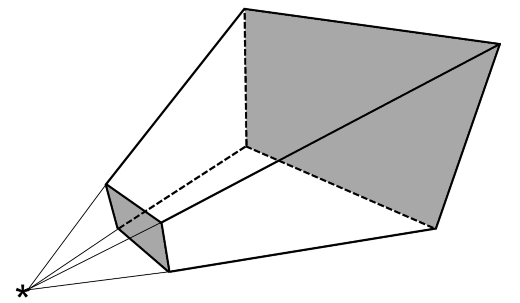
Diese geometrische Repräsentation des Objektes kann nun einfach gegen das Frustum geprüft werden; liegt das Hüllobjekt komplett außerhalb oder innerhalb des Sichtfeldes, gilt dies auch für das eigentliche Objekt. Ein Sonderfall tritt ein, wenn ein Objekt auf einer der Kanten des Frustums liegt, also nur teilweise sichtbar ist. Dieser Fall kann auf drei Arten berücksichtigt werden; entweder wird ein derartiges Objekt als “außerhalb” klassifiziert und verworfen – was aber zu dem unschönen Effekt führt, dass Objekte am Rand des Sichtfeldes plötzlich auftauchen und verschwinden (diese Art der Behandlung ist heutzutage nicht mehr üblich, kann aber teilweise bei einigen Spielen der frühen 3D-Ära beobachtet werden). Alternativ kann ein derartiges Objekt auch als “sichtbar” eingestuft und komplett gezeichnet werden, wobei die überstehenden Dreiecke zwar berechnet, die Farbinformationen durch die Grafikkarte aber verworfen werden; bei kleinen Objekten ist das auch kein Problem, bei sehr großen Objekten führt das aber dazu, dass sehr viele Dreiecke umsonst bearbeitet werden müssen. Aus diesem Grund wird heutzutage in der Regel Methode 3 angewandt: hierbei wird bestimmt, welche Polygone des Objektes innerhalb und welche außerhalb des Frustums liegen; die außerhalb liegenden werden verworfen, die innerhalb liegenden gezeichnet (wobei Dreiecke, die eine der Frustum-Ebenen schneiden, ebenso wiederum verworfen, immer gezeichnet oder beschnitten werden können). Dieser Vorgang wird als Clipping bezeichnet, daher auch die Bezeichnungen Near Clipping Plane und Far Clipping Plane. Schauen wir von oben auf eine (aus Sicht der Kamera) zu zeichnende Szene, so könnte sich etwa das folgende Bild ergeben (oben die Szene vor dem Clipping, unten danach; nur die übrigbleibenden farbigen Teile werden gezeichnet):
Durch das Frustum Culling und Clipping wurde die Anzahl der zu zeichnenden Polygone schon massiv reduziert; dennoch reicht das nicht, um selbst auf moderner Hardware Szenen mit einem hohen Detaillierungsgrad zu zeichnen; wir brauchen also Verfahren, um noch mehr Dreiecke zu zeichnen.
Eine Beobachtung aus der realen Welt hilft hier, weitere Polygone auszufiltern: normalerweise sieht man von Objekten nur die Vorderseiten; die Rückseiten sind nicht sichtbar (abgesehen von transparenten Objekten; die lassen wir hier einmal außen vor). Da ein Mesh, also eine Sammlung von Polygonen, in der Regel ein geschlossenes Objekt ist (das heißt, jedes Dreieck an allen drei Kanten ein weiteres Dreieck berührt), wissen wir, dass auch in der Szene die Dreiecke der Rückseite eines Objektes niemals sichtbar sind (mit Rückseite ist die vom Betrachter abgewandte Seite eines Objektes gemeint). Wenn wir diese ausfiltern könnten, hätten wir wieder eine große Menge an Polygonen zum Zeichnen (im Schnitt wohl die Hälfte) eingespart.
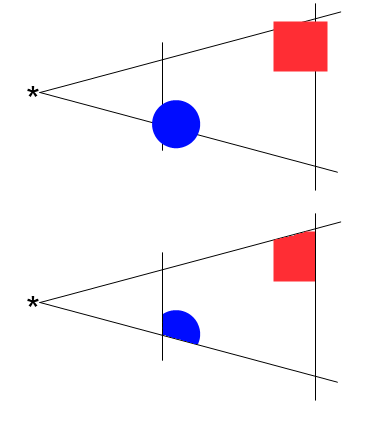
An dieser Stelle greift das Verfahren des Backface Culling. Wie es der Name schon andeutet, werden hierbei sämtliche Dreiecke entfernt, die auf der Rückseite eines Objektes liegen. Ein einfacher mathematischer Kniff hilft, diese Polygone zu identifizieren. Jedes Dreieck besitzt einen Normalenvektor, also einen Vektor, der genau senkrecht zur Dreiecksfläche orientiert ist und, entsprechend der Konvention, in die gleiche Richtung wie die Vorderseite zeigt (der Normalenvektor lässt sich übrigens durch die Reihenfolge der Dreieckspunkte bestimmen, da die drei Punkte eines Polygons reichen, um den Normalenvektor zu beschreiben). Zusätzlich ist ja die Blickrichtung des Betrachters, ebenfalls ein Vektor, bekannt. Nun der Kniff: zeigen Normalenvektor und Blickrichtung grob in die gleiche Richtung (sprich, ist der Winkel zwischen den beiden Vektoren nicht größer als 90°), so schauen wir auf die Rückseite des entsprechenden Dreiecks und es kann verworfen werden; ist der Winkel zwischen Dreiecksnormale und Blickrichtung dagegen größer als 90°, sehen wir die Vorderseite. Es muss also nur für jedes Dreieck bestimmt werden, wohin sein Normalenvektor zeigt, damit bestimmt werden kann, ob es relevant ist oder nicht (wer an den mathematischen Details des Verfahrens interessiert ist, kann sie hier nachlesen). Von oben betrachtet könnte das so aussehen (die dickeren Striche repräsentieren von oben gesehene Dreiecke, die beiden grünen sind sichtbar, die beiden roten nicht):


Kommentare (2)