Künstliche neuronale Netze: Intelligenz im Computer – Teil 2

Die drei Neuronen lassen sich übrigens grafisch folgendermaßen darstellen (Reihenfolge: NICHT, ODER, UND):

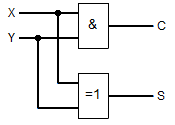
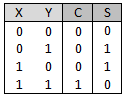
Durch Verknüpfung mehrerer Neuronen können nun alle möglichen logischen Schaltungen nachgebaut werden. Eine sehr einfache (uns schon bekannte) ist die Schaltung zur Addition zweier einzelner Bits, die ja bekanntlich mit Hilfe eines UND- und eines XOR-Gatters realisiert werden kann. Die logische Schaltung und die Schalttabelle für diese einfache Schaltung sahen so aus:

Wie zu sehen, benötigen wir für die Schaltung ein XOR-Gatter (⨁). Die XOR-Funktion lässt sich aber ganz einfach mit Hilfe von NICHT (¬), UND
(∧) und ODER (∨) ausdrücken:

X ⨁ Y = ( X ∧ ¬Y ) ∨
( ¬X ∧
Y )

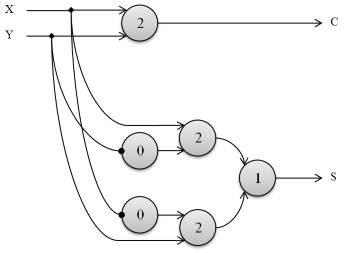
Als künstliches neuronales Netz sieht die gesamte Schaltung also folgendermaßen aus (das XOR bläht sie ein wenig auf; zur Übersichtlichkeit wurden die Gewichte weggelassen und negative Gewichte mit einem kleinen Kreis markiert):

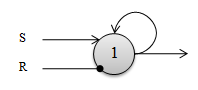
Jetzt fehlt zur Simulation eines kompletten Computers eigentlich nur noch eine Möglichkeit, Informationen auch dauerhaft speichern zu können. Auch das lässt sich mit künstlichen Neuronen überaus elegant lösen, funktioniert allerdings anders als in einem echten Gehirn. In letzterem werden die Informationen hauptsächlich durch die Vernetzung zwischen den Neuronen gespeichert; in unserem künstlichen neuronalen Netz wollen wir die Informationen in den Neuronen hinterlegen. Dazu wird sich einer einfachen Technik bedient, nämlich der Weiterleitung der Ausgabe eines Neurons auf seine eigene Eingabe. Betrachten wir das folgende einfache künstliche Neuron (alle Gewichte sind wieder 1 beim Pfeil und -1 beim kleinen Kreis):

Neben den beiden offenkundigen Eingängen S (Set) und R (Reset) hat das Neuron noch einen dritten (namenlosen) Eingang, wobei der Ausgabewert des Neurons direkt auf diesen Eingang geleitet wird. Solange an den beiden Eingängen S und R jeweils kein Wert anliegt, erhält sich der Ausgabewert des Neurons selber (bei einer 0 als Ausgabe wird der Schwellwert nicht erreicht und die Ausgabe bleibt 0, bei einer 1 als Ausgabe wird der Schwellwert gerade erreicht und die Ausgabe bleibt 1) – das Neuron speichert also ein einzelnes Bit. Durch ein kurzes Signal am S-Eingang kann eine Information in das Neuron geschrieben werden (da hierdurch der Schwellwert erreicht wird, das Neuron feuert und sich die Information in Folge selbst erhält), durch ein Signal am R-Eingang wird die gespeicherte Information zurückgesetzt (durch das negative Gewicht ergibt sich in Summe aller Eingänge ein Wert von kleiner oder gleich 0, was unterhalb des Schwellwertes liegt – das Neuron feuert damit nicht mehr). Werden auf beide Eingänge S und R gleichzeitig ein Signal gegeben, ändert sich übrigens nichts am gespeicherten Wert.

Das künstliche Neuron fungiert somit als einfacher Speicher, der eine Information von einem Bit dauerhaft speichern kann; durch eine geeignete Aneinanderreihung mehrerer derartiger Neuronen kann unser neuronales Netz nun also auch Informationen speichern. Zusammen mit den Neuronen für die logischen Operationen könnte nun also ein beliebiger Computer nachgebildet werden. Einen großen Sinn hat das natürlich nicht, da es ja Computer schon gibt und es nicht allzu viel bringt, sie durch ein künstliches Netz nachzubauen; es verdeutlicht aber doch relativ gut, wie derartige Netze künstliche Neuronen im Prinzip funktionieren. Bei der konkreten Anwendung wird allerdings ein wenig anders vorgegangen, aber dazu gibt es im nächsten Artikel ein paar mehr Informationen.