Künstliche neuronale Netze: Intelligenz im Computer – Teil 2

Im ersten Teil der Serie zu den künstlichen neuronalen Netzen wurden die Grundlagen der Informationsverarbeitung im Gehirn, die Funktionsweise eines Neurons und das elektronische Äquivalent dazu – das künstliche Neuron – erklärt. Heute wollen wir sehen, wie mit Hilfe der künstlichen Neuronen ebenfalls eine Informationsverarbeitung realisiert werden kann.

Zuerst einmal (und mehr oder weniger unabhängig von dem, was noch folgt) wollen wir aber zeigen, dass ein künstliches neuronales Netz ebenso mächtig ist wie ein beliebiger moderner Computer, das heißt, die gleichen Dinge berechnen kann. Dazu ist es nötig zu wissen, wie Computer grundsätzlich überhaupt arbeiten, das heißt, wie sie einen Strom von Informationen verarbeiten können. Alte Hasen können jetzt einfach weiterlesen, allen anderen empfehle ich meine Artikelserie zum Thema “Wie Rechner rechnen“.

Die Basis der Informationsverarbeitung im Computer stellen die logischen Operationen dar, allen voran die Basisverknüpfungen UND, ODER und NICHT. Mit Ihrer Hilfe lässt sich jede beliebige Verknüpfung von binären Zahlen darstellen; ein System, welches diese Operationen beherrscht und über einen Speicher verfügt, ist –  was die Rechenfähigkeit angeht – ebenso mächtig wie ein handelsüblicher Computer. Ein KNN könnte nun genau dafür benutzt werden; in der Praxis hat das zwar keinen großen Nutzen (immerhin haben wir ja normale Computer), ist aber dennoch interessant, weswegen ich es auch im Folgenden vorstellen möchte. Also immer im Hinterkopf behalten: für die tatsächliche Anwendung künstlicher neuronaler Netze spielt dieser Artikel nur eine untergeordnete Rolle; zum Verständnis der Funktionsweise ist er aber geeignet.

Noch eine Anmerkung, bevor es losgeht: wenn ich im weiteren Verlauf von “Neuronen” rede, so sind damit in der Regel “künstliche Neuronen” gemeint.

Als erstes wollen wir die drei oben genannten Basisverknüpfungen UND, ODER und NICHT mit Hilfe künstlicher Neuronen darstellen. Zur Erinnerung hier noch einmal die Verknüpfungstabelle (in der Reihenfolge NICHT, UND, ODER):

Aus dem letzten Teil wissen wir, dass jedes künstliche Neuron über eine Menge von gewichteten Eingabekanälen, einem Schwellwert, einer Aktivierungsfunktion und natürlich dem Ausgabekanal besteht. Zur Realisierung der NICHT-Funktion wird daher ein Neuron mit einer Eingabe und für die UND- und ODER-Funktion jeweils ein Neuron mit 2 Eingaben benötigt. Für alle drei Neuronen soll gelten, dass sie als Aktivierungsfunktion eine einfache Sprungfunktion verwenden, die beim Überschreiten eines bestimmten Schwellwertes den Wert 1, ansonsten den Wert 0 erzeugt.

Die Neuronen für die UND- und ODER-Funktion lassen sich somit auch ganz einfach beschreiben; die Eingabegewichte werden dazu für alle Eingaben auf den Wert 1 gesetzt und als Schwellwert für das UND-Neuron der Wert 2 und für das ODER-Neuron der Wert 1 gewählt. Wenn wir kurz nachrechnen, erschließt sich dieses Vorgehen auch sofort:

Zur Berechnung des Ausgabewertes eines künstlichen Neurons werden alle Eingaben mit ihrem Gewicht multipliziert, aufaddiert und als Argument für die Aktivierungsfunktion verwendet; erreicht oder überschreitet der Wert des Arguments den Schwellwert, so wird bei einer Sprungfunktion der höhere Wert (hier: 1), ansonsten der niedrigere (hier: 0) erzeugt (und ja, eine Sprungfunktion kann auch umgekehrt funktionieren).

Für unser ODER-Neuron bedeutet das, dass der Schwellwert 1 erreicht wird, sobald mindestens eine der beiden Eingaben den Wert 1 aufweist (da das Gewicht ebenfalls 1 ist, hat es keine weitere Auswirkung). Das Neuron feuert also, wenn wenigstens eine der Eingaben 1 ist, womit es genau der ODER-Funktion entspricht. Analog dazu feuert das UND-Neuron erst, wenn an beiden Eingabekanälen der Wert 1 anlegt, da nur so der Schwellwert von 2 erreicht wird.

Das NICHT-Neuron wird nun nach dem gleichen Gedankengang umgesetzt; allerdings benötigen wir hier als Gewicht für die einzige Eingabe den Wert -1 und nutzen als Schwellwert 0. Die Überlegung dahinter ist einfach: erhält das Neuron eine 1 als Eingabewert, so wird diese mit dem Gewicht von -1 multipliziert; das Ergebnis (ebenfalls -1) ist natürlich kleiner als 0, wodurch das Neuron nicht feuert. Bei einer Eingabe von 0 allerdings wird der Wert von 0 in die Aktivierungsfunktion gegeben, wodurch gerade der Schwellwert erreicht wird und das Neuron feuert.

Die drei Neuronen lassen sich übrigens grafisch folgendermaßen darstellen (Reihenfolge: NICHT, ODER, UND):

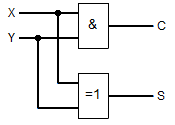
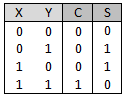
Durch Verknüpfung mehrerer Neuronen können nun alle möglichen logischen Schaltungen nachgebaut werden. Eine sehr einfache (uns schon bekannte) ist die Schaltung zur Addition zweier einzelner Bits, die ja bekanntlich mit Hilfe eines UND- und eines XOR-Gatters realisiert werden kann. Die logische Schaltung und die Schalttabelle für diese einfache Schaltung sahen so aus:

Wie zu sehen, benötigen wir für die Schaltung ein XOR-Gatter (⨁). Die XOR-Funktion lässt sich aber ganz einfach mit Hilfe von NICHT (¬), UND
(∧) und ODER (∨) ausdrücken:

X ⨁ Y = ( X ∧ ¬Y ) ∨
( ¬X ∧
Y )

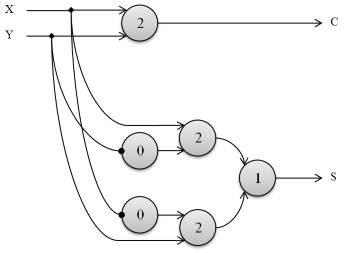
Als künstliches neuronales Netz sieht die gesamte Schaltung also folgendermaßen aus (das XOR bläht sie ein wenig auf; zur Übersichtlichkeit wurden die Gewichte weggelassen und negative Gewichte mit einem kleinen Kreis markiert):

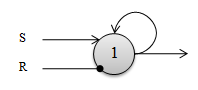
Jetzt fehlt zur Simulation eines kompletten Computers eigentlich nur noch eine Möglichkeit, Informationen auch dauerhaft speichern zu können. Auch das lässt sich mit künstlichen Neuronen überaus elegant lösen, funktioniert allerdings anders als in einem echten Gehirn. In letzterem werden die Informationen hauptsächlich durch die Vernetzung zwischen den Neuronen gespeichert; in unserem künstlichen neuronalen Netz wollen wir die Informationen in den Neuronen hinterlegen. Dazu wird sich einer einfachen Technik bedient, nämlich der Weiterleitung der Ausgabe eines Neurons auf seine eigene Eingabe. Betrachten wir das folgende einfache künstliche Neuron (alle Gewichte sind wieder 1 beim Pfeil und -1 beim kleinen Kreis):

Neben den beiden offenkundigen Eingängen S (Set) und R (Reset) hat das Neuron noch einen dritten (namenlosen) Eingang, wobei der Ausgabewert des Neurons direkt auf diesen Eingang geleitet wird. Solange an den beiden Eingängen S und R jeweils kein Wert anliegt, erhält sich der Ausgabewert des Neurons selber (bei einer 0 als Ausgabe wird der Schwellwert nicht erreicht und die Ausgabe bleibt 0, bei einer 1 als Ausgabe wird der Schwellwert gerade erreicht und die Ausgabe bleibt 1) – das Neuron speichert also ein einzelnes Bit. Durch ein kurzes Signal am S-Eingang kann eine Information in das Neuron geschrieben werden (da hierdurch der Schwellwert erreicht wird, das Neuron feuert und sich die Information in Folge selbst erhält), durch ein Signal am R-Eingang wird die gespeicherte Information zurückgesetzt (durch das negative Gewicht ergibt sich in Summe aller Eingänge ein Wert von kleiner oder gleich 0, was unterhalb des Schwellwertes liegt – das Neuron feuert damit nicht mehr). Werden auf beide Eingänge S und R gleichzeitig ein Signal gegeben, ändert sich übrigens nichts am gespeicherten Wert.

Das künstliche Neuron fungiert somit als einfacher Speicher, der eine Information von einem Bit dauerhaft speichern kann; durch eine geeignete Aneinanderreihung mehrerer derartiger Neuronen kann unser neuronales Netz nun also auch Informationen speichern. Zusammen mit den Neuronen für die logischen Operationen könnte nun also ein beliebiger Computer nachgebildet werden. Einen großen Sinn hat das natürlich nicht, da es ja Computer schon gibt und es nicht allzu viel bringt, sie durch ein künstliches Netz nachzubauen; es verdeutlicht aber doch relativ gut, wie derartige Netze künstliche Neuronen im Prinzip funktionieren. Bei der konkreten Anwendung wird allerdings ein wenig anders vorgegangen, aber dazu gibt es im nächsten Artikel ein paar mehr Informationen.