Haben wir nun so die Kontur bestimmt, muss diese gefüllt werden. Das Vorgehen hierfür drängt sich schon beinahe auf: Ausgehend vom ersten eingefärbten Pixel einer Zeile müssen lediglich alle weiteren eingefärbt werden, bis das bereits eingefärbte Pixel erreicht wird. Das lässt sich auch wunderbar als Pseudocode (also informale Beschreibung eines Algorithmus) notieren; nehmen wir an, wir kennen durch das Zeichnen der Kontur die Punkte xmin, xmax, ymin und ymax, die jeweils die kleinsten und größten x- und y-Werte der eingefärbten Pixel (sprich, die x- und y-Werte der am weitesten links/rechts/oben/unten liegenden Pixel) enthalten; dann lässt sich der Algorithmus zum Beispiel folgendermaßen aufschreiben (es sind natürlich auch andere Umsetzungen denkbar):
(2) for each y from ymin to ymax:
(3) for each x1 from xmin to xmax:
(4) if pixel(x1,y) filled:
(5) for each x2 from x1+1 to xmax:
(6) if pixel(x2,y) filled: continue at (2)
(7) else: fill pixel(x2,y)
Eigentlich ganz einfach, oder? Diesen Algorithmus können wir nun auf obige Kontur loslassen, was uns zu folgendem wenig überraschendem Bild führt:
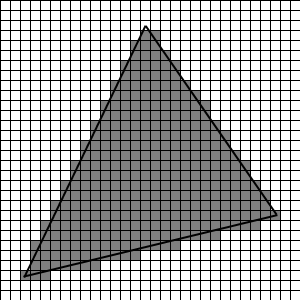
Manchmal kann es übrigens passieren, dass 2 Konturpixel verschiedener Kanten auf den gleichen Bildpunkt entfallen, und zwar in der Regel in der nähe der Eckpunkte des Dreiecks; so ein Fall benötigt eine gesonderte Behandlung, etwa, indem derartige Punkte nicht mit in die Kontur aufgenommen werden.
Damit haben wir nun endlich eine Möglichkeit, um gefüllte Dreiecksflächen darstellen zu können – ein wichtiger Schritt auf dem Weg zur Darstellung komplexer Objekte. Prinzipiell reicht das zwar schon, aber es fehlt natürlich noch eine ganz wichtige Information: nämlich die Farbgebung der Dreiecke. Dazu gibt es dann aber im nächsten Artikel etwas.
Vorher möchte ich aber noch auf einen Leserwunsch eingehen, nämlich zum Thema indizierte Dreieckslisten. Wie im letzten Artikel angedeutet, werden komplexe Objekte zwar aus einzelnen Dreiecken aufgebaut, jedoch werden diese Dreiecke nicht alle separat gespeichert. Das wäre ein sinnloser Aufwand an Speicherplatz, da sich die meisten Dreiecke ein oder zwei Eckpunkte Teilen würden. Aus diesem Zweck wird zur Abspeicherung der zu einem Objekt gehörenden Dreiecke eine spezielle Struktur verwendet, die sogenannte indizierte Dreiecksliste.
Der Name ist allerdings etwas irreführend – tatsächlich handelt es sich nämlich nicht um eine, sondern um zwei Listen. Aber eins nach dem anderen. Schauen wir uns zuerst die herkömmliche Art der Speicherung an, mit 3 Punkten für jedes Dreieck. Untenstehend ist ein Bild mit 3 Dreiecken zu sehen; hierfür müssen insgesamt 9 Eckpunkte gespeichert werden (man möge mir die etwas unschöne Art der Darstellung verzeihen):
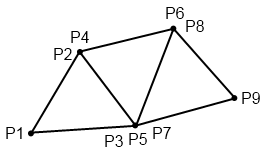
Es ist zu sehen, dass zwei der Punkte von jeweils 2, ein Punkt sogar von allen drei Dreiecken geteilt wird – das jeweils erneute Abspeichern der Punkte ist im Grunde also Platzverschwendung. Um hier zu sparen, wurde (neben anderen Methoden der Speicherung) das Verfahren der indizierten Dreiecksliste entwickelt. Bei diesem Verfahren werden zunächst einmal tatsächlich nur alle Punkte (das heißt, für jeden Punkt der x-, y- und z-Wert) genau einmal in einer Liste, der Dreiecksliste, abgespeichert – für obiges Beispiel also die folgenden Punkte:
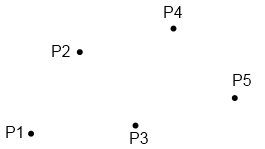
Die Liste (mit fiktiven Werten) für die obigen 5 Punkte könnte also so aussehen (die z-Werte sind in der Abbildung natürlich nicht zu erkennen):
- P1: (90, 130, 10)
- P2: (80, 50, 13)
- P3: (135, 125, 8)
- P4: (175, 30, 14)
- P5: (235, 95, 5)
Um aus diesen Punkten nun Dreiecke generieren zu können, wird zusätzlich eine weitere Liste, die Indexliste, angelegt, welche für jedes Dreieck die Position der zum Dreieck gehörenden Punkte in der Dreiecksliste – den sogenannten Index – enthält. Da jedes Dreieck immer aus genau 3 Punkten besteht, werden in der Indexliste pro Dreieck immer 3 Indizes abgespeichert – für alle Dreiecke einfach hintereinander, da ja die Anzahl der Punkte pro Dreieck bekannt ist. Für obiges Beispiel ergibt sich also die folgende Indexliste (im Gegensatz zur gängigen Informatikpraxis als 1-indizierte und nicht als 0-indizierte Liste):
1, 2, 3, 2, 4, 3, 3, 4, 5
Die Indexliste besagt, dass das erste Dreieck aus den Punkte 1, 2, 3; das zweite aus den Punkten 2, 4, 3 und das dritte aus den Punkten 3, 4, 5 besteht.1 Statt der vormals benötigten 9 Punkte reichen nun also 5 Punkte aus – dafür muss aber natürlich noch die Indexliste gespeichert werden.

Kommentare (3)