Computergrafik – Teil 4

Im letzten Artikel haben wir besprochen, wie sich aus einzelnen Punktinformationen Dreiecke auf den Bildschirm zaubern lassen. Viel gekonnt haben wir damit allerdings nicht, da wir lediglich die Umrisse der Dreiecke zeichnen konnten. Was aber eigentlich benötigt ist, sind komplett ausgefüllte Dreiecke – und darum soll es heute gehen.

Ebenso wie beim Rastern von Linien gibt es natürlich auch beim Ausfüllen von Dreiecken die verschiedensten Methoden, um zum Ziel zu gelangen, wobei ich mich wie immer auf eine der einfacheren beschränke. Zu sagen ist noch, dass die beschriebene Methode natürlich nicht nur für Dreiecke funktioniert – für diese ist sie jedoch mit dem geringsten Rechenaufwand umsetzbar, weswegen das Dreieck auch (wie bereits erwähnt) die Grundlage der 3D-Grafik bildet.

Ausgangspunkt beim Rendern von Dreiecken sind wieder die in Bildschirmkoordinaten transformierten Eckpunkte des Dreiecks (wir erinnern uns). doch statt den Umriss des Dreiecks zu zeichnen, also die drei Eckpunkte durch Linien zu verbinden, wollen wir diesmal die durch die Eckpunkte beschriebene Fläche auf dem Bildschirm füllen.

Der triviale Ansatz zum Füllen des Dreiecks wäre nun natürlich, für jeden Bildschirm-Punkt zu bestimmen, ob er innerhalb oder außerhalb des Dreiecks liegt; das lässt sich durch drei relativ einfache Berechnungen bestimmen (indem nämlich geschaut wird, ob der zu betrachtende Punkt für alle drei Dreieckskanten auf der gleichen Seite liegt – ist dem so, liegt der Punkt auch im Dreieck). Aber dieser Ansatz ist uns a) zu einfach und b) ist er natürlich auch viel zu langsam, um in der Praxis relevant zu sein.

Wir wollen uns an dieser Stelle daher einen weitaus eleganteren Algorithmus anschauen, der (natürlich modifiziert) so auch in der Praxis zur Anwendung kommt. Da Algorithmen zum Zeichnen
von Dreiecken sehr schnell arbeiten müssen, sind sie meist relativ einfach gestrickt – so auch dieser. Die Rede ist vom sogenannten Edge-Flag-Algorithmus (eine für allgemeine Polygone geeignete Beschreibung findet sich hier – die Dreiecksvariante ist ein klein wenig einfacher). Das schöne ist, dass dieser Algorithmus wenigstens teilweise auch mit der Umrandung des Dreiecks arbeitet – unsere Bemühungen im vorherigen Artikel waren also nicht ganz umsonst.

Der Algorithmus besteht im Grunde aus 2 Schritten. Im ersten Schritt wird die Kontur des Dreiecks markiert; im zweiten Schritt werden dann die Pixel innerhalb der Kontur gefüllt.

Die Kontur ist so etwas ähnliches wie der Umriss des Dreiecks, mit einer kleinen Abweichung. Beim Umriss des Dreiecks haben wir unterschieden, ob eine Linie einen Anstieg von größer als 0.5 (oder kleiner als -0.5) hat – wenn dem so war, würde für jeden y-Wert der Linie ein passender x-Wert berechnet, ansonsten andersherum (wer sich nicht mehr erinnert, möge noch einmal den letzten Artikel lesen). Für die Kontur wird für alle Dreieckskanten, unabhängig von ihrem Anstieg, für alle möglichen y-Werte der Kante genau ein passender x-Wert, nämlich der am weitesten links liegende, berechnet – der sogenannte Konturpixel (x und y sowie links und rechts können beliebig ausgetauscht werden, mit entsprechender Anpassung des Algorithmus – wir halten uns hier aber an die Konvention).

Die Kontur eines Dreiecks lässt sich relativ leicht berechnen; dazu wird lediglich für jede einzelne der drei Linien des Dreiecks für jede Pixelzeile der Schnittpunkt der Linie mit der Zeile berechnet und der entsprechende Bildpunkt eingefärbt. Dazu ein kleines Beispiel; nehmen wir das folgende zu zeichnende Dreiecke mit der zugehörigen, bereits eingezeichneten Kontur an:

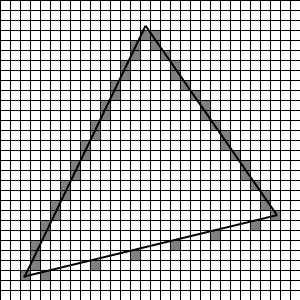
Der Unterschied der Kontur zum Umriss ist hier deutlich zu sehen, da für letzteren die untere Linie des Dreiecks einen y-Wert für jeden möglichen x-Wert aufweisen müsste. So aber wurden für alle 3 Linien für alle y-Werte mögliche x-Werte berechnet. Es fällt auf, dass sich durch dieses Vorgehen in jeder Zeile genau 2 eingefärbte Pixel befinden (das muss nicht immer so sein, dazu aber später noch ein Wort) – eine Eigenheit, die sich durch die Verwendung von Dreiecken erklären lässt.

Haben wir nun so die Kontur bestimmt, muss diese gefüllt werden. Das Vorgehen hierfür drängt sich schon beinahe auf: Ausgehend vom ersten eingefärbten Pixel einer Zeile müssen lediglich alle weiteren eingefärbt werden, bis das bereits eingefärbte Pixel erreicht wird. Das lässt sich auch wunderbar als Pseudocode (also informale Beschreibung eines Algorithmus) notieren; nehmen wir an, wir kennen durch das Zeichnen der Kontur die Punkte x_min, x_max, y_min und y_max, die jeweils die kleinsten und größten x- und y-Werte der eingefärbten Pixel (sprich, die x- und y-Werte der am weitesten links/rechts/oben/unten liegenden Pixel) enthalten; dann lässt sich der Algorithmus zum Beispiel folgendermaßen aufschreiben (es sind natürlich auch andere Umsetzungen denkbar):

Eigentlich ganz einfach, oder? Diesen Algorithmus können wir nun auf obige Kontur loslassen, was uns zu folgendem wenig überraschendem Bild führt:

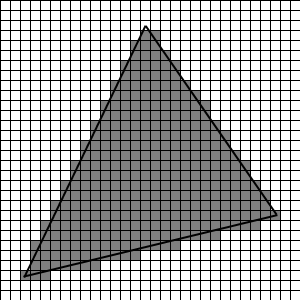
Manchmal kann es übrigens passieren, dass 2 Konturpixel verschiedener Kanten auf den gleichen Bildpunkt entfallen, und zwar in der Regel in der nähe der Eckpunkte des Dreiecks; so ein Fall benötigt eine gesonderte Behandlung, etwa, indem derartige Punkte nicht mit in die Kontur aufgenommen werden.

Damit haben wir nun endlich eine Möglichkeit, um gefüllte Dreiecksflächen darstellen zu können – ein wichtiger Schritt auf dem Weg zur Darstellung komplexer Objekte. Prinzipiell reicht das zwar schon, aber es fehlt natürlich noch eine ganz wichtige Information: nämlich die Farbgebung der Dreiecke. Dazu gibt es dann aber im nächsten Artikel etwas.

Vorher möchte ich aber noch auf einen Leserwunsch eingehen, nämlich zum Thema indizierte Dreieckslisten. Wie im letzten Artikel angedeutet, werden komplexe Objekte zwar aus einzelnen Dreiecken aufgebaut, jedoch werden diese Dreiecke nicht alle separat gespeichert. Das wäre ein sinnloser Aufwand an Speicherplatz, da sich die meisten Dreiecke ein oder zwei Eckpunkte Teilen würden. Aus diesem Zweck wird zur Abspeicherung der zu einem Objekt gehörenden Dreiecke eine spezielle Struktur verwendet, die sogenannte indizierte Dreiecksliste.

Der Name ist allerdings etwas irreführend – tatsächlich handelt es sich nämlich nicht um eine, sondern um zwei Listen. Aber eins nach dem anderen. Schauen wir uns zuerst die herkömmliche Art der Speicherung an, mit 3 Punkten für jedes Dreieck. Untenstehend ist ein Bild mit 3 Dreiecken zu sehen; hierfür müssen insgesamt 9 Eckpunkte gespeichert werden (man möge mir die etwas unschöne Art der Darstellung verzeihen):

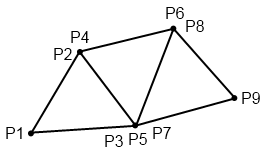
Es ist zu sehen, dass zwei der Punkte von jeweils 2, ein Punkt sogar von allen drei Dreiecken geteilt wird – das jeweils erneute Abspeichern der Punkte ist im Grunde also Platzverschwendung. Um hier zu sparen, wurde (neben anderen Methoden der Speicherung) das Verfahren der indizierten Dreiecksliste entwickelt. Bei diesem Verfahren werden zunächst einmal tatsächlich nur alle Punkte (das heißt, für jeden Punkt der x-, y- und z-Wert) genau einmal in einer Liste, der Dreiecksliste, abgespeichert – für obiges Beispiel also die folgenden Punkte:

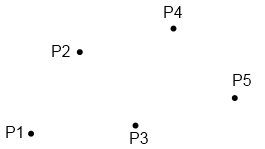
Die Liste (mit fiktiven Werten) für die obigen 5 Punkte könnte also so aussehen (die z-Werte sind in der Abbildung natürlich nicht zu erkennen):

• P1: (90, 130, 10)
• P2: (80, 50, 13)
• P3: (135, 125, 8)
• P4: (175, 30, 14)
• P5: (235, 95, 5)

Um aus diesen Punkten nun Dreiecke generieren zu können, wird zusätzlich eine weitere Liste, die Indexliste, angelegt, welche für jedes Dreieck die Position der zum Dreieck gehörenden Punkte in der Dreiecksliste – den sogenannten Index – enthält. Da jedes Dreieck immer aus genau 3 Punkten besteht, werden in der Indexliste pro Dreieck immer 3 Indizes abgespeichert – für alle Dreiecke einfach hintereinander, da ja die Anzahl der Punkte pro Dreieck bekannt ist. Für obiges Beispiel ergibt sich also die folgende Indexliste (im Gegensatz zur gängigen Informatikpraxis als 1-indizierte und nicht als 0-indizierte Liste):

1, 2, 3, 2, 4, 3, 3, 4, 5

Die Indexliste besagt, dass das erste Dreieck aus den Punkte 1, 2, 3; das zweite aus den Punkten 2, 4, 3 und das dritte aus den Punkten 3, 4, 5 besteht.¹ Statt der vormals benötigten 9 Punkte reichen nun also 5 Punkte aus – dafür muss aber natürlich noch die Indexliste gespeichert werden.

Nun könnte man argumentieren, dass man da kein gutes Geschäft macht – rechnen wir also einmal nach. Pro Dreieck werden im 3D-Raum mindestens 3 Werte benötigt, nämlich die Koordinaten (also der x-, y- und z-Wert). Üblicherweise werden pro Wert 4 Byte veranschlagt, was also 12 Byte Speicherplatz pro Punkt bedeutet. Für 9 Punkte benötigen wir also 9*12 = 108 Byte an Speicher. Für die 5 Punkte der indizierten Dreiecksliste benötigen wir lediglich 5*12 = 60 Byte an Speicherplatz; hinzu kommen die Indexwerte mit jeweils 4 Byte pro Wert (da ja eine einzelne Zahl reicht), also noch einmal 9*4 = 36 Byte, macht insgesamt 96 Byte – ein Gewinn von immerhin 12 Byte Speicherplatz (11%).

Da Objekte aber in der Regel nicht nur aus drei, sondern aus tausenden von Dreiecken bestehen, ergibt sich hier eine erkleckliche Speicherplatzersparnis. Je mehr Dreiecke sich Punkte teilen, desto
größer ist auch die Ersparnis (weswegen auch kein genereller prozentualer Wert für die Einsparung angegeben werden kann). Um eine Vorstellung von der Entwicklung der Ersparnis zu geben: nehmen wir im obigen Beispiel (dem ganz oben, mit den doppelt gespeicherten Punkten) noch einen weiteren Punkt P10 hinzu, welcher mit den Punkten P4 und P6 ein weiteres Dreieck bildet, so lassen sich mit Hilfe der indizierten Dreiecksliste bereits 24 Byte, also ungefähr 17% Speicherplatz sparen. Alles in allem sollte das genügend Motivation für die Verwendung von indizierten Dreieckslisten sein.

^{1 Wer sich jetzt über die Reihenfolge der Indizes für das zweite Dreieck wundert: es ist von Vorteil, die Indizes so zu sortieren, dass die Punkte aller Dreiecke im gleichen Drehsinn (hier: im Uhrzeigersinn) gespeichert werden, wenn “von vorne” auf das Dreieck geschaut wird. Der Grund ist, dass sich dadurch unter anderem Sichtbarkeitstests einfach durchführen lassen – dazu aber später bei Wunsch noch ein paar Worte.}