Die Nachteile dieser Methode liegen auf der Hand: zum einen würde man so für jedes Dreieck ein eigenes Bild benötigt, von dem dann auch noch immer nur die Hälfte ausnutzen kann. Das wäre natürlich eine enorme Verschwendung von Speicherplatz und gleichzeitig ein ziemlich großer Aufwand, um komplexere Objekte mit Oberflächendetails zu versehen. Das Mapping der Bilder auf die Dreiecke muss also anders erfolgen. Zu diesem Zweck bedient man sich in der Praxis der Texturkoordinaten.
Vereinfacht gesagt sind Texturkoordinaten ganz ähnlich zu den bereits bekannten dreidimensionalen Koordinaten der Eckpunkte der Dreiecke, mit dem Unterschied, dass sie keine Position in der Welt beschreiben, sondern eine Position auf der Textur; dementsprechend sind sie auch nicht dreidimensional, sondern es reichen 2 Werte, einer für die Breite und einer für die Höhe (es gibt auch dreidimensionale Texturkoordinaten, wenn etwa volumetrische oder prozedurale Texturen zum Einsatz kommen – das soll an dieser Stelle aber nicht weiter interessieren). Über die Texturkoordinaten kann also angegeben werden, auf welche Positionen in der Textur die 3 Eckpunkte eines Dreiecks projiziert werden sollen. Damit können viele Dreiecke über ein einziges Bild effektiv eingefärbt und zudem der ungenutzte Platz in einem Bild minimiert werden. Texturkoordinaten werden üblicherweise im Intervall [0,1] angegeben, wobei der Punkt (0,0) z.B. die linke obere und der Punkt (1,1) die rechte untere Ecke der Textur markiert (das ist allerdings kein festes Gesetz und kann in der Praxis auch anders definiert sein); üblicherweise werden Texturkoordinaten mit den Variablen u und v (und w, wenn es 3 davon gibt) bezeichnet, analog zu x, y und z der Positions-Koordinaten – man spricht daher auch vom UV-Mapping.
Auch hierzu ein kleines Beispiel; die folgende Abbildung zeigt die bereits bekannte Textur, auf die mehrere Dreiecke projiziert wurden, die zusammengesetzt einen Würfel ergeben würden:
Wendet man diese Projektion nun beim Zeichnen des Würfels an, so erhält man (ungefähr – das Mapping ist hier nicht ganz exakt, was aber dem Beispiel keinen Schaden tut) das folgende Bild:
Dem aufmerksamen Beobachter fällt natürlich auch hier die harte Kante in der Textur des Würfels an seinem oberen Rand auf; die ist durch die Projektion der Dreiecke auf die Textur bedingt (die Dreiecke liegen in der Textur ja nicht alle direkt nebeneinander) und es ist die Aufgabe des Modellierers (also desjenigen, der die Objekte erstellt), dafür zu sorgen, dass die Textur passend auf das Objekt projiziert wird.
Damit wissen wir nun endlich, wie man nicht nur die Geometrie auch komplexer Objekte darstellt, sondern auch, wie man die Objekte mit geeigneten Oberflächenstrukturen versieht. Damit möchte ich prinzipiell die Serie zur Computergrafik auch vorerst abschließen. Wenn allerdings noch Wünsche zu bestimmten Themen aus diesem Themenkomplex bestehen, so können die natürlich gern in den Kommentaren gepostet werden.
Ansonsten geht es das nächste mal (hoffentlich) mit einem mindestens ebenso spannenden Thema weiter. Um einen Hinweis zu geben: es wird um die Frage gehen, wie die Informatik genutzt werden kann, um wissenschaftliche Theorien zu untersuchen.

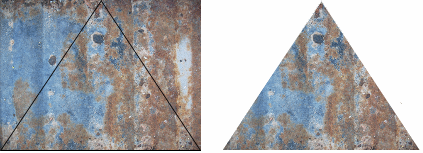


Kommentare (6)