So, nun folgt endlich der nächste Artikel zum Thema Computergrafik. Der letzte Artikel hat sich damit beschäftigt, wie mit Hilfe einfacher mathematischer Methoden ein gefülltes Dreieck auf den Bildschirm gezeichnet werden kann. Eine wichtige Sache fehlte dabei allerdings, nämlich die Einfärbung der Dreiecke zur Darstellung von Oberflächeninformationen – und darum soll es heute gehen.
Die einfachste Form der Einfärbung ist natürlich, beim Füllen der Dreiecke kein modisches Grau als Farbe zu verwenden, sondern eine beliebige andere Farbe. Viel gekonnt hat man damit allerdings nicht; aus einem Objekt mit grauen Dreiecken wird dann beispielsweise ein Objekt mit blauen Dreiecken – das ist nur in wenigen Fällen eine Verbesserung.
Hilfreicher wäre es dagegen, wenn jedes Dreieck mit einer anderen Farbe eingefärbt werden könnte. Auch das ist relativ leicht umsetzbar; hierfür wird für jedes Dreieck neben seinen 3 Eckpunkten noch die Information gespeichert, in welcher Farbe es eingefärbt werden soll. Beim Zeichnen eines Objektes muss nun lediglich die entsprechende Information beim Füllen der einzelnen Dreiecke berücksichtigt werden. Das könnte zum Beispiel im Ergebnis dann so aussehen:
Man sieht allerdings: so wirklich schön ist das nicht. Zwischen den verschiedenen Dreiecken gibt es nun harte Kanten, bedingt dadurch, dass jedes Dreieck eine einzige Farbe hat. Bei genügend großer Anzahl an Dreiecken würden diese Kanten zwar immer weniger auffallen, aber für eine ansehnliche Einfärbung (wie zum Beispiel hier zu sehen) bräuchte man eine derart große Anzahl an Dreiecken, dass selbst auf moderner Hardware keine größeren Szenen dargestellt werden könnten. Ein anderes Verfahren muss also her.
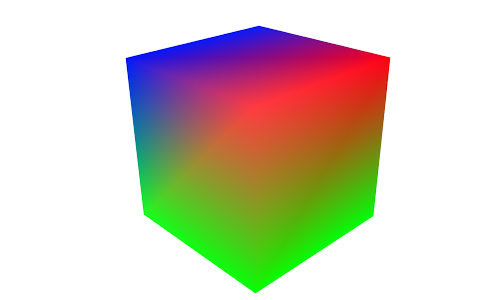
Die gängige Möglichkeit zur Einfärbung von Dreiecken ist Interpolation von Farben. Hierbei wird nicht mehr eine einzige Farbinformation pro Dreieck gespeichert, sondern für jeden Eckpunkt eine eigene Farbe definiert. Beim Füllen eines Dreiecks wird nun nicht eine einzige Farbe für das gesamte Dreieck verwendet, sondern zwischen den Farben der drei Eckpunkte interpoliert, das heißt, jeder Pixel des Dreiecks wird in Abhängigkeit zur Entfernung zu den Eckpunkten entsprechend eingefärbt. Für ein einzelnes Dreieck würde das Ergebnis also so aussehen:
Teilen sich zwei Dreiecke einen oder gemeinsame Eckpunkte (und damit auch die darin gespeicherten Farbinformationen), gibt es an den Berührungspunkten der beiden Dreiecke keine harte Farbkante mehr, sondern einen sanften Farbverlauf. Bezogen auf ein komplexeres Objekt könnte man also das folgende Bild erreicht werden:
Das sieht ja nun schon ganz brauchbar aus. Trotzdem sieht es natürlich noch nicht nach dem aus, was man an grafischer Darstellung aus gängigen 3D-Spielen gewohnt ist – es fehlen nach wie vor die Details bei der Darstellung. Zwar könnte man auch hier durch eine immense Erhöhung der Anzahl der Dreiecke mehr Oberflächendetails darstellen, aber der Rechenaufwand hierfür ist einfach zu groß (und das Ergebnis würde zweifelhaft bleiben). Es ist also nach wie vor ein besseres Verfahren zur Darstellung von Oberflächeninformationen nötig.
Die Methode der Wahl ist hier das sogenannte Texture Mapping. Bei diesem Verfahren wird ein Dreieck nicht einfach nur anhand der Eckpunkt-Farben eingefärbt, sondern es wird ein 2-dimensionales Bild – die Textur – auf das Dreieck gelegt. Dieses Bild enthält dabei benötigten Farbinformationen, um die gewünschte Oberflächenstruktur darzustellen. Zur Abbildung des Bildes auf das Dreieck – das Mapping – werden nun die drei Eckpunkte des Dreiecks auf drei Punkte im Bild projiziert und die dazwischenliegenden Farbinformationen – die Punkte des Bildes, sogenannte Texel – auf das Dreieck übertragen. Im einfachsten Fall erfolgt das Mapping immer nach einem festen Schema, bei dem zum Beispiel die linke untere Ecke des Bildes mit dem ersten Eckpunkt des Dreiecks, die rechte untere Ecke des Bildes mit dem zweiten Eckpunkt und der mittlere Punkt oben mit dem dritten Eckpunkt assoziiert wird. Das könnte dann z.B. so aussehen (links: die Textur mit darauf projiziertem Dreieck, rechts: das texturierte Dreieck):
Die Nachteile dieser Methode liegen auf der Hand: zum einen würde man so für jedes Dreieck ein eigenes Bild benötigt, von dem dann auch noch immer nur die Hälfte ausnutzen kann. Das wäre natürlich eine enorme Verschwendung von Speicherplatz und gleichzeitig ein ziemlich großer Aufwand, um komplexere Objekte mit Oberflächendetails zu versehen. Das Mapping der Bilder auf die Dreiecke muss also anders erfolgen. Zu diesem Zweck bedient man sich in der Praxis der Texturkoordinaten.
Vereinfacht gesagt sind Texturkoordinaten ganz ähnlich zu den bereits bekannten dreidimensionalen Koordinaten der Eckpunkte der Dreiecke, mit dem Unterschied, dass sie keine Position in der Welt beschreiben, sondern eine Position auf der Textur; dementsprechend sind sie auch nicht dreidimensional, sondern es reichen 2 Werte, einer für die Breite und einer für die Höhe (es gibt auch dreidimensionale Texturkoordinaten, wenn etwa volumetrische oder prozedurale Texturen zum Einsatz kommen – das soll an dieser Stelle aber nicht weiter interessieren). Über die Texturkoordinaten kann also angegeben werden, auf welche Positionen in der Textur die 3 Eckpunkte eines Dreiecks projiziert werden sollen. Damit können viele Dreiecke über ein einziges Bild effektiv eingefärbt und zudem der ungenutzte Platz in einem Bild minimiert werden. Texturkoordinaten werden üblicherweise im Intervall [0,1] angegeben, wobei der Punkt (0,0) z.B. die linke obere und der Punkt (1,1) die rechte untere Ecke der Textur markiert (das ist allerdings kein festes Gesetz und kann in der Praxis auch anders definiert sein); üblicherweise werden Texturkoordinaten mit den Variablen u und v (und w, wenn es 3 davon gibt) bezeichnet, analog zu x, y und z der Positions-Koordinaten – man spricht daher auch vom UV-Mapping.
Auch hierzu ein kleines Beispiel; die folgende Abbildung zeigt die bereits bekannte Textur, auf die mehrere Dreiecke projiziert wurden, die zusammengesetzt einen Würfel ergeben würden:
Wendet man diese Projektion nun beim Zeichnen des Würfels an, so erhält man (ungefähr – das Mapping ist hier nicht ganz exakt, was aber dem Beispiel keinen Schaden tut) das folgende Bild:
Dem aufmerksamen Beobachter fällt natürlich auch hier die harte Kante in der Textur des Würfels an seinem oberen Rand auf; die ist durch die Projektion der Dreiecke auf die Textur bedingt (die Dreiecke liegen in der Textur ja nicht alle direkt nebeneinander) und es ist die Aufgabe des Modellierers (also desjenigen, der die Objekte erstellt), dafür zu sorgen, dass die Textur passend auf das Objekt projiziert wird.
Damit wissen wir nun endlich, wie man nicht nur die Geometrie auch komplexer Objekte darstellt, sondern auch, wie man die Objekte mit geeigneten Oberflächenstrukturen versieht. Damit möchte ich prinzipiell die Serie zur Computergrafik auch vorerst abschließen. Wenn allerdings noch Wünsche zu bestimmten Themen aus diesem Themenkomplex bestehen, so können die natürlich gern in den Kommentaren gepostet werden.
Ansonsten geht es das nächste mal (hoffentlich) mit einem mindestens ebenso spannenden Thema weiter. Um einen Hinweis zu geben: es wird um die Frage gehen, wie die Informatik genutzt werden kann, um wissenschaftliche Theorien zu untersuchen.



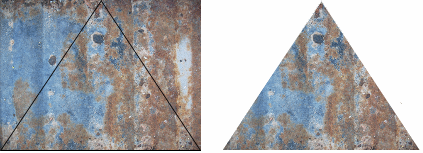


Kommentare (6)