Computergrafik – Teil 3

Übersetzt heißt das: jeder y-Wert einer Linie (die Höhe des Punktes) kann berechnet werden, indem der zugehörige x-Wert (die Breite des Punktes) in die Gleichung eingesetzt wird. Die Steigung m der Geraden kann berechnet werden, sobald wenigstens 2 Punkte bekannt sind; bei einem Liniensegment sind das für gewöhnlich der Anfangspunkt ( x_s, y_s )  und der Endpunkt  ( x_e, y_e ); m berechnet sich dann aus folgender Formel:

m = ( y_e – y_s ) / ( x_e – x_s )

Mit diesen Informationen lässt sich nun ein durch Start- und Endpunkt gegebenes Liniensegment auf den Bildschirm zeichnen. Da Pixel-Koordinaten immer ganzzahligen Werten entsprechen (sprich, 1, 2, 3 usw., aber nie zum Beispiel 1,5), muss man zum Zeichnen der Linie lediglich alle x-Werte zwischen Anfangs- und Endwert durchlaufen, für jeden den zugehörigen y-Wert berechnen und den so berechneten Pixel auf dem Bildschirm einfärben. Da für die y-Werte natürlich nicht zwangsläufig immer ganzzahlige Werte herauskommen, hilft einfaches Auf- bzw. Abrunden.

Schauen wir uns ein kurzes Beispiel an. Nehmen wir als Startpunkt des zu zeichnenden Liniensegments etwa den Punkt (1,1) und als Endpunkt den Punkt (9, 4). Aus diesen beiden Punkten lässt sich der Anstieg der Geraden folgendermaßen berechnen:

 m = ( 4 – 1 ) / ( 9 – 1 ) = 3 / 8 = 0,375

Die Geradengleichung lautet demzufolge (wobei man genauso gut den Endpunkt als Referenzpunkt benutzen könnte):

 y =
0,375
* ( x – 1 ) + 1

Nun muss für alle x-Werte von 1 bis 6 der zugehörige y-Wert berechnet werden; gerundet ergeben sich die folgenden Wertepaare (x,y):

(1,1), (2,1), (3,2), (4,2), (5,3), (6,3), (7,3), (8,4), (9,4)

Diese Pixelkoordinaten bilden das gerasterte Liniensegment; in ein Raster (also z.B. den Bildschirm) gezeichnet würden sie so aussehen (in Grau die Punkte, in Schwarz die originale Strecke zum Vergleich); Achtung: der Koordinatenursprung liegt informatikgerecht natürlich bei (0,0):

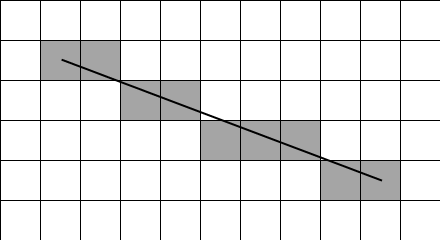
Man sieht, dass die gerasterten Punkte eine recht gute Annäherung an das eigentliche Liniensegment darstellen. Natürlich wirkt es ein wenig grob und eckig; es gibt zwar ausgefeilte Algorithmen, die diese Kante glätten können (Freunde von Computerspielen werden das als Antialiasing kennen), aber die sollen hier nicht weiter interessieren.

Da wir ja bereits im letzten Artikel geklärt haben, wie sich einzelne Punkte aus Welt- (3-dimensional) in Bildschirm-Koordinaten (2-dimensional) umrechnen lassen, haben wir jetzt das benötigte Handwerkzeug zusammen, um komplexe Objekte auf dem Bildschirm darstellen zu können. Ein Objekt wird, wie bereits erwähnt, durch eine Menge von Dreiecken beschrieben. Ein Dreieck ist aber nichts anderes als 3 Liniensegmente, die durch die drei Eckpunkte des Dreiecks begrenzt werden. Um also ein Dreieck auf den Bildschirm zu zeichnen, reicht es, die drei zugehörigen Linien zu zeichnen (durch dieses Verfahren ist auch das erste Bild im Artikel entstanden).²  Ein simples Beispiel hierzu (ohne Rechenweg), welches 4 Dreiecke zeigt (den Rest des Würfels möge man sich einfach denken):

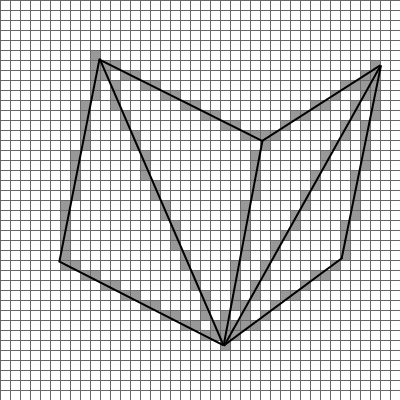
Aufmerksame Leser werden nun bemerken, dass ich ja eigentlich davon gesprochen hatte, dass für jeden x-Wert zwischen Start- und Endpunkt des Liniensegments ein y-Wert berechnet wird. Es sollte also nicht der Fall sein können, dass für ein Liniensegment einem y-Wert mehrere x-Werte zugeordnet sind; offensichtlich ist das aber in der Abbildung der Fall und auch gar nicht vermeidbar, um vernünftig Linien darstellen zu können. Der Trick dabei ist: sobald der Anstieg eines Liniensegmentes größer ist als 0,5 (oder kleiner als -0.5), wird die Geradengleichung einfach nach y umgestellt und stattdessen für jeden y-Wert zwischen Start- und Endpunkt ein x-Wert berechnet.

Am Bild ist übrigens auch gut zu erkennen, warum eine höhere Auflösung (das heißt, mehr gezeichnete Pixel in Breite und Höhe) gern gesehen wird: das Bild wird dadurch nämlich viel feiner und wirkt nicht so blockig wie obiges Beispiel.