Computergrafik – Teil 3

Nachdem im letzten Artikel (ich muss dringend an den Update-Zyklen arbeiten…) geklärt wurde, wie ein einzelner Punkt mit Hilfe von Matrizen so transformiert werden kann, dass er auf den Bildschirm gezeichnet werden kann, wollen wir uns heute damit beschäftigen, wie mit Hilfe dieser Technik ganze Objekte statt nur einzelner Punkte darstellbar sind. Natürlich ist es auch diesmal nicht ganz so einfach und es wird vorher noch etwas Mathematik benötigt, um die gewünschten Objekte nachher auch wirklich zeichnen zu können. Aber eins nach dem anderen.

Zur Darstellung von Objekten mit Hilfe von im Raum liegenden Punkten auf dem Bildschirm gibt es verschiedene Verfahren; die beiden Hauptverfahren habe ich beim letzten mal schon angedeutet. Zum einen wäre das die Verwendung sogenannter Punktwolken, bei denen die darzustellenden Objekte komplett durch viele Einzelpunkte beschrieben werden; diese Punkte – und damit das darzustellende Objekt – können mit dem bereits beschriebenen Verfahren auf den Bildschirm gezeichnet werden. Das funktioniert, hat aber den Nachteil, dass es relativ Speicher- und Rechenaufwändig ist, um die Detailgenauigkeit hinzubekommen, die gewünscht wird (auf Grund steigender Rechenkapazitäten ist es aber wahrscheinlich, dass dieser Ansatz in den nächsten Jahren verstärkt verfolgt wird). Momentan wird daher eher auf Polygonnetze (englisch Polygon Meshes, kurz Meshes) gesetzt.

Kurz zur Theorie: ein Polygon ist ein Vieleck, also eine Menge durch einen Linienzug verbundener Punkte. Das einfachste Polygon ist das allseits bekannte Dreieck, welches folgerichtig durch drei Punkte bestimmt wird. Derartige Dreiecke lassen sich relativ leicht auf den Bildschirm zeichnen (wie, sehen wir gleich noch), weswegen sie in der Computergrafik gern benutzt werden, um Objekte darzustellen. Zu diesem Zweck wird die Oberfläche eines Objektes durch eine Menge miteinander verbundener Dreiecke, das Polygonnetz, beschrieben; die Anzahl der verwendeten Dreiecke bestimmt dabei, wie detailliert ein Objekt beschrieben wird – je mehr Dreiecke, desto mehr Details. Unsere Szene aus dem letzten Artikel mit Dreiecken dargestellt würde etwa so aussehen (man spricht bei derartigen Darstellungen vom Drahtgittermodell, da es wirkt, als wären die Objekte aus dünnen Drähten aufgebaut):

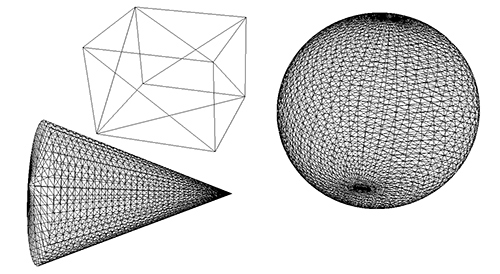
Zu beachten ist, dass der Würfel aus wenigen Dreiecken (konkret: 12) besteht, der Kegel und die Kugel dagegen aus einer ungleich größeren Menge; würden Kugel und Kegel aus weniger Dreiecken bestehen, wären sie nicht mehr so schön “rund”, sondern eher eckig und kantig – ganz so, wie man die Grafik aus älteren 3D-Computerspielen gewöhnt ist.

Nun wissen wir zwar, wie sich die Form eines Objektes durch Dreiecke beschreiben lässt (über Farben reden wir ein andermal), aber es bleibt immer noch die Frage, wie diese Dreiecke am Ende auf den Bildschirm kommen. Genau hier kommt nun die Technik zum Einsatz, die dem ganzen Verfahren seinen Namen gegeben hat, nämlich die Rasterung (engl. Rasterisation). Unter diesem Begriff werden mehrere Methoden zusammengefasst, um geometrische Objekte in eine Rastergrafik, also in ein aus Pixeln bzw. Punkten bestehendes Bild, umzuwandeln.

Die einfachste Methode der Rasterung ist natürlich das Zeichnen von Punkten; hierbei wird ein in Bildschirmkoordinaten vorliegender Punkt (also ein Punkt mit einer Angabe für die Position in Breite und Höhe) einfach in das Raster gesetzt (wie das funktionierte, wurde bereits hier beschrieben).

Der nächste Schritt wäre nun die Rasterung von Linien; das ist mathematisch ein wenig anspruchsvoller, aber immer noch recht einfach umzusetzen. Zur Rasterung einer Linie wird ihre geometrische
Beschreibung, bestehend aus Anfangs- und Endpunkt der Linie, als Grundlage für den Zeichenvorgang benutzt. Das einfachste Verfahren ist, die zu zeichnende Linie durch ihre Geradengleichung¹ zu beschreiben. Wir erinnern uns aus der Mathematik: eine Linie wird in der Geradengleichung durch ihren Anstieg m und einen Punkt (x_s,y_s) auf der Linie beschrieben (auch bekannt als Einpunktform):

y = m * ( x – x_s ) + y_s

^{1 An dieser Stelle ein kurzes Wort zur Terminologie: eine Strecke ist eine gerade Linie, die von 2 Punkten begrenzt wird. Eine Gerade ist eine unendlich lange gerade Linie. Der englische Ausdruck für “Strecke” ist “line segment” – ich werde daher auch im Deutschen von Liniensegmenten reden.}