Während meiner Auszeit erscheinen hier einige Gastbeiträge von anderen Bloggern. Wenn ihr auch Lust habt, euer Blog (euren Podcast, euer Videoblog, etc) hier vorzustellen oder einfach nur mal einen Artikel schreiben wollt, dann macht mit!
Heute gibt es einen Artikel von Alderamin.
In Science-Fiction-Storys ist die interstellare Raumfahrt ein Klacks. Sie bildet dort den Hintergrund für die Geschichten, die auf dem Kontakt mit Lebewesen fremder Planeten aufbauen. Es wird dort normalerweise nicht hinterfragt, wie aufwändig interstellare Reisen eigentlich sind – die Raumschiffe haben irgendeinen kompakten Antrieb, der sie auf geheimnisvolle Weise mit irrsinniger Geschwindigkeit durch den Weltraum befördert. Die Lichtgeschwindigkeit wird mit irgendwelchen technischen Tricks ausgehebelt. Im Folgenden soll gezeigt werden, welche Probleme für die interstellare Raumfahrt tatsächlich zu lösen sind. Die Zahlen in diesem Artikel beruhen auf einem Kapitel in Meyers Handbuch Weltall, 5. Auflage, 1973. Obwohl das Buch schon recht alt ist, sind die angegebenen Zahlen prinzipieller Natur und werden auch in Zukunft weiterhin gültig sein.
Das Ziel
Erst seit Mitte der 1990er ist es uns technisch möglich, Planeten anderer Sterne nachzuweisen. Der Satellit Kepler sammelt derzeit statistische Daten über die Häufigkeit verschiedener Arten von Exoplaneten. Es scheint so zu sein, als ob die meisten Sterne wenigstens einen Gesteinsplaneten von Erdgröße haben. Nach einer Hochrechnung von Wesley Traub, der leitender Wissenschaftler beim Exoplanet Exploration Program der NASA ist, könnten 34% aller sonnenähnlichen Sterne erdähnliche Planeten in der habitablen Zone haben, d.h. in einem Abstand, der flüssiges Wasser erlauben würde. Das passt ganz gut zu den Zahlen aus Meyers Handbuch Weltall: dort wird von 50% der sonnenähnlichen Sterne angenommen, dass sie erdähnliche Planeten in der habitablen Zone haben, aber man beschränkt sich auf Einzelsterne, die 40% aller Sternsysteme ausmachen, das wären dann 20% der sonnenähnlichen Sterne mit Planeten in der habitablen Zone. Sehr optimistisch gehen die Autoren davon aus, dass diese Planeten alle bewohnbar seien – dabei hatte selbst unsere Erde nur während der jüngsten 13% ihrer Lebensdauer eine Atmosphäre mit mehr als 5% Sauerstoffgehalt. Aber übernehmen wir die Zahlen einfach mal so und berücksichtigen, dass nur 30% der Sterne „sonnenähnlich genug” sind (Spektralklasse F5V bis M1V), dann kommt man insgesamt auf 6% Anteil bewohnbarer Planeten gemessen an der Zahl aller Sterne.
Die Entfernungen
Die 10 nächsten dieser 6% sind im Mittel 5,6 parsec oder 18,3 Lichtjahre entfernt – so weit müssten wir fliegen, um einen bewohnbaren Planeten zu erreichen.
Der Abstand zweier gleichzeitig existierender Zivilisationen wäre jedoch viel größer. Wir wissen nicht, wie wahrscheinlich es ist, dass ein bewohnbarer Planet auch intelligentes Leben hervorbringt. In Meyers Handbuch geht man von 100% aus, was mir viel zu optimistisch erscheint, aber seien wir auch hier einfach mal so optimistisch, wir wollen ja keine Miesmacher sein. Darüber hinaus wird die mittlere Lebensdauer einer Zivilisation mit 100 000 Jahren angenommen. Mit diesen Annahmen kommt man auf eine augenblicklich existierende Zivilisation pro 1 Million Sterne und einen mittleren Abstand von 250 parsec oder ca. 800 Lichtjahren dorthin. So weit müssten andere Zivilisationen im Mittel fliegen, um uns zu erreichen.
Ein Lichtjahr ist eine gewaltige Entfernung. Könnte ein Linienjet, der uns in 2 Stunden nach Mallorca, in 10 Stunden in die USA und in 24 Stunden auf die gegenüberliegende Erdseite nach Australien bringt, bis zur Sonne fliegen, er wäre 19 Jahre ununterbrochen unterwegs. Ein Lichtstrahl schafft die Strecke in nur 8 Minuten 20 Sekunden. Die Fixsterne sind so unglaublich weit entfernt, dass sie sich am Himmel nur messbar, aber nicht sichtbar verschieben während die Erde bei ihrem jährlichen Lauf um die Sonne ihre Position um den doppelten Sonnenabstand variiert (nämlich den Durchmesser ihrer Bahn um die Sonne). Der Abstand zum nächsten Stern ist 287 400 mal so groß wie der Abstand der Erde zur Sonne: 43 000 Milliarden Kilometer oder 4,3 Lichtjahre. Ein Viertel der Strecke, die wir uns vorgenommen haben…
Der Zeitfaktor
Die Lichtgeschwindigkeit kann leider nicht überschritten werden; das wissen wir spätestens seit Einsteins spezieller Relativitätstheorie. Wenn ein beliebiges Objekt von einer Kraft beschleunigt wird, dann wird es zunächst schneller. Wenn die Geschwindigkeit sich nennenswerten Bruchteilen der Lichtgeschwindigkeit nähert, kommt jedoch ein weiterer Effekt hinzu: es wird massiver und damit träger. Je näher man sich der Lichtgeschwindigkeit nähert, desto weniger trägt eine weitere Energiezufuhr zur Geschwindigkeitserhöhung bei, vielmehr steigt die Masse ins Unermessliche. Deswegen kann man sich der Lichtgeschwindigkeit zwar theoretisch beliebig nahe annähern, aber sie niemals erreichen oder gar überschreiten. Das ist auch experimentell hervorragend bestätigt, denn wir können in Teilchenbeschleunigern Teilchen auf 99,99999% der Lichtgeschwindigkeit beschleunigen, und durch mehr Energieaufwand immer mehr 9en hinter dem Komma anfügen, aber die Teilchen werden dabei tausende Male massiver als sie im Ruhezustand sind. Die Lichtgeschwindigkeit erreichen dennoch nicht.
Das Licht schafft es, die Strecke zum nächsten Stern in 4,3 Jahren zurück zu legen, das klingt zunächst mal machbar. Die 18,3 Lichtjahre zu einem bewohnbaren Planeten wären auch noch drin, wenn man so lange in einer Röhre ausharren will, und sei es im Tiefschlaf. Bei den 800 Jahren, die das Durchschnitts-UFO zu uns bräuchte, wären allerdings schon Methusalem-Aliens gefragt.
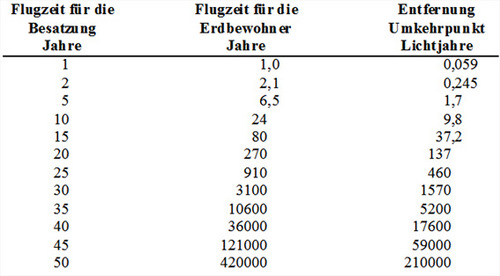
Diese Flugzeiten gelten allerdings nur aus Sicht der daheim Gebliebenen. Die spezielle Relativitätstheorie spielt uns hier in die Hände, denn ein sich mit einem nennenswerten Bruchteil der Lichtgeschwindigkeit bewegendes Objekt wird nicht nur massiver, sondern seine Zeit scheint um den gleichen Faktor verlangsamt abzulaufen. Ohne hier auf die Details der Zeitdilatation und des Zwillingsparadoxons einzugehen, sei an dieser Stelle einfach die Tabelle aus Meyers Handbuch zitiert, bei der man davon ausgeht, dass die Hälfte der Strecke konstant mit der einfachen Erdbeschleunigung beschleunigt wird und auf der zweiten Hälfte der Strecke (Umkehrpunkt) das Raumschiff gewendet und mit dem gleichen Wert verzögert wird – dann herrschte an Bord stets einfache Erdgravitation:
Das schaut ja ganz ermutigend aus: mit 45 Jahren Bordzeit könnte man bis ans gegenüber liegende Ende der Milchstraße gelangen, die ca. 100 000 Lichtjahre durchmisst. Doch dem liegt eine unrealistische Annahme zu Grunde: dass wir 50 Jahre lang ununterbrochen die Beschleunigung eines Formel-1-Wagens aufrecht erhalten könnten…
Der Antrieb
Wenn wir uns im Weltraum vorwärts bewegen wollen, gibt es als Antriebsquelle nur den Rückstoß. Auch Konzepte wie Sonnensegel oder ein Laserstrahl von der Erde, der das Raumschiff anschieben soll, basieren auf dem Rückstoß, aber sie taugen nicht für die gewaltigen interstellaren Entfernungen, und zum Abbremsen müsste der Schub aus der Gegenrichtung kommen. Also kommt nur Rückstoß durch mitgenommenen Treibstoff in Frage.
Das Problem dabei ist, dass man riesige Mengen Treibstoff benötigt, die selbst eine große Masse mit sich bringen, welche selbst wiederum beschleunigt werden muss. Chemischer Treibstoff ist dabei nicht sehr effizient. Z.B. bringt die Verbrennung von 273 g Kohlenstoff (Kerosin, Flugbenzin) mit 727 g Sauerstoff (also 1 kg Treibstoff, auch der Sauerstoff muss, anders als beim Flugzeug, mitgenommen werden) eine Energie von 2,64 kWh. Um 1 kg Brennstoff überhaupt von der Erde in den Weltraum zu befördern, benötigt man jedoch 17,4 kWh, das entspricht einer Treibstoffmasse von 6,56 kg! Wasserstoff-Sauerstoff-Verbrennung ist ein wenig effizienter, aber nicht viel. Dass das ganze überhaupt funktioniert, liegt einzig und alleine daran, dass man fast den gesamten Treibstoff auf dem Weg in den Weltraum ausstößt und mit einer weit gehend leeren Rakete oben ankommt.
Wie dies funktioniert, zeigt die Raketengleichung von Ziolkowski. Diese lautet:
V = ln M
wobei V = v(end) / s das Geschwindigkeitsverhältnis aus erreichter Endgeschwindigkeit v(end) zur Ausströmgeschwindigkeit s und M das Massenverhältnis aus dem Startgewicht der Rakete (Rakete voll mit Treibstoff beladen) zum Leergewicht (nur die Nutzlast und Struktur wie Tanks, Triebwerke, Druckpumpen, Hülle etc.) ist. Entscheidend ist hierbei die Ausströmgeschwindigkeit: die mit einem bestimmten Masseverhältnis erreichte Endgeschwindigkeit steigt in gleichem Maße wie die Ausströmgeschwindigkeit. Bei chemischen Antrieben liegt diese bei 2,5 km/s, was nicht viel ist, wenn man z.B. zum Mond möchte, wofür die Fluchtgeschwindigkeit der Erde von 11,2 km/s überwunden werden muss. Dies schafft man mit einem Massenverhältnis von 88: Die Nutzlast macht nur 1,13% des Gesamtgewichts aus! Dies gilt allerdings nur für eine einstufige Rakete. Bei einer mehrstufigen Rakete sind die oberen Stufen die Nutzlast der unteren, die alle bis auf die eigentliche Nutzlast unterwegs abgeworfen werden und somit zählt ihre Struktur nicht mehr zum letztlich verbliebenen Leergewicht. Das Massenverhältnis der einzelnen Stufen multipliziert sich in diesem Fall, die Endgeschwindigkeiten addieren sich. Abgesehen davon, dass jede Stufe ihren eigenen Antrieb mitschleppen muss, hat dieses Prinzip aber auch seine theoretischen Grenzen, mehr als 4 Stufen bringen kaum noch Gewinn, die Endgeschwindigkeit wird weniger als verdoppelt. In die Nähe der Lichtgeschwindigkeit kommt so auf keinen Fall.
Chemische Antriebe
Man müsste vielmehr die Ausströmgeschwindigkeit erhöhen. Bei chemischer Verbrennung hängt diese direkt mit der Temperatur der verbrannten Gase zusammen, die sich unter hohem Druck in Grenzen erhöhen lassen. In der Praxis verwendet man heute z.B. Wasserstoff + Sauerstoff bei 4000 °C – mehr hält kein Material einer Düse aus, und eine Düse braucht es zum Aufbau des Drucks – welche eine Ausströmgeschwindigkeit von 3,97 km/s ergeben. Es ergibt sich ein benötigtes Massenverhältnis von 17 für 11,2 km/s Endgeschwindigkeit, bzw. 65 für 16,6 km/s. In Summe mit der Erdbahngeschwindigkeit bei einem Start in Richtung der Erdbewegung um die Sonne würde man mit diesem Wert die Fluchtgeschwindigkeit der Sonne zum Verlassen des Sonnensystems erreichen. Bei dieser Geschwindigkeit dauerte es allerdings hunderttausende Jahre zu den nächsten Sternen.
Kernfusion
Welche Alternativen wären denkbar? Die elektrischen Ionenantriebe brauchen wir hier gar nicht zu betrachten, sie sind zwar effizienter, aber für die interstellare Raumfahrt bei weitem nicht genug. Vielleicht kann man jedoch eines Tages die bei der Kernfusion frei werdende Energie direkt in Schubkraft umwandeln, indem die fusionierten Heliumkerne mit der Energie der Kernverschmelzung als Schubstrahl ausgestoßen werden. Das wäre so ziemlich der effizienteste, noch als realisierbar vorstellbare Rückstoßantrieb. 1 g fusionierter Wasserstoff würde etwa 100 Milliarden Joules Energie liefern. Wenn man das Helium mit dieser Energie ausstoßen könnte, käme man auf eine Strahlgeschwindigkeit von immerhin 8,2% der Lichtgeschwindigkeit. Bei einem Massenverhältnis von 10 ergäbe sich eine Endgeschwindigkeit von 18,9% der Lichtgeschwindigkeit; bei dieser Geschwindigkeit spielt die Zeitdilatation mit einem Faktor von 1,02 noch keine Rolle. Für den Hin- und Rückflug ergäben sich somit kombinierte Hin- und Rückflugzeiten von
– 180 Jahren für 18,3 Lichtjahre
– 8000 Jahren für 800 Lichtjahre
Wobei wir noch keinen Gedanken daran verschwendet haben, wie bewerkstelligt werden soll, dass die fusionierten Teilchen diese Energie überhaupt als Impuls in Schubrichtung erhalten, entsteht doch bei der Fusionsreaktion hauptsächlich Gammastrahlung, die in alle möglichen Richtungen abgegeben wird.
Zerstrahlung der Materie
Die effizienteste denkbare Energiequelle wäre die Zerstrahlung von Antimaterie. Dabei würde eine Energiemenge von E = m c² frei – im Idealfall würde der gesamte Treibstoff in reine Energie in Form von Gammastrahlung verwandelt (Antimaterieatome und Atome normaler Materie zerstrahlen nicht, wie Positronen und Elektronen, komplett zu Gammastrahlung, sondern zu Pi-Mesonen + Gammastrahlung, weil die Baryonenzahl eine Erhaltungsgröße ist). 1 g zerstrahlter Materie/Antimaterie lieferte die ungeheure Energiemenge von 90 Billionen Joules – etwa so viel wie bei der Atombombe von Nagasaki frei gesetzt wurden (21 kt TNT-Äquivalent).
Bei einem lichtschnellen Antriebsstrahl in Form der entstandenen Gamma-Photonen ändert sich die Raketengleichung wie folgt:
V = tanh (ln M)
wobei hier das Geschwindigkeitsverhältnis V = v(end)/c ist, also der Bruchteil der erreichten Lichtgeschwindigkeit c. Setzen wir wieder ein Massenverhältnis von 10 an, so erhalten wir eine Endgeschwindigkeit von 98% der Lichtgeschwindigkeit, ganz gleich, welche Beschleunigung verwendet wird. Wenn wir eine kontinuierliche Beschleunigung von 1 G voraussetzen, dann würde der Treibstoff für 2,34 Jahre Bordzeit oder 5,03 Jahre Erdzeit reichen. Flöge die Rakete danach mit konstanter Geschwindigkeit weiter, dann verginge die Zeit an Bord um den Faktor 5,04 verlangsamt und es ergäben sich kombinierte Hin- und Rückflugzeiten von
– 14 Jahren Bordzeit / 42 Jahren Erdzeit für 18,3 Lichtjahre
– 300 Jahren Bordzeit / 1600 Jahren Erdzeit für 800 Lichtjahre
Das heißt, so gerechnet wären die nächsten habitablen Planeten gerade noch erreichbar, die (optimistisch geschätzt) nächsten Planeten mit intelligentem Leben jedoch bereits für einen lebenden Menschen unerreichbar. Man könnte vielleicht ein Generationenschiff dorthin senden, oder eine Möglichkeit finden, Menschen für Jahrhunderte einzufrieren, aber Ausflüge á la Raumschiff Enterprise ans andere Ende der Milchstraße wären gänzlich undenkbar.
Technische Probleme
Hinzu kommt, dass die Beschleunigung von 1 G auch irgendwie in Form eines entsprechenden Schubs erreicht werden muss. Ein Scheinwerfer mit 10 kW Leistung erzeugt z.B. nur einen Strahlungsdruck von 3,5 mg. Um eine Schubkraft von 1/100 N (1 g) zu erreichen, bräuchte es 3000 kW, also 3 Megawatt – damit ließe sich gerade mal 1 Gramm Masse mit 1 G beschleunigen. Wenn wir von einem Massenverhältnis von 10 ausgehen, dann muss zu Beginn das Zehnfache der unbetankten Raumschiffmasse beschleunigt werden, wofür eine Leistung von 60 MW/g aufgebracht werden müsste. Heutige Antriebe leisten etwa 300 W/g, das entspricht für die Gesamtmasse der Rakete nur 30 W/g. Um die Forderung 60 MW/g zu erfüllen, dürfte ein Automotor von 100 PS nur 1 mg wiegen und ein Atomkraftwerk von 300 MW nur 5 g. Diese Anforderungen an das Verhältnis Leistung zu Masse lassen sich prinzipiell nicht umgehen und werden wahrscheinlich niemals erfüllt werden können.
Ein weiteres Problem betrifft die Lagerung des Treibstoffs. Antimaterie besteht aus den Antiteilchen der normalen Materie und verhält sich isoliert im Prinzip genau so, wie diese. Es gibt also z.B. Antiwasserstoff, bestehend aus einem negativ geladenen Antiproton im Kern umkreist von einem positiv geladenen Anti-Elektron (Positron) – ein paar Atome dieses Stoffs wurden bereits in Beschleunigern erzeugt; derzeit allerdings mit einer Rate, die Milliarden Jahre für ein einziges Gramm benötigen würde. Materie und Antimaterie zerstrahlen jedoch bei jeglichem Kontakt sofort und unvermeidlich und somit ist Antimaterie in makroskopischer Menge der gefährlichste vorstellbare Stoff überhaupt. Wie oben gezeigt, entwickelt 1 Gramm dieses Stoffes bereits die Sprengkraft einer Atombombe. Einzelne geladene Antiteilchen (Antiprotonen, Positronen) ließen sich zwar mit elektrischen Feldern einschließen, aber diese Teilchen stoßen sich stark untereinander ab und in geladener Form könnte man sie nur als dünnes Gas in einem riesigen Volumen aufbewahren – man bräuchte jedoch eine stark komprimierte Form, um das Raumschiff klein und leicht halten zu können, was nur bei neutralen Teilchen möglich wäre, die wiederum elektromagnetische Felder kaum spüren. Eine denkbare Variante wäre das Einfrieren von Antiwasserstoff, der (wie normaler Wasserstoff) schwach diamagnetisch ist und somit von sehr starken Magnetfeldern schwebend gehalten werden könnte. Aber selbst auf 1 K gekühlter (Anti-)Wasserstoff würde schwach sublimieren (verdunsten) und die neutralen Anti-Atome würden das Behältnis angreifen. Ein kurzfristiger Ausfall der Haltemagneten würde zur sofortigen Zerstörung des Raumschiffs führen, und das Risiko bestünde über eine Flugzeit von vielen Jahren.
Daneben besteht noch das Problem, dass das Weltall Staub und Mikrometeoriten enthält. Wenn ein kleiner Splitter mit nahezu Lichtgeschwindigkeit vom Raumschiff getroffen würde, dann hätte er eine Einschlagsenergie in der Größenordnung seiner Masse umgewandelt in reine Energie und würde dieses komplett durchschlagen. Träfe er den massiven, gefrorenen Antimaterie-Treibstoff, aus dem 40% der Raumschiffmasse bestünden, würde dieser ebenfalls sofort explodieren und das Generationenschiff hätte sich erledigt. Deswegen scheint mir die Wasserstofffusion, wie oben erwähnt, die einzig praktikable Möglichkeit für einen realistischen interstellaren Antrieb.
Höhere Dimensionen?
Zuletzt noch ein Wort zu Wurmlöchern, Warpantrieben und dergleichen. Science-Fiction-Autoren sind einfallsreich darin, sich Auswege zu überlegen, wie man sich diesen Problemen entziehen könnte. In einigen Storys fliegt man einfach durch eine fünfte Dimension. Dem Leser sollte allerdings bewusst sein, dass es sich hierbei lediglich um Fiktion handelt. Selbst wenn es – wie in der Stringtheorie – höhere Dimensionen geben sollte, dann heißt das nicht notwendigerweise, dass man sich in diesen auch bewegen könnte, dass dort die Lichtgeschwindigkeit überschritten werden könnte oder der Weg kürzer wäre. Am ehesten mit der Physik verträglich wären Wurmlöcher. Jedoch bräuchte es zu ihrer Erzeugung ein Material mit negativer Energiedichte, sogenannte “exotische Materie”, und davon für ein Wurmloch mit einem Meter Durchmesser nicht weniger als eine Jupitermasse. Angesichts der Tatsache, dass es solche Materie wahrscheinlich gar nicht gibt, erscheinen die Probleme des Flugs mit Antimaterie-Zerstrahlung geradezu trivial. Mit Warp-Antrieben sieht es nicht viel besser aus. Man mag argumentieren, dass unser Wissen über die Physik einfach noch zu begrenzt sei, aber dem ist entgegen zu halten, dass die Dinge, die wir z.B. über die Lichtgeschwindigkeit als oberste Grenze wissen, deswegen nicht mehr falsch werden – auch gilt trotz Einstein noch Newtons Gravitationsgesetz in seinen Grenzen. Wir wissen schon eine ganze Menge, und das was wir wissen, schließt interstellare Raumfahrt leider weitgehend aus.
Fazit
Die interstellare Raumfahrt ist leider sehr viel schwieriger zu bewerkstelligen, als Science-Fiction-Filme uns weismachen wollen. Das mag frustrieren, aber das Weltall ist nicht entstanden, um uns Billigflüge an jeden Ort der Milchstraße zu ermöglichen. Insofern wäre es auch für andere Wesen ausgesprochen schwierig, unseren Planeten zu erreichen, wobei mir die 800 Lichtjahre Abstand ohnehin viel zu optimistisch erscheinen. Es könnte genau so gut sein, dass es augenblicklich nur eine handvoll Intelligenzen in der Milchstraße gibt, oder gar, dass wir die einzigen sind. Wenn eine Intelligenz sich auf den Weg in den Raum zwischen den Sternen machen sollte, dann wird sie dies sicher nicht leichtfertig und zum Spaß tun, sondern mit zwingendem Hintergrund, z.B. um ihre Art zu retten. Sie wäre uns weit überlegen und würden sich nicht vor uns verstecken müssen. Eine Rückkehr oder ein Flug zu einem anderen bewohnbaren Planeten wäre viel zu aufwändig. Sie kämen gezielt zu uns, und sie kämen, um zu bleiben.











Kommentare (644)