Warum fallen Satelliten nicht vom Himmel? Blöde Frage – warum sollten sie? Sie befinden sich im Orbit um die Erde; bewegen sich also so schnell “seitwärts”, dass sie trotz der Gravitationskraft der Erde nicht zurück auf den Erdboden stürzen, sondern quasi ständig an der Erde vorbei fallen (deswegen heißt das ja auch “freier Fall”). Die Gesetze von Johannes Kepler und Isaac Newton erklären genau, wie diese Bewegung beschrieben werden muss. Und weil wir wissen, wie sich Satelliten bewegen müssen, damit sie nicht runterfallen, fallen unsere Satelliten auch nicht vom Himmel. Klingt einfach; ist in Wahrheit aber ein klein wenig komplizierter. Denn wir wissen zwar tatsächlich, auf welche Bahn man einen Satelliten schicken muss, damit er oben bleibt. Wir wissen aber nicht, warum sie das tun. Zumindest nicht so genau, wie man es vielleicht gerne wissen will. Aber das hat sich jetzt geändert.
Scott Tremaine und Tomer Yavetz von der Universität Princeton haben kürzlich eine Arbeit veröffentlicht, in der sie genau vorrechnen, warum Satelliten nicht vom Himmel fallen (“Why do Earth satellites stay up?”). Das mag ein wenig seltsam klingen. Immerhin wurde der erste Satellit schon im Jahr 1957 ins All geschickt und dem Sputnik sind ein paar tausend weitere künstliche Himmelskörper gefolgt, die die Erde umkreisen. Die Satellitentechnik ist Teil unseres Alltags geworden und da erscheint es ein wenig komisch, dass offensichtlich immer noch Bedarf an einer Erklärung besteht, die uns sagt, warum die Dinger oben bleiben und nicht ständig abstürzen.
Die Sache ist ein bisschen kompliziert. Zuerst muss man sich klar machen, dass es keine exakte Beschreibung der Bewegung von Satelliten geben kann. Es ist unmöglich, die Bewegung von mehr als zwei Himmelskörpern bis ins letzte Detail zu beschreiben. Nicht, weil wir zu dumm dazu sind oder die Sache noch nicht auf die Reihe gekriegt haben. Sondern weil es mathematisch unmöglich ist. Der Mathematiker Henri Poincaré hat 1888 bewiesen, dass es keine Möglichkeit gibt, die Bewegung der Himmelskörper für alle Zeitpunkte in der Zukunft exakt vorherzusagen. Die wechselseitige gravitative Anziehung zwischen den Planeten macht die Sache so kompliziert, dass sich die entsprechenden Gleichungen nicht lösen können (Wer mehr zu den mathematischen Aspekten dieses Themas erfahren will, kann meine Serie über Störungsrechnung lesen: Teil 1, Teil 2, Teil 3, Teil 4).
Wenn es also darum, die Bewegung von Himmelskörpern – egal ob künstlich oder natürlich – zu beschreiben, dann ist diese Beschreibung zwangsläufig immer nur eine Näherung. Und die Wissenschaftler haben es in den letzten Jahrzehnten gut verstanden, die Bahnen der Satelliten so gut zu beschreiben, um sicherzustellen, dass sie nicht wieder runterfallen. Man weiß, wo und wie sich die künstlichen Objekte bewegen müssen, um ausreichend lange auf stabilen Bahnen zu bleiben damit sie ihren jeweiligen Job erledigen können. Aber obwohl die Keplerschen Gesetze gut genug sind, um Satelliten in einen Orbit zu bringen, reichen sie nicht für eine umfassende Beschreibung der Realität. Es gibt jede Menge Störungen, die nicht von Keplers Gesetzen beschrieben werden und die könnten Probleme schaffen.

Die Erde ist keine perfekte Kugel. Die Abweichungen sind in diesem Bild allerdings stark übertrieben dargestellt (Bild: ESA)
Wäre die Erde zum Beispiel exakt kugelförmig, würden die Satelliten die sie umkreisen Bahnen einnehmen, auf denen Energie und Drehimpuls erhalten bleiben. Das heißt nichts anderes, als dass die Bahn selbst stabil ist. Wäre die Energie zum Beispiel nicht erhalten, würde die Bahn immer größer (oder kleiner) werden bis es irgendwann zur Kollision kommt. Genauso würde eine Verletzung der Drehimpulserhaltung dazu führen, dass die Bahn des Satelliten immer stärker von der Kreisform abweichen, bis sie irgendwann so langgestreckt sind, dass es ebenfalls zu einer Kollision kommt. Allerdings ist Erde keine perfekte Kugel. Sie ist ein wenig deformiert (wenn auch nur wenig) und deswegen sind Energie und vor allem Drehimpuls nicht exakt erhalten. Die unregelmäßige Form der Erde spielt keine Rolle, wenn man sich weit genug von ihr entfernt. Aus großer Distanz ist nur noch die gesamte Gravitation der Erde zu spüren und ihre Form spielt keine Rolle. In der Nähe ist das anders: Durch die unregelmäßige Form der Erde spürt der nahe Satellit eine unterschiedlich starke Gravitationswirkung, je nachdem über welchen Bereichen des Planeten er gerade hinweg fliegt.
Scott Tremaine und Tomer Yavetz haben in ihrer Arbeit untersucht, wie sich die Abweichung der Erde von der Kugelform auf die Satellitenbahnen auswirkt und warum die Bahnen stabil bleiben, obwohl Energie und Drehimpuls nicht erhalten bleiben. Wir wissen ja, dass die Bahnen stabil sind. Aber Tremaine und Yavetz wollten eine mathematische Beschreibung finden, die auch erklärt, warum das so ist. Dazu haben sie die Multipolentwicklung des Gravitationspotential untersucht und das ist gar nicht so kompliziert, wie es vielleicht klingt…
Eine Mulitpolentwicklung besteht aus einer Reihe immer besser werdender Näherungen. Bei der Erde geht man in erster Näherung davon aus, dass sie eine perfekte Kugel ist und modifiziert diese Näherung durch immer weitere Abweichungen. Mathematisch werden diese Abweichungen durch Koeffizienten beschrieben, die mit dem Buchstaben “J” bezeichnet werden. “J0” ist die vorhin schon erwähnte erste Näherung durch die Kugelform. “J1” beschreibt die erste Modifikation, bei der die Kugel durch eine Ellipsoid ersetzt wird. Da aber bei einem perfekten Ellipsoid Nord- und Südhälfte ebenfalls genau gleich schwer sind, ergibt sich hier keine Änderung zur ersten Näherung. Die kommt erst bei Berücksichtigung des Koeffizienten “J2”. Der beschreibt die Abweichungen die entstehen, wenn man die Erde als abgeplattetes Ellipsoid beschreibt. Misst man den Radius der Erde vom Mittelpunkt bis zum Äquator, dann ist dieser Wert um 21,38 Kilometer länger als der Radius, den man vom Mittelpunkt zu einem der beiden Pole misst. Nimmt man es genau, dann ist die Erde aber auf Nord- und Südhälfte unterschiedlich stark abgeplattet und diese Abweichung berücksichtigt der Koeffizient “J3”. Und so geht es dann immer weiter. “J4”, “J5”, “J6” und so weiter berücksichtigen immer weitere Abweichungen von der perfekten Kugelform. Um die Gravitationskraft der Erde exakt beschreiben zu können, müsste man all diese unendlich vielen Koeffizienten aufsummieren. In der Praxis ist das aber nicht möglich – und auch nicht nötig. Die Abweichungen werden immer kleiner und wirklich relevanten Einfluss haben nur die ersten paar Koeffizienten.
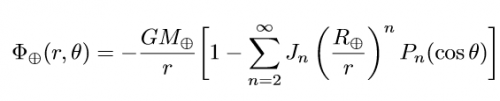
Die korrekte Beschreibung des Gravitationspotentials enthält eine unendliche Summe von Koeffizienten, die die Abweichungen von der Kugelform beschreiben (Formel aus dem Artikel von Tremaine und Yavetz)
Tremaine und Yavetz haben in ihrer Arbeit den Einfluss der ersten drei Koeffizienten untersucht. Sie haben mathematisch berechnet, wie stark die jeweiligen Abweichungen der Erde von der perfekten Kugelform die Stabilität der Satellitenbahnen beeinflussen. Dabei hat sich gezeigt, dass die Berücksichtigung von J2 die Bahnen nicht destabilisiert. Die Abplattung der Erde hat keinen störenden Einfluss auf die Bewegung von Satelliten. Nur wenn die Bahn des Satelliten gegen über dem Äquator um 63,43 Grad geneigt ist, kann es Probleme geben. Das ist die sogenannte “critical inclination” wo andere Störungen zu stark werden und Satellitenbahnen instabil. Auch die Abweichungen der Form der Erde, die durch J3 und J4 beschrieben werden, destabilisieren die Bahnen von Himmelskörpern. Ihr Einfluss ist aber viel geringer als der Einfluss von J2 und deswegen sind die Bahnen insgesamt stabil.
Wie gesagt: Das war auch schon vorher bekannt. Wir haben gewusst, dass die Bahnen der künstlichen Himmelskörper stabil sind. Aber nun haben Tremaine und Yavetz auch mathematisch vorgerechnet, warum das so ist und genau gezeigt, wie stark die einzelnen Störungen die Bewegung der Satelliten beeinflussen. Sie haben gezeigt, dass die Störungen zwar vorhanden sind, aber zu klein um die Bahnen deutlich zu destabilisieren. Die stärkste Abweichung der Erde von der Kugelform ist die Abplattung die durch den Koeffizienten J2 beschrieben wird und genau diese Abweichung hat keinen negativen Einfluss auf die Satellitenbahnen. Die Satelliten fallen also nicht vom Himmel und jetzt wissen wir auch, warum das so ist.












Kommentare (33)