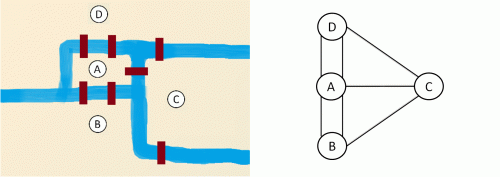
Zurück in die Gegenwart: Um die Lösungssuche voranzutreiben, wandte sich der damalige Bürgermeister der Stadt Danzig an den Schweizer Mathematiker Leonard Euler. Bald erkannte dieser, dass das Stadtzentrum vom Fluss in vier Teile zerschnitten wird. So bezeichnete er auf einer Skizze jeden Stadtteil mit einem Buchstaben und zeichnete die Brücken als Striche zwischen den einzelnen Buchstaben ein. Was er erhielt, gilt als der allererste Graph – und damit war das die Geburtsstunde der Graphentheorie.
Ein Graph – das sind Punkte (in unserem Fall die Stadtteile), die durch Striche (Brücken) miteinander verbunden sind. Alle Punkte eines Graphen müssen irgendwie zusammenhängen – das ist eine Regel. Es darf quasi keine Stadtteile geben, die für die Fußgänger unerreichbar sind. Das macht auch Sinn; außer man baut extra einen Hafen, um eine Brücke zu vermeiden … Eine zweite Regel besagt, dass sich zwei Striche nicht kreuzen dürfen – außer natürlich in einem Punkt. Wenn sich also zwei Striche treffen, muss dort demnach auf jeden Fall ein Punkt sein.
Mit seinem Graphen konnte Euler in einer Arbeit aus dem Jahre 1736 erklären, warum alle Bemühungen der Königsberger vergeblich waren und auch vergeblich bleiben würden: Einen solchen Spaziergang konnte es gar nicht geben! Natürlich behauptete er das nicht, ohne es rigoros zu untermauern: Ein Spaziergang wäre genau dann möglich, schrieb er, wenn höchstens zwei Punkte mit einer ungeraden Zahl von Strichen verknüpft wären (die restlichen mit einer geraden Zahl von Strichen). In Königsberg ist das jedoch nicht der Fall, da kein einziger der Stadtteile A, B, C oder D mit einer geraden Anzahl an Brücken verbunden ist. Wer sich gerne noch weiterhin mit dem „Königsberger Brückenproblem“ beschäftigen möchte, könnte eine Karte des heutigen Königsbergs betrachten: Zwei Brücken des Stadtzentrums wurden im Zweiten Weltkrieg zerstört. Ist dadurch vielleicht ein Spaziergang möglich geworden?
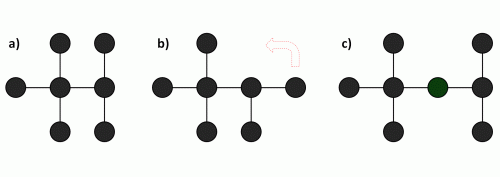
Jetzt aber zurück zum Rätsel: Es geht also darum, ganz spezielle Bäume zu zeichnen. Natürlich keine Buchen, Tannen oder Flaumeichen, sondern „mathematische“ Bäume. Das sind Graphen, in denen es keine Kreise gibt. Was bedeutet das? – Sehen wir uns noch einmal Eulers Graph an: Wir können vom Punkt A zu Punkt C spazieren, von Punkt C zu Punkt B, und kommen (über einen der beiden Striche) von B nach A zurück. Wir sind also zu unserem Startpunkt zurückgekehrt, ohne irgendwo „rückwärts gehen“ zu müssen. Wenn man das kann, muss es offensichtlich einen Kreis im Graphen geben. Eulers Graph ist folglich kein Baum, sehr wohl aber die drei Graphen in diesem Bild:
Die Bäume in unserem Rätsel sollen zudem vom Grad 10 sein. Das bedeutet, dass die Bäume aus genau 10 Punkten bestehen müssen – nicht aus mehr und nicht aus weniger. Ein Beispiel: Baum a und Baum b sind vom Grad 7, Baum c vom Grad 8.
Außerdem sollen die Bäume homöomorph irreduzibel sein. In unserem Fall bedeutet das ganz einfach, dass ein Punkt nicht mit genau zwei anderen Punkten verbunden sein darf. Warum das eine sinnvolle Einschränkung ist, sehen wir an Baum c: Achten wir auf den grünen Punkt! Im Grunde ist er ja vollkommen unnötig. Man müsste den Strich dort nicht unterbrechen, da ihn weder ein anderer Strich kreuzt noch ein Strich von ihm abzweigt. Um diesen Baum homöomorph irreduzibel zu machen, muss also der grüne Punkt entfernt werden (was uns geradewegs zu Baum a führt). Mit dieser Regelung bekommt man auch das „Punkte-Schinden“ in den Griff. Denn dort, wo der grüne Punkt ist, könnte man im Prinzip so viele Punkte zeichnen, wie man möchte – ob das jetzt zwei sind, oder 10, oder 100, wäre ganz dem Zeichner überlassen.











Kommentare (26)