Da fällt mir ein: Mathematische Bäume haben tatsächlich eine Gemeinsamkeit mit den Bäumen in der Natur. – Nein, es gibt keine Nationalparks, in denen wir sie nicht anrühren dürfen. (Wäre auch sinnlos: Wenn wir einen mathematischen Baum „fällen“, könnten wir ihn mit Zettel und Stift wieder zum Leben erwecken.) Die Gemeinsamkeit ist, dass mathematische Bäume auch Blätter tragen. So werden Punkte genannt, die mit nur einem anderen Punkt verbunden sind.
Zum Abschluss muss noch geklärt werden, was nicht-isomorph heißt. Am besten kann man das anhand von Baum a und Baum b erklären: Wenn ich das äußerst rechte Blatt von Baum b in Pfeilrichtung verbiege, sieht Baum b exakt gleich aus wie Baum a (man sagt: sie haben dieselbe Struktur). Dabei wird deutlich: Man kann aus einem Baum viele unterschiedliche Bäume erzeugen, indem man etwa einzelne Striche streckt oder verdreht, den ganzen Baum spiegelt oder kippt, etc. Alle Bäume, die auf diese Weise entstehen können, nennt man isomorph. Weil im Rätsel aber ausdrücklich nicht-isomorphe Bäume gefordert werden, bedeutet das, dass immer nur ein Baum (stellvertretend für all seine isomorphen Kollegen) gezählt wird. Baum a und Baum b würden im Rätsel quasi auch nur als ein einziger Baum gelten.
Bevor wir gleich loslegen, noch einmal die Regeln im Überblick:
– Der Graph darf keine Kreise enthalten.
– Es müssen 10 Punkte verwendet werden.
– Ein Punkt darf nicht mit genau zwei anderen Punkten verbunden sein.
– Zwei Bäume dürfen nicht isomorph sein.
Eine Frage bleibt uns aber noch: Wie gehen wir die Suche am geschicktesten an? Wenn wir uns in diesem förmlichen Wald von Bäumen zurechtfinden wollen, brauchen wir auf jeden Fall eine zuverlässige Landkarte, die uns zum Ziel führt. Ich habe mir dazu Folgendes überlegt:
Als erstes werden wir immer eine Kette bilden. Erst besteht sie nur aus einem Punkt (ist dann eigentlich keine Kette, aber egal), dann aus zwei Punkten, dann aus dreien, und immer so weiter. Sie wird quasi der „Stamm“ unseres Baumes sein. Die restlichen Punkte verteilen wir dann als Blätter auf jene Stammpunkte.
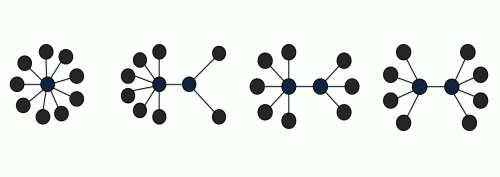
Beginnen wir mit dem einfachsten Baum: Wie sieht der aus? – Ganz einfach: Ein Punkt kommt in die Mitte (die berüchtigte Ein-Punkt-Kette), die verbleibenden neun hängen wir als Blätter an. So haben wir schon unseren ersten Baum, beziehungsweise unsere erste Schneeflocke (zumindest erinnert mich dieser Baum immer an eine).
Als nächstes ist der Stamm eine Zweierkette, die restlichen acht Punkte werden wieder verteilt. Eine kurze Zwischenfrage: Wie viele Blätter müssen wir jedem dieser Punkte mindestens zuordnen? – Zwei! Eines alleine würde nicht reichen – dann wäre der Punkt nämlich mit genau zwei anderen Punkten verbunden (dem Blatt und dem anderen Punkt). Das ist aber verboten! Welche Möglichkeiten haben wir also zur Verteilung der Blätter? – 6 und 2 … 5 und 3 … 4 und 4. Jetzt aber Achtung: „3 und 5“ ist dasselbe wie „5 und 3“, nur ist der Baum (um 180°) verdreht. Deswegen zählen sie nur als ein Baum – das Gleiche gilt auch für „2 und 6“ und „6 und 2“. Das führt uns zu unseren ersten vier Bäumen. Spoiler-Alarm: Gleich ist Halbzeit.
Wie geht es jetzt weiter? – Genau: Eine Dreierkette als Stamm, sieben Blätter müssen verteilt werden. Aber bevor wir uns die Mühe machen und alle möglichen Kombinationen einzeln durchgehen (4 und 1 und 2 … 3 und 2 und 2 … etc.), wenden wir einen kleinen Trick an: Dem mittlere Stammpunkt geben wir seine Blätter zuerst. Wir beginnen mit einem Blatt, dann bekommt er zwei, dann drei, und so weiter. Dass Außenpunkte mindestens zwei Blätter brauchen, haben wir vorher schon erkannt. Wie sieht es mit dem mittleren Punkt aus? – Na ja, eines braucht er unbedingt, ansonsten würde er gegen die 2-Verbindungen-Regel verstoßen (die benachbarten Stammpunkte). Weil dieses eine Blatt aber schon reichen würde, können wir folgern: Er braucht mindestens ein Blatt. Das bekommt er – es bleiben sechs Blätter für die äußeren Stammpunkte. Mögliche Aufteilungen: 4 (und 1) und 2 … 3 (und 1) und 3. Nun geben wir dem mittleren Stammpunkt zwei Blätter. Wie verteilen wir die restlichen? – 3 (und 2) und 2. Mehr Möglichkeiten haben wir gar nicht. Als nächstes drei Blätter in die Mitte. – Wieder gibt es nur eine Möglichkeit: 2 (und 3) und 2.











Kommentare (26)