Können wir vier Blätter in die Mitte geben? Dann würden immerhin noch drei Blätter für die Außenpunkte übrig bleiben. Aber wir wissen, dass jeder Außenpunkt zwei Blätter benötigt – mindestens! Das geht sich nicht aus – wir können also nicht mehr drei Blätter an den mittleren Stammpunkt hängen.
Würden wir jetzt fortfahren, dann würde uns ein Baum mit Dreierkette entgehen! Wie kann das denn sein? Sehen wir uns noch einmal den vorigen Baum (Verteilung 2 und 3 und 2) an: Die 3 Punkte am mittleren Stammpunkt verwenden wir allesamt als Blätter. Es spräche aber nichts dagegen, nur einen der Punkte direkt an den Stammpunkt anzuschließen (im Bild unten habe ich ihn grau dargestellt) und ihm dann die zwei bleibenden Blätter anzuhängen. Auf diese Weise erhalten wir schließlich unseren neunten (zugegeben recht schwierig zu findenden) Baum.
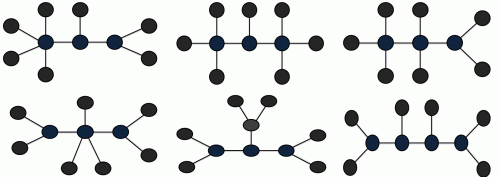
Keine Frage, wie es jetzt weitergeht: Eine Viererkette bildet den Stamm, daher gibt es diesmal zwei äußere und zwei innere Stammpunkte. Da jeder äußere Stammpunkt mindestens zwei Blätter benötigt und jeder innere mindestens einen, geht es sich exakt aus mit unseren sechs Blättern. Es gibt also nur eine Möglichkeit – (2 und 1 und 1 und 2) – und die ist nicht wirklich verzwickt zu finden. Damit sind es schon 10 Bäume:
Was passiert, wenn unsere Stammkette aus noch mehr als nur vier Punkten besteht? Probieren wir es einfach einmal mit fünf aus: In dem Fall gibt es zwei äußere und drei innere Stammpunkte, was bedeutet: Wir benötigen sieben Blätter. Die haben wir aber nicht – uns bleiben ja nur mehr fünf Stück übrig. Mit noch längeren Stammketten brauchen wir es dann gar nicht erst versuchen: Es bleibt also bei unseren 10 nicht-isomorphen, homöomorph irreduziblen Bäumen vom Grad 10. (Anmerkung: Es ist Zufall, dass es genau 10 Bäume vom Grad 10 gibt. Es existieren beispielsweise 5 solche Bäume vom Grad 9 und 14 Bäume vom Grad 11.)
Bleiben wir aber realistisch: Echte MIT-Professoren hätten dieses Rätsel mit Sicherheit noch schneller gelöst als wir gerade eben. Daniel Kleitman, der mathematische Berater des Films, hat sich da offensichtlich einen Spaß mit seinem Publikum erlaubt. Die Figuren, die Will an die Tafel kritzelt, wirken eindrucksvoll und komplex und lassen das Publikum darum an den teuflischen Schwierigkeitsgrad der Aufgabe glauben.
Uns wird also ein leichtes Rätsel als äußerst schwer verkauft. Aber mal ehrlich: Es war die einzige Möglichkeit! Wie viele mathematische Rätsel gibt es denn, an denen MIT-Professoren zwei Jahre lang zu knabbern hätten, die sich aber recht anschaulich auf einer Gangtafel lösen lassen? Wenn es überhaupt solche Rätsel gibt – ich bezweifle es – dann sind sie unglaublich schwer zu finden.
Jedenfalls ist es ein hochinteressantes Thema, das uns „Good Will Hunting“ näherbringt. Einerseits haben wir so die Graphentheorie kennengelernt – ein Teilgebiet der Mathematik, dem wir jeden Tag begegnen, auch wenn wir es nicht unbedingt merken: Jede Straßenkarte, jeder U-Bahn-Plan basiert auf den Ideen, die Leonard Euler schon vor rund 300 Jahren hatte. Und andererseits haben wir dieses Rätsel gelöst – ein Rätsel für Jedermann und für überall, wo man Zettel und Stift zur Hand hat. Einem Phänomen, das in der Mathematik generell häufig ist, begegnet man auch hier: Nur weil etwas wahnsinnig kompliziert klingt, heißt das nicht, dass es sich nicht doch als einfach herausstellen kann.
Wen jetzt jedenfalls die Begeisterung übermannt hat, kann die nächsten Hürden auf sich nehmen: Grad 11, Grad 12, etc. Wer aber die infernale Herausforderung sucht, kann sich dem Grad 3 widmen. Warum? – Sehen Sie selbst!











Kommentare (26)