Ich werde oft um Rat gefragt, wenn es darum geht, ein passendes Teleskop zu kaufen. Leider kann ich da wenig weiterhelfen. Ich bin zwar Astronom, aber war selbst nie ein Hobby-Astronom und habe auch nie selbst ein Teleskop besessen. Meine berufliche Erfahrung mit der beobachtenden Astronomie beschränkt sich auf die Arbeit mit professionellen Großteleskopen an Sternwarten und da laufen die Dinge ganz anders, als bei der privaten Hobby-Astronomie. Außerdem ist es enorm schwierig, allgemeine Hinweise zum Teleskop-Kauf zu geben. Es kommt dabei sehr stark darauf an, wie viel Geld man ausgeben will; was man beobachten möchte; wo man beobachten möchte; ob man mobil bleiben oder sich eine eigene kleine Sternwarte einrichten will – und so weiter. Ich verweise daher meistens immer auf eine ausführliche und persönliche Beratung im Fachhandel. Damit man sich aber trotzdem voran schon ein wenig informieren kann, hat Blog-Leser Alderamin netterweise eine sehr ausführlichen Gastbeitrag in fünf Teilen verfasst, der in den nächsten Tagen hier im Blog veröffentlicht wird. Gestern gab es den ersten Teil, heute geht es weiter mit Teil 2.
————————————————————–
Mein erstes Teleskop – Teil 2
Nachdem wir im Teil 1 erfahren haben, was das Amateurteleskop zeigt bzw. nicht zeigt, nun ein paar theoretische Grundlagen, um zu verstehen, was die Leistung des Teleskops bestimmt.
Leistungsparameter – worauf kommt es an?
Billige Kaufhausteleskope prahlen oft mit ihrer Vergrößerung. Die Vergrößerung alleine sagt aber gar nichts über die Qualität des Teleskops aus, man kann sie beliebig hoch treiben, wird in kleinen Teleskopen dann allerdings nicht viel sehen, und ohnehin gilt ob der zuvor genannten Mannigfaltigkeit der Himmelsobjekte nicht, dass mehr Vergrößerung immer besser sein muss, im Gegenteil. Lichtschwache Objekte erfordern geringere Vergrößerungen als Planeten oder der Mond, und manche Sternhaufen sind so groß, dass sie ein großes Blickfeld benötigen.

Die drei wichtigsten Leistungsparameter eines Teleskops: 1. Öffnung, 2. Öffnung, 3. Öffnung. (Bild: https://paine1776.wikispaces.com, CC-BY-SA 3.0)
Der wichtigste Leistungsparameter eines Teleskops ist seine Öffnung, d.h. der Durchmesser des Objektivs, das ist die vordere, große Linse (oder der große Spiegel beim Spiegelteleskop). Je größer das Objektiv, desto mehr Licht sammelt das Teleskop, umso lichtschwächere Objekte kann man erkennen. Die Lichtstärke des Teleskops wird als Grenzgröße angegeben, womit die theoretisch schwächste Größenklasse eines gerade noch zu erkennenden Sterns gemeint ist. Größenklassen von Sternen sind mit dem Faktor 100,4 = 2,512… gestaffelt. Das ist die fünfte Wurzel aus 100: fünf Größenklassen Helligkeitsunterschied bedeuten einen Faktor von exakt 105•0,4 = 102 = 100. Ein kleinerer Wert für die Größenklasse bedeutet hierbei eine größere Helligkeit. Die hellsten Fixsterne (Wega, Capella, Arktur) haben 0. Größe (auch 0m geschrieben (m für Magnitude), Sirius die negative Größe -1,6m, die Sterne des Orions etwa 1m, die des Großen Wagens 2m und die schwächsten mit bloßem Auge noch sichtbaren haben ca. 6m. Auf diese Grenzgröße des bloßen Auges und einen theoretischen dunkeladaptierten Pupillendurchmesser von 7 mm ist die Grenzgröße des Teleskops bezogen. Ein Teleskop hat eine Grenzgröße von
Grenzgröße = 2,5m • log10 ( (Öffnung [mm] / 7 mm) 2) + 6m
= 2,5m • 2 log10 (Öffnung [mm] / 7 mm) + 6m
= 5m • log10 (Öffnung [mm] / 7 mm) + 6m
Denn es sammelt das (Öffnung/7 mm) 2-fache an Licht im Vergleich zum bloßen Auge. Dieser Faktor umgerechnet in Größenklassen ergibt den Gewinn, der gegenüber der mit bloßem Auge erreichten 6. Größe erzielt werden kann.
Gleichzeitig bestimmt der Durchmesser das Auflösungsvermögen des Teleskops. Die begrenzte Öffnung des Teleskops (auch wenn sie sehr groß erscheint) wirkt wie ein optischer Spalt, der für eine punktförmige Lichtquelle eine Beugungsfigur verursacht, eine kleine Scheibe im Zentrum, umgeben von konzentrischen Ringen. Man sieht sie bei sehr hoher Vergrößerung von Sternen. Jeder Bildpunkt eines Objekts erzeugt ein solches Beugungsbild und diese überlappen sich bei flächigen Objekten wie Mond oder Planeten und verursachen eine Bildunschärfe.
Je mehr Öffnung, desto kleiner wird diese Beugungsfigur und desto schärfer wird das Bild. Das Auflösungsvermögen wird in Bogensekunden [“] gemessen. Eine Bogensekunde ist der 3600. Teil eines Winkelgrads und ungefähr 1/1800 des Monddurchmessers. Das Auflösungsvermögen gibt an, wie nahe zwei Punkte (etwa zwei Komponenten eines Doppelsterns) beieinander stehen dürfen, damit sie gerade noch im Teleskop getrennt werden können (in etwa der Abstand zwischen dem Zentrum der Beugungsfigur und dem ersten Ring). Die Auflösung eines Teleskops von 10 cm Durchmesser beträgt für grünes Licht der Wellenlänge 550 nm etwa 1,4″, eines von 20 cm hat ein doppelt so hohes Auflösungsvermögen von 0,7”. Es gilt also vereinfacht:
Auflösungsvermögen = 1,4″ • 100 mm / Öffnung [mm]
Zum Vergleich: Der Winkeldurchmesser des Mars in Erdnähe (Opposition) schwankt zwischen 14″ und 25″ (diese Variationsbreite ergibt sich durch die elliptische Bahn des Mars und der somit schwankenden Entfernung bei der größten Annäherung an die Erde). Viel weniger als 1″ Auflösung braucht es visuell jedoch nicht, da die Luftunruhe der Atmosphäre (im Fachjargon Seeing) meistens die praktisch erreichbare Auflösung auf 1″ oder schlechter begrenzt (lediglich beim „Lucky Imaging” kommt man näher an das theoretische Limit des Teleskops heran).
Das Auflösungsvermögen begrenzt auch die einsetzbare Vergrößerung, oberhalb der man lediglich ein unscharfes Bild größer und lichtschwächer macht, aber nichts gewinnt. Man möchte also möglichst viel Öffnung haben. Viele Amateure leiden an einer stark ansteckenden Krankheit, dem „Öffnungsfieber”, das sie nach immer größeren Teleskopen streben lässt. Unglücklicherweise steigt mit zunehmender Öffnung sowohl der Preis als auch das Gewicht des Teleskops überproportional an. Beides sind jedoch gute Gegenmittel gegen galoppierendes Öffnungsfieber.
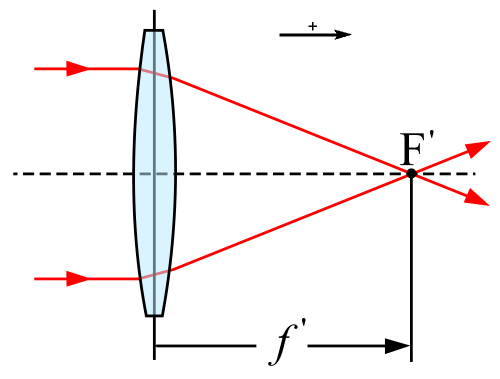
Brennweite einer Sammellinse: Der Punkt F’, in dem parallel durch die Linse einfallende Strahlen sich schneiden, heißt Brennpunkt der Linse, seine Entfernung f’ von der Linse heißt Brennweite (Bild: JiPaul / from Henrik, CC-BY-SA 3.0)
Der zweite wichtige Parameter ist die Brennweite des Teleskops (hierbei wird die Brennweite des Objektivs angegeben), sie ergibt die mit einem bestimmten Okular (so nennt sich die Linsengruppe auf der Augenseite des Teleskops; davon hat man stets mehrere verschiedener Brennweiten für verschiedene Vergrößerungen) erzielte Vergrößerung des Teleskops. Die Vergrößerung berechnet sich nach der einfachen Formel:
Vergrößerung = Objektivbrennweite / Okularbrennweite
Ein Okular mit 10 mm Brennweite liefert an einem Teleskop mit 1000 mm Brennweite also 100-fache Vergrößerung, an einem Teleskop mit 2000 mm Brennweite 200-fache.
Nur beim fotografischen Einsatz (den wir hier nur am Rande erwähnen wollen) bestimmt die Brennweite die Abbildungsgröße des Teleskops und zusammen mit seiner Öffnung die Lichtstärke. Fotoamateure kennen diese als Blendenzahl, die beim Teleskop fest ist, das sogenannte Öffnungsverhältnis:
Öffnungsverhältnis = Objektivdurchmesser / Brennweite = 1/Blendenzahl
Beispielsweise hat ein Teleskop mit 200 mm Öffnung und 1 m Brennweite ein Öffnungsverhältnis von 1/5 (häufig f/5 geschrieben, wobei f für „focal length” = Brennweite steht), entsprechend der fotografischen Blendenzahl 5, im Gegensatz zu einem Teleskop gleicher Öffnung mit 2 m Brennweite und Öffnungsverhältnis 1/10 (Blendenzahl 10). Fotografen wissen, dass Blende 10 die vierfache Belichtungszeit benötigt als Blende 5, weswegen man bei großem Öffnungsverhältnis auch von einem „schnellen” Teleskop spricht, bei einem geringen Öffnungsverhältnis von einem „langsamen”.
Wer das Teleskop hauptsächlich mit dem bloßen Auge benutzt, für den spielt das Öffnungsverhältnis und damit die Brennweite nur insofern eine Rolle, als dass sie die Baulänge des Teleskops beeinflusst, so wie die Kosten für die Okulare für die geringsten Vergrößerungen, da Okulare mit großen Brennweiten teuerer sind als solche mit geringen. Also will man stets die kürzeste Brennweite? Nein, leider zeigen schnelle Teleskope die stärksten Bildfehler (Randunschärfen, Farbsäume), deren Korrektur sie dann wieder verteuert. Eine große Brennweite macht das Teleskop hingegen schwer und teuer zu montieren. Hier ist ein guter Kompromiss gefragt.
Die zu wählenden Okularbrennweiten und damit Vergrößerungen richten sich nach dem Auflösungsvermögen des Teleskops. Generell gilt die Faustregel, dass die optimale Vergrößerung für eine bestimmte Öffnung des Teleskops etwa seinem Durchmesser in Millimetern entspricht. Bei kontrastreichen Objekten und ruhiger Luft darf man diesen Wert ruhig um das Doppelte überschreiten. So liefert ein Teleskop mit 20 cm Öffnung eine optimale Vergrößerung von 200fach, die etwa beim Mond, den Saturnringen oder engen Doppelsternen auch mal auf 400fach gesteigert werden darf.
Die lichtstärkste Vergrößerung erreicht man dann, wenn das verfügbare Licht auf einen möglichst kleinen Bereich der Netzhaut abgebildet wird, also bei einer möglichst geringen Vergrößerung, die auch das größte Blickfeld liefert. Hier gibt es jedoch eine praktische Grenze, die Größe der Austrittspupille des Okulars. Die Austrittspupille ist der helle Fleck im Okular, den man mit etwas Abstand vom Okular sieht und durch den das Licht des Teleskops austritt. Sie ist die Abbildung des Objektivdurchmessers im Okular. Ihr Durchmesser berechnet sich zu
Austrittspupille = Objektivdurchmesser / Vergrößerung
Die Austrittspupille wächst also mit zunehmender Öffnung und abnehmender Vergrößerung. Wenn sie größer wird, als die Augenpupille, dann fällt Licht außerhalb der Augenpupille, das somit verloren geht. Man erzielt also den maximalen Gewinn, wenn man die geringste Vergrößerung so wählt, dass ihre Austrittspupille am jeweiligen Teleskop der im Dunklen erweiterten Augenpupille entspricht, welche bei jungen Menschen bis 7 mm groß sein kann, im allgemeinen jedoch eher bei 5-6 mm liegt. Bei einem 20 cm durchmessenden Fernrohr kommt man bei 5 mm Austrittspupille auf 40-fache Vergrößerung als untere Grenze.

Austrittspupille bei einem Feldstecher (hier: 30 mm/8 = 3,75 mm) (Bild: Evan Mason, CC-BY-SA 3.0)
Die Vergrößerung bestimmt schließlich zusammen mit dem scheinbaren Gesichtsfeld des Okulars das wahre Gesichtsfeld des Teleskops. Es gibt Okulare mit verschiedensten scheinbaren Gesichtsfeldern, also dem Winkel des im Okular sichtbaren Blickfelds; dies ist ein Parameter, der nur durch das Okular bestimmt ist. Es gibt mittlerweile Okulare mit 110° scheinbarem Gesichtsfeld, bei denen man Kopf und Augen rollen muss, um den Rand des Gesichtsfelds zu sehen, man hat da schon den Eindruck, aus einem Fenster zu blicken. Diese kosten allerdings ein Vermögen und sind eher nicht die Wahl für Anfänger (wohl aber später für den ambitionierten Amateur eine wundervolle Ergänzung). Die typischen Gesichtsfelder guter, aber kostengünstiger Okulare (orthoskopisch, Plössl oder Erfle) liegen zwischen 50° und 70°. Das wahre Gesichtsfeld eines Okulars berechnet sich näherungsweise (für kleine scheinbare Gesichtsfelder) zu
Wahres Gesichtsfeld [°] = scheinbares Gesichtsfeld [°] / Vergrößerung
d.h. mit zunehmender Vergrößerung nimmt das Gesichtsfeld ab.
Zuletzt noch eine Anmerkung zum Okularsteckmaß. Es gibt Okulare mit 2 Zoll und 1,25 Zoll Durchmesser (von weniger wollen wir hier gar nicht erst reden…). Gute Teleskope können Okulare beiderlei Maßes verwenden, sie haben einen Anschluss für 2 Zoll mit einem herausnehmbaren Reduzierring auf 1,25 Zoll. Der Grund für die Einführung von 2-Zoll-Okularen lag darin, dass Okulare großer Brennweite mit großem Blickfeld ein Gesichtsfeld in der Brennebene des Teleskops überblicken, welches das 1,25-Zoll-Maß sprengt – das erfassbare Bild ist größer als 1,25 Zoll und passt nicht in dieses Steckmaß. Außerdem haben Spiegelreflexkameras im alten Normalformat 24×36 mm eine Bilddiagonale von 43 mm, das sind 1,7 Zoll. Damit die Bildränder voll ausgeleuchtet werden, muss ein entsprechend großer Teleskopanschluss gewählt werden. 2 Zoll leuchten ein solches Bild voll aus.











Kommentare (17)