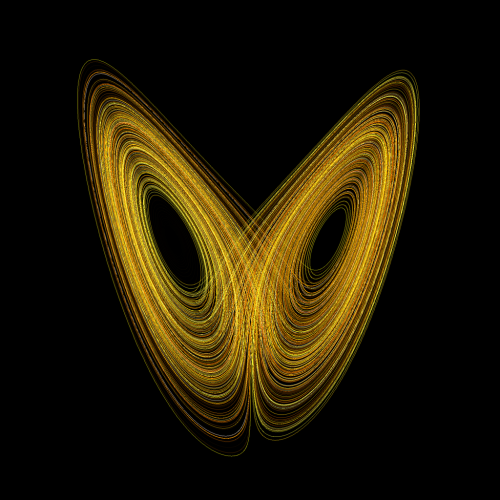
Es mag zwar so aussehen, als würden sich die Linien hier schneiden, aber das liegt eben daran, dass es nur ein zweidimensionales Bild eines dreidimensionalen Raums ist! Die Trajektorie des Lorenzattraktors trifft niemals auf sich selbst. Aber sie kommt sich selbst auch beliebig nahe. Es ist wirklich schwer vorstellbar, wie dieser Attraktor tatsächlich aussieht. Die Linie im Bild ist ja auch nicht der Attraktor selbst, sondern nur ein Phasenraumorbit, der vom Attraktor eingefangen wird. So wie sich eine Trajektorie bei der Pendeluhr immer der geschlossenen Kurve folgt, die das regelmäßige “Tick-Tack” der Uhr repräsentiert, folgt die Linie im Bild der komplexen Struktur des Lorenz-Attraktors. Einer Struktur, die sich mit normaler Geometrie nicht beschreiben lässt… Ein seltsamer Attraktor ist nicht einfach ein Punkt (oder eine Menge von Punkten) oder eine Linie oder eine Fläche. Er ist irgendwas dazwischen, ein Objekt mit einer sogenannten fraktalen Dimension (was das ist, habe ich hier ausführlich beschrieben). Also ein Objekt, das nicht eindimensional wie ein Linie, zweidimensional wie eine Fläche oder dreidimensional wie ein ausgedehnter Körper ist, sondern irgendwas dazwischen. Ein seltsamer Attraktor kann zum Beispiel “flächiger” als eine Linie sein aber immer noch weniger “flächig” als eine echte Fläche und eine Dimension besitzen, die irgendwo zwischen den Zahlen “1” und “2” liegt. Der Lorenz-Attraktor ist nur ein klein wenig fraktal; seine Dimension liegt bei etwa 2,05. Wäre er eine einfache zweidimensionale Fläche im dreidimensionalen Phasenraum, dann wäre er auch zweidimensional. Aber der seltsame Attraktor ist quasi so sehr in sich selbst verdreht, gefaltet und verschachtelt, dass er mehr ist als eine simple Fläche aber immer noch weniger als ein dreidimensionaler Körper.
Mathematisch kann man den seltsamen Attraktor als ein Objekt beschreiben, dass aus einem “normalen” Objekt entsteht, wenn man es immer wieder streckt, verdreht und auf sich selbst zurück faltet. Man kann sich vorstellen, dass das die Dinge enorm komplex macht. Egal wie nahe beieinander zwei Punkte im Phasenraum (die zwei unterschiedliche Anfangszustände repräsentieren) liegen, die ganzen Verdrehungen und Windungen des seltsamen Attraktors sorgen dafür, dass sie am Ende völlig unterschiedliche Wege gehen werden. Das kann man im folgenden Video gut sehen. Die roten Punkte repräsentieren verschiedene, einander ähnliche Ausgangzustände des Systems. Verfolgt man die zukünftige Entwicklung der jeweiligen Systeme, dann folgen die Trajektorien alle dem Attraktor. Die roten Punkte bewegen sich also alle entlang der seltsamen Strukturen die wir im Bild vorhin gesehen haben. Aber jeder Punkt folgt sehr schnell einem völlig anderen Weg. Ein paar landen auf der linken Seite des Attraktors, ein paar auf der rechten und im Laufe der Zeit mischt sich alles komplett durch und die zuvor eng benachbarten Punkte sind am Ende über den ganzen Attraktor verteilt. Oder anders gesagt: Die Modellatmosphären zeigen alle völlig unterschiedliche Zustände, obwohl sie am Anfang alle sehr ähnlich waren:
Auf einem seltsamen Attraktor folgt ein Phasenraumorbit einer unendlich langen, sich nie wiederholenden Bahn. Egal wie lange man wartet: das System wird niemals einen Zustand erreichen, den es vorher schon hatte. Es wird aber unterwegs jedem früher eingenommen Zustand beliebig nahe kommen. Und egal wie klein die Unterschiede zwischen zwei Zuständen am Anfang sind: Am Ende werden sie so groß sein, dass keine Möglichkeit mehr besteht, vom Ende auf den Anfang schließen zu können.
Die seltsamen Attraktoren sind also wirklich seltsam. Und man findet sie nicht nur in Lorenz’ vereinfachten Wettermodell. Man findet sie überall. Egal, ob man die Bewegung von Sternen in Galaxien betrachtet, die Strömung einer Flüssigkeit oder von Wind über einen Flugzeugflügel, die Vermischung von Flüssigkeiten oder irgendein anderes dynamisches System: Wenn ein gewisser Grad an Komplexität überschritten wird, dann wird man auch einen seltsamen Attraktor finden. Und mit ihm das Chaos…











Kommentare (19)