In den letzten Wochen habe ich viel über das Chaos geschrieben und ein paar meiner Meinung nach sehr interessante Phänomene aus der Chaosforschung vorgestellt (seltsame Attraktoren, Periodenverdoppelung, chaotische Universalität, die Mandelbrot-Menge und Fraktale). Dabei ging es aber vor allem um abstrakte Phänomen (kein Wunder, die Chaostheorie ist ja eigentlich auch ein Spezialgebiet der Mathematik) und weniger um konkrete Anwendungen. Es ist daher an der Zeit, sich einmal anzusehen, wie das Chaos sich in unserer Welt ganz real auswirkt. Passenderweise haben italienische Astronomen kürzlich eine interessante Arbeit publiziert, in der es um genau solche Auswirkungen geht: Die chaotische Beeinflussung der Bahnen von Navigationssatelliten durch den Mond (“Chaos in navigation satellite orbits caused by the perturbed motion of the Moon”).
Konfiguration von Galileo-Navigationssatelliten (Bild: Lukas Rohr, CC-BY-SA 3.0)
Dass die Bewegung der Himmelskörper in unserem Sonnensystem von einer chaotischen Dynamik bestimmt wird, ist keine neue Erkenntnis. Spätestens seit Henri Poincaré im 19. Jahrhundert nachgewiesen hat (siehe dazu auch hier), dass es mathematisch unmöglich ist, die Bewegung der Planeten für alle Zeiten vorherzusagen, wissen wir, dass das Chaos eine wichtige Rolle spielt. Die Verteilung der Asteroiden im Sonnensystem wird durch chaotische Effekte bestimmt, genau so wie die Struktur der Saturnringe, die Rotation von Monden um ihre Achse oder die Bewegung der Planeten. All diese Phänomene und ihre Auswirkungen werden seit Jahrzehnten intensiv untersucht. Aber die Naturgesetze gelten für die künstlichen Himmelskörper genau so wie für die natürlichen Objekte. Und das Chaos muss auch berücksichtigt werden, wenn es um die Steuerung von Satelliten in einer Bahn um die Erde geht. Genau das haben Aaron Rosengren vom Institut für angewandte Physik in Florenz und seine Kollegen getan.
Es ging den Forschern dabei vor allem die Frage des Weltraummülls beziehungsweise um dessen Vermeidung. Denn immer zahlreicher werdenden Schrott im All irgendwie “einzusammeln” ist zu teuer und zu ineffektiv um als realistische Option zu gelten (im wesentlich müsste man für jedes einzelne Schrottteil eine eigene Räummission ins All starten und würde dabei zwangsweise mehr Müll erzeugen, als man einsammeln kann). Man muss sich vor allem darum kümmern, das kein neuer Schrott mehr entsteht – also ausgediente Satelliten gezielt zum Absturz bringen oder auf “Parkorbits” verfrachten, wo sie ein paar Jahrhunderte oder Jahrtausende lang niemanden stören. Aber was, wenn dieser “Satellitenfriedhof” nicht so stabil ist, wie man denkt? Wenn chaotische Effekte die Bahnen der geparkten Satelliten stören und sie wieder näher an die Erde bringen? Und andererseits: Könnte man alte Satelliten nicht auch gezielt in instabile Regionen steuern, so dass das Chaos für ihren Absturz und damit ihre Entsorgung sorgt? Um all das beantworten zu können, muss man zuerst einmal genau wissen, wo sich die chaotischen Regionen befinden, welche Bahnen davon betroffen und wie stark die Auswirkung des Chaos sind. Hier besteht bei den künstlichen Himmelskörpern noch Nachholbedarf und darum haben sich Rosengren und seine Kollege die Sache mal ein wenig genauer angesehen.
Das Chaos wird hier – so wie auch bei den natürlichen Objekten – durch sogenannte Resonanzen verursacht. Ich habe das Thema früher schon mal sehr ausführlich erklärt, darum jetzt nur so viel: Von einer Resonanz spricht man, wenn die Bewegung von zwei Objekten in einem ganzzahligen Verhältnis zueinander steht. Zum Beispiel, wenn ein Asteroid zwei Runden um die Sonne genau in der gleichen Zeit absolviert in der Jupiter eine Runde schafft. Dann können die gravtitiven Störungen zwischen Jupiter und dem Asteroid periodisch wirksam werden und sich immer weiter aufschaukeln. Die Bahn des Asteroiden wird dadurch verändert und instabil – das heißt, sie wird immer stärker elliptisch und kreuzt dadurch die Bahnen anderen Himmelskörper. Am Ende kommt es dann zu einer Kollision und der Asteroid wird zerstört (oder er fliegt aus dem Sonnensystem raus). Darum findet man ja im Asteroidengürtel (oder den Saturnringen) an bestimmten Positionen Lücken; das sind die Orte, an denen Resonanzen wirken.
Resonanzen wie die eben beschriebene nennt man “Resonanzen der mittleren Bewegung” (oder “mean-motion resonances”). “Bewegung” wird aber in diesem Zusammenhang etwas umfassender definiert. Es geht nicht nur um die Bewegung eines Himmelskörpers durch den Raum, sondern auch um die Veränderung seiner Bahn. Die Bahnen der Himmelskörper sind ja variabel; sie werden größer oder kleiner; mehr oder weniger elliptisch und drehen sich im Raum hin und her. Es kann nun auch passieren, dass die Geschwindigkeit, mit der sich zum Beispiel die Bahn eines Asteroiden dreht in einem ganzzahligen Verhältnis zur Drehgeschwindigkeit der Bahn eines Planeten stehen. Oder die Periode mit der eine Bahn hin und her wackelt steht in einem ganzzahligen Verhältnis zur Wackelei einer anderen Bahn. All diese Resonanzen nennt man “säkulare Resonanzen” und sie spielen eine wichtige Rolle, wenn es um die Dynamik von Satelliten geht.
Das Problem ist nun, dass es bei der Bewegung von künstlichen Himmelskörpern sehr viele solcher säkularer Resonanzen gibt. Welche davon wie stark wirksam werden, hängt von vielen Faktoren ab. Davon, wie nah oder weit man von der Erde entfernt ist zum Beispiel oder welche Zeitskalen man betrachtet. Manche säkularen Resonanzen hängen mit der Rotation der Erde zusammen und laufen daher mit Perioden von wenigen Tag ab; andere werden durch die Bewegung der Erde um die Sonne verursacht und dauern Jahre. Wieder andere hängen damit zusammen, wie sich die Bahn des Mondes verändert oder wie die Erdachse im Laufe der Zeit hin und her schwankt und wirken sich daher erst im Laufe von Jahrzehntausenden aus. Rosengren und seine Kollegen haben sich bei ihrer Analyse auf die Navigationssatelliten konzentriert. Die befinden sich einige zehntausend Kilometer von der Erde entfernt und haben unterschiedlich stark geneigte Umlaufbahnen, um die gesamte Erde im Blickfeld haben zu können. Diese verschiedenen Bahnneigungen machen sie zu einem guten Studienobjekt – und ihre technische Bedeutung zu einem wichtigen Anwendungsfall!
In ihrer Arbeit haben die Wissenschaftler außerdem nur die Störungen betrachtet, die vom Mond verursacht werden (bei den solaren Resonanzen sind die Zeitskalen so lang, dass man sie vorerst vernachlässigen kann). Ihre Arbeit war analytisch, das heißt sie haben nicht wie sonst meistens üblich, die Bewegung der Satelliten numerisch am Computer simuliert um herauszufinden, ob sie sich irgendwann chaotisch bewegen. Arbeiten dieser Art wurden in der Vergangenheit schon gemacht und sie haben gezeigt, dass es tatsächlich unter vielen unterschiedlichen Bedingungen zu instabilen Satellitenbahnen kommen kann. Rosengren und seine Kollegen wollten aber nicht nur wissen ob Chaos auftritt, sondern auch warum und dafür müssen sie die entsprechenden mathematischen Gleichungen genau betrachten und mathematisch lösen, anstatt sie am Computer nur näherungsweise zu simulieren. Dieses Arbeitsgebiet der Mathematik nennt sich “Störungsrechnung”, ist ziemlich knifflig und wer mehr darüber wissen will, soll sich am besten meine Artikelserie zu diesem Thema ansehen (Teil 1, Teil 2, Teil 3, Teil 4). Im Wesentlichen geht es darum, eine sogenannte “Störungsfunktion” aufzustellen, die alle möglichen säkularen Resonanzen mathematisch zusammenfasst und diese Funktion zu untersuchen. Wer gerne mal wissen möchte, wie so etwas aussieht – bitte sehr:
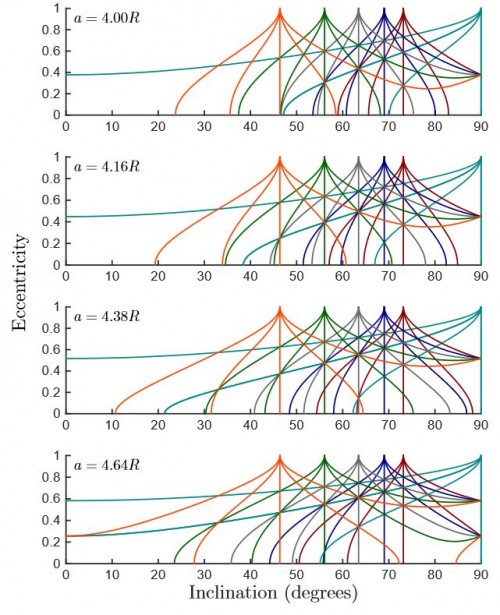
Ich werde das jetzt nicht im Detail erklären (das könnte ich auch gar nicht, ohne mich nochmal ein paar Wochen hinzusetzen und all das aufzufrischen, was ich damals im Studium gelernt habe). Am Ende geht es um zwei ganz bestimmte Größen: die “Länge des aufsteigenden Knotens” und das “Argument des Perihels”. Das sind zwei der sogenannten “Bahnelemente”, mit denen man die Bahn eines Himmelskörpers beschreiben kann. Knotenlänge und Argument des Perihels sind zwei der drei Winkel, die angeben, wie die Bahn im Raum orientiert ist und so wie alle anderen Bahnelemente verändern sie sich im Laufe der Zeit. Stehen nun die Änderungsraten von Knotenlänge/Argument des Perihels der Mond- bzw. Satellitenbahn in bestimmten ganzzahligen Verhältnissen, dann kommt es zu einer säkularen Resonanz und genau das war es, was Rosengren und seine Kollegen untersucht haben. Hier ist ein Beispiel für ihre Ergebnisse:
Die vier Diagramme zeigen die Parameter für vier verschiedene Navigationssatellitensysteme: GLONASS (Russland), GPS (USA), BeiDou (China) und Galileo (Europa). In jedem Bild zeigen die Achsen die Werte für die Bahnneigung und die Bahnexzentrizität an. Die bunten Linien sind die Positionen unterschiedlicher säkularer Resonanzen. Soll heißen: Ein Satellit, dessen Bahnneigung und Bahnexzentrizität Werte haben, die in dem Diagramm genau auf einer der bunten Linien liegen, wird von einer Resonanz beeinflusst. Auch ohne alle Details der Bilder zu verstehen, sieht man eines doch sehr deutlich: Es gibt viele Resonanzen, sie liegen einander oft sehr nahe und sie überlappen sich gegenseitig. Und damit ist man mitten im Chaos. Denn wenn sich ein Satellit in einer der Überlappungsregionen befindet, reichen oft schon kleine Veränderungen in der Bahn aus, um von einer Resonanz in die andere zu “springen” und damit die ganze Bahndynamik zu verändern (das ist genau das Verhalten, das ich auch schon bei der Betrachtung der seltsamen Attraktoren beschrieben habe.
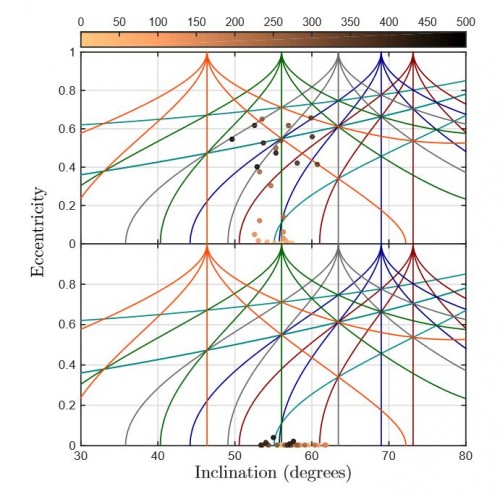
Rosengren und seine Kollegen haben das auch mit konkreten Beispielen illustriert. Das zeigt dieses Bild:
Hier sieht man die dynamische Entwicklung zweier fiktiver Galileo-Satillten im Verlauf von 500 Jahren. Die Bahnen der Satelliten sind anfangs identisch, nur ist eine Bahn um 120 Grad gegenüber der anderen gedreht (um die sogenannten Knotenlinie herum, also die Linie, die die beiden Schnittpunkte der Satellitenbahn mit der Ebene der Erdbahn verbindet). Die Diagramme sind identisch mit denen zuvor; nur sind diesmal Punkte eingetragen, die zeigen, wie sich Bahnneigung und Exzentrizität der Satelliten im Laufe der Zeit verändern. Die Farbe der Punkte gibt dabei den Zeitpunkt an (je heller, desto früher). Beim unteren Bild passiert nicht viel – die Bahn des Satelliten bleibt immer annähernd kreisförmig, das heißt seine Exzentrizität ist gleich Null und die Punkte landen alle auf der x-Achse. Beim oberen Bild sieht man aber gut, wie die Exzentrizität im Laufe der Zeit immer mehr anwächst und sich am Ende der 500 Jahre immer stärker ändert. Wenn die Bahn eines Satelliten aber zu sehr von der Kreisbahn abweicht, kommt er an seinem erdnächsten Punkt der Erde immer näher und damit auch der Atmosphäre, was schließlich durch die Reibung zu einem Absturz bzw. seiner Zerstörung sorgt.
Die Arbeit von Rosengren und seinen Kollegen zeigt also recht deutlich die Komplexität der chaotischen Dynamik auf. Nicht nur kommt es darauf an, ob man sich in einer Region befindet, in der Resonanzen wirksam sind bzw. sich überlappen oder nicht, sondern auch die ursprüngliche Konfiguration der Bahn spielt eine wichtige Rolle. Wie das eben so ist, wenn das Chaos eine Rolle spielt: Dann können schon kleinste Änderungen in den Anfangsbedingungen dramatische Auswirkungen haben. Die Drehung der Mondbahn im Laufe der Zeit – sie braucht knapp 19 Jahre für eine Drehung um die Knotenlinie – hat einen relevanten Einfluss auf die Stabilität von Satellitenbahnen und die Komplexität der säkularen Resonanzen ist der Grund, warum man bis jetzt Schwierigkeiten, eine stabile “Friedhofsregion” für die Galileo-Satelliten ausfindig zu machen. Rosengren und seine Kollegen wollen aber in zukünftigen Arbeiten genau dieses Chaos ausnutzen und zeigen, wie es für eine aktive Entfernung des Weltraumschrotts genutzt werden kann. Anstatt die ausgedienten Satelliten “sicher” zu parken, was angesichts der Resonanzen schwierig wird, sollen sie durch das Chaos gezielt abstürzen. Aber damit das klappt, muss man sich noch ein wenig intensiver mit der Identifizierung der Resonanzen beschäftigt. Davon gibt es erdnahen Weltraum noch jede Menge…

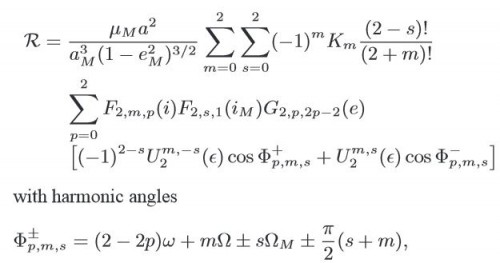










Kommentare (7)