Die Astronomen haben auch noch nach jeder Menge andere Resonanzen gesucht und einige (schwächere) gefunden. Insgesamt ergibt sich im Pluto-System also ein recht komplexes dynamisches Bild. Und immer da wo man komplexe Dynamik mit resonanter Bewegung vorfindet, muss man meistens auch nicht lange suchen, um irgendwo Chaos zu finden. Und das war auch bei Plutos Monden der Fall!
Es ist allerdings nicht so, dass die Bewegung der Monde um Pluto selbst chaotisch ist! Die Pressemitteilung der NASA zu diesem Thema ist da leider ein wenig missverständlich. Da wird zum Beispiel erzählt, man hätte einen “cosmic dance with a chaotic rhythm” bei den Monden gesehen. Und bei DRadioWissen (WebCite) hat man es sogar völlig falsch verstanden und schreibt unter der Schlagzeile “Pluto-Monde ein einziges Chaos”: “[Pluto hat seine Monde] offenbar nicht im Griff. Sie ändern ständig ihre Umlaufbahnen.”
Das ist natürlich Unsinn. Wären tatsächlich die Umlaufbahnen chaotisch, dann würde es die Monde längst nicht mehr geben. Auf chaotischen Bahnen die sich ständig verändern, wären die Monde schon lange miteinander kollidiert, mit Pluto zusammengestoßen oder ganz aus dem System geworfen worden. Ihre Bahnen sind resonant bzw. nahe einer Resonanz aber daraus folgt nicht zwingend, dass sie gleich komplett chaotisch sein müssen (Pluto selbst befindet sich zum Beispiel in einer Resonanz mit Neptun und kommt damit auch wunderbar klar).
Das Chaos um das es geht findet man bei der Eigenrotation der Monde Nix und Hydra. Normalerweise erfolgt diese Rotation auch bei Monden regelmäßig und meistens in Form der weiter oben schon erwähnten Spin-Resonanzen in Übereinstimmung mit der Umlaufperiode. Aber manchmal gibt es solche Regelmäßigkeiten nicht. Dann rotieren die Himmelskörper nicht schön regelmäßig um ihre eigene Achse, sondern “wackeln” oder “taumeln” ohne klare Periode hin und her. Ursache für dieses Verhalten sind dann meistens die gravitativen Störungen die durch verschiedene Resonanzen auftreten. Im Fall der Pluto-Monde wird das noch durch deren unregelmäßige Form verstärkt.
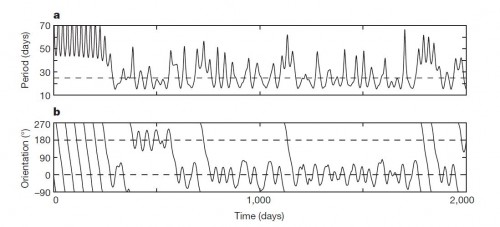
Dieses Bild aus der Arbeit von Showalter und Hamilton zeigt das Ergebnis einer Computersimulation zur Rotation von Nix. Oben sieht man, wie sich die Rotationsdauer von Nix während eines Zeitraums von 2000 Tagen ändert; unten sieht man, wie sich die Richtung der Rotationsachse verändert.
Wer sich an meine Serie über Chaostheorie erinnert, dem wird hier besonders das untere Diagramm auffallen. Hier sieht man, wie die Richtung der Rotationsachse zuerst einfach alle möglichen Werte zwischen 0 und 360 Grad einnimmt, bevor sie dann nach etwa 500 Tagen anfängt, um eine Richtung von 180 Grad zu schwanken. Später wechseln dann kurz Phasen mit Schwankungen zwischen 0 und 360 Grad mit kleineren Schwankungen um 0 Grad ab. Dieser Wechsel von einer “Zirkulation” zu einer “Libration” ist absolut typisch für chaotische Systeme!
Wäre Nix kein kleiner Mond, sondern ein großer Planet, dann könnte dieses Verhalten nicht unbedingt förderlich für die Entwicklung von etwaigem Leben sein. Denn wenn sich die Orientierung der Achse und die Dauer der Rotation (also die Dauer eines Tages) unvorhersagbar ändert, dann kriegt der Planet auch mal mehr und mal weniger Sonnenlicht ab; es wird sich kein stabiles mit stabilen Jahreszeiten herausbilden und welche Auswirkungen das auf die Entwicklung von höherem Leben hat, ist ungewiss. Auf jeden Fall wäre es verdammt knifflig, dort einen brauchbaren Kalender zu entwickeln!
Auf Plutos Monden Nix und Hydra ist jetzt wohl nicht mit Leben zu rechnen. Ihre chaotische Rotation ist aber trotzdem interessant. Einerseits, wenn es darum geht die Vergangenheit des Pluto-Systems und die Entstehung der Monde besser zu verstehen. Andererseits ist das Doppelsystem von Pluto und Charon mit seinen kleinen Monden ein tolles dynamisches Modell für ein Doppelsternsystem mit Planeten. Von denen gibt es ja jede Menge da draußen und wenn da die gleichen dynamischen Prozesse ablaufen wie bei Pluto, könnte man eventuell dort wirklich einen Planeten finden, dessen Rotation chaotisch abläuft.











Kommentare (18)