Verschlüsselung: Wie sie funktioniert und wie man sie anwendet

Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2015. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier. Informationen über die Autoren der Wettbewerbsbeiträge findet ihr jeweils am Ende der Artikel.

——————————————

Im letzten Jahr hat Dominic Wäsch auf Astrodicticum Simplex den Gastbeitrag Verschlüsselungsverfahren und ihre Sicherheit eingereicht. Darin beschreibt er unter anderem, was asymmetrische Verschlüsselungsverfahren sind: Jeder Teilnehmer hat einen geheimen und einen öffentlichen Schlüssel. Den geheimen Schlüssel behält man dabei für sich selbst, den öffentlichen dagegen kann man bedenkenlos veröffentlichen, etwa im Internet.

Wenn ich dir also eine Nachricht schicken möchte, verschlüssele ich sie mit deinem öffentlichen Schlüssel, und du kannst sie mit deinem geheimen Schlüssel entschlüsseln. Dabei kann man geheime Schlüssel nicht irgendwie aus öffentlichen ableiten, sodass wirklich nur derjenige mit dem geheimen Schlüssel die Nachricht lesen kann, also nur du. Ich kann die Nachricht zudem mit meinem geheimen Schlüssel signieren, das bedeutet, dass du sicher sein kannst, dass die Nachricht wirklich von mir kommt. Die Signatur kannst du dann mit meinem öffentlichen Schlüssel überprüfen.

Das alles klingt nach einer Menge Aufwand, weshalb ich bitten möchte, nicht sofort abzuschalten, auch wenn Wörter wie „Algorithmus“ vorkommen. Verschlüsselung ist wichtig, um unser aller Privatsphäre zu schützen, und sie ist heutzutage außerdem kinderleicht! Heutzutage hat sich der PGP-Standard etabliert, der dann von verschiedenen Programmen umgesetzt wird, üblicherweise ist das das Programm GPG. Bei GPG kann man sich aussuchen, welchen Verschlüsselungsalgorithmus man benutzen möchte, dabei ist der RSA-Algorithmus der üblichste.

Ich möchte im ersten Abschnitt beschreiben, wie der RSA-Algorithmus funktioniert. Für die darauf folgenden Teile, ist kein Verständnis von RSA erforderlich, jedoch ist der erste Teil der eigentlich wissenschaftlich interessante. Danach beschreibe ich, was es mit PGP und GPG auf sich hat und anschließend, wie man seinen Nachrichten konkret verschlüsseln und signieren kann.

Der RSA-Algorithmus

Das Originalpaper, auf dem dieser Abschnitt basiert, heißt A Method for Obtaining Digital Signatures and Public-Key Cryptosystems von Rivest, Shamir und Adleman.

Wir suchen uns zuerst zwei beliebige Primzahlen (Zahlen, die nur durch 1 und sich selbst teilbar sind) aus und nennen sie p und q. Sei also p = 3 und q = 11. Nun rechnen wir p*q und nennen das Ergebnis n, also n = p*q = 3*11 = 33. Nun benutzen wir die sogenannte „Eulersche Funktion“ φ (sprich: Vieh) und rechnen φ(n) (sprich: φ von n) aus.

Es geht über den Rahmen dieses Textes heraus zu erklären was die φ-Funktion macht, wir benutzen einfach mal zwei Regeln:

1. Wenn x und y Primzahlen sind, gilt φ(x*y) = φ(x) * φ(y).

2. Wenn x eine Primzahl ist, gilt φ(x) = x-1.

Wir haben also Glück und es gilt für uns φ(n) = φ(p) * φ(q) = (p-1) * (q-1) = (3-1) * (11-1) = 2*10 = 20.

Als nächstes suchen wir uns eine teilerfremde Zahl zu φ(n) aus, die größer als 1 und kleiner als φ(n) ist, und nennen sie e. Teilerfremd bedeutet, dass die Zahlen nicht durch die gleiche Zahl teilbar sein dürfen, außer natürlich durch 1. 12 und 15 wären zum Beispiel nicht teilerfremd, denn sie sind beide durch 3 teilbar. In unserem Fall setze ich e = 13, weil 13 und 20 teilerfremd ist.

Als nächstes benutzen wir ein Prinzip namens „Kongruenz“. Das Kongruenzzeichen ≡ ist ein Gleich-Zeichen mit drei Strichen. Man kann sagen: x ≡ y mod z, wenn x mod z = y mod z ist. Das „mod“ steht dabei für „Modulo“, was quasi beim Teilen mit Rest der Rest ist. Es gilt etwa: 7 mod 2 = 1, weil 7 / 2 = 3 Rest 1 ist. Bei Kongruenz gilt etwa: 2 ≡ 8 mod 6, weil 2 mod 6 = 8 mod 6 = 2 ist.

Wir können jetzt im Bezug auf die Kongruenz ein sogenanntes „multiplikativ Inverses“ bestimmen. Multiplikativ invers bedeutet: Wenn x*y ≡ 1 mod z gilt, dann sind (für mod z) x und y multiplikativ invers zueinander. Was wir nun brauchen, ist das multiplikativ Inverse zur Zahl e für mod φ(n); die Zahl nennen wir dann d. Dazu benutzen wir den erweiterten Euklidischen Algorithmus, der für unser Beispiel so geht: Zur Erinnerung: e = 13 und φ(n) = 20.

20 = 1*13 + 7 (I)

13 = 1*7 + 6 (II)

7 = 1*6 + 1 (III)

Wir stellen jetzt nach 1 um:

1 = 7-1*6 (Umgestellte Gleichung III)

1 = 7-(13-1*7) (Wir haben für 6 = 13-1*7 die umgestellte Gleichung II eingesetzt.)

1 = (20-1*13)-(13-1*(20-1*13)) (Wir haben für 7 = 20-1*13 die umgestellte Gleichung I eingesetzt.)

1 = 2*20 – 3*13

Da Gleichheit gilt, gilt auch Kongruenz:

1 ≡ 2*20 – 3*13 mod 20 (Wir streichen die 2*20, weil wir das bei mod 20 können.)

1 ≡ -3*13 mod 20 (Wir addieren 20 auf die -3)

1 ≡ (-3+20)*13 mod 20

1 ≡ 17*13 mod 20

Und tadaa, schon haben wir unser multiplikativ Inverses! Es gilt also d = 17. (Probe: 13*17 = 221. 221 mod 20 = 1. Stimmt also.)

Unser öffentlicher Schlüssel besteht nun aus den Zahlen e und n, also 13 und 33, während unser geheimer Schlüssel aus den Zahlen d und n, also 17 und 33 besteht. Alle anderen Zahlen brauchen wir jetzt nicht mehr.

Aber, wirst du jetzt sicher sagen, stopp: Das ist ja total unsicher, wenn ich glaube, dass man aus dem öffentlichen Schlüssel nicht den geheimen herausbekommen kann! Wer das Verfahren kennt, kann einfach das öffentliche n benutzen, um daraus das angeblich geheime d zu bekommen. In unserem Fall müsste man also aus der 33 die 17 ableiten, und das geht ja ganz einfach: Man muss nur φ(33) bilden und danach die oben beschriebenen Schritte durch gehen, und man hat den geheimen Schlüssel. Bei uns ist ja n = 33, also 3*11. Wir wenden die eine Regel mit den Primzahlen an und rechnen einfach: φ(33) = φ(3) * φ(11) = (3-1)*(11-1) = 2*10 = 20.

Die Lösung ist, und allein darauf basiert die Sicherheit von RSA, dass man φ(n) in der Praxis nur sehr schwer ausrechnen kann. Man benutzt einfach riesengroße Primzahlen. Primzahlen mit mehreren hundert Stellen. Die gibt es, und Computer können sie finden. Du suchst dir also zwei davon „zufällig“ heraus, rechnest die eine mal die andere und hast dann das Produkt, das wir n genannt haben. Um jetzt das φ(n) zu berechnen, muss ich aus dem n erst mal wieder die beiden Primzahlen herausbekommen, und das ist verdammt schwierig. Bei 33 geht das noch, da bekomme ich ganz leicht 3 und 11 heraus. Aber wenn das n sehr groß ist, kann ich das nicht, auch wenn ich ein Computer wäre. Es ist unter heutigen Bedingungen nicht möglich. Man kennt einfach kein schnelles Faktorisierungsverfahren für Produkte großer Primzahlen, und wenn die Mathematikergemeinde bis heute keines gefunden hat, kann man davon ausgehen, dass es ein schwieriges Problem ist, an dem man noch ziemlich lange arbeiten wird. Aber vielleicht wird morgen schon jemand drauf kommen und wir müssen uns einen besseren Algorithmus ausdenken.

Ein Problem für RSA stellen allerdings Quantencomputer dar. Man braucht kein effektives Verfahren, wenn man ausreichend leistungsstarke Computer hat. Falls es solche Computer gibt, hat aber nicht nur RSA ein Problem: Auch viele andere kryptographische Algorithmen basieren auf schwierigen mathematischen Problemen, die ebenfalls durch Quantencomputer gelöst werden können. Der Diffie-Hellman-Algorithmus basiert zum Beispiel auf dem Problem, dass man diskrete Logarithmen nicht (schnell) ausrechnen kann. Wir müssen also darauf hoffen, dass etwa die NSA keine entsprechenden Computer besitzt. Da allerdings selbst Edward Snowden zu dem Thema lediglich enthüllt hat, dass die NSA versucht, einen Quantencomputer zu bauen, halte ich RSA derzeit für sicher.

Kommen wir nun zum Benutzen des Schlüsselpaares. Wir wollen jetzt eine Botschaft b verschlüsseln und signieren, um sie hinterher wieder entschlüsseln und die Signatur zu überprüfen. Bei der Botschaft können wir irgendeine Zahl wählen, die kleiner als unser n = 33 ist. (Man kann selbstverständlich auch Buchstaben und Sonderzeichen verschlüsseln, dazu übersetzt man sie mit Codierungsverfahren wie ASCII oder UTF-8 in Zahlen) Ich suche mir also die Zahl b = 2 aus und kenne deinen öffentlichen Schlüssel (e, n) = (13, 33).

Ich generiere den Geheimtext g nun so:

g = b^e mod n (Wir setzen unsere Zahlen ein)

g = 2¹³ mod 33 (Ein Fall für den Taschenrechner)

g = 8

Die 8 schicke ich dir nun zu und du entschlüsselst sie mit deinem geheimen Schlüssel (d, n) = (17, 33).

b = g^d mod n

b = 8¹⁷ mod 33

b = 2

Und siehe da, die Botschaft wurde entschlüsselt! Jetzt kannst du mir eine andere Botschaft B = 3 zurückschicken. Um die Nachricht zu verschlüsseln, bräuchtest du meinen öffentlichen Schlüssel, das lassen wir mal einfachheitshalber mal weg. Stattdessen signierst du die Botschaft B mit deinem geheimen Schlüssel, sodass daraus die signierte Botschaft s wird, und das geht so:

s = B^d mod n

s = 3¹⁷ mod 33

s = 9

Nun kann ich überprüfen, ob die Nachricht auch wirklich von dir geschickt wurde, das überprüfe ich mit deinem öffentlichen Schlüssel:

B = s^e mod n

B = 9¹³ mod 33

B = 3

Es ist wieder unser B von oben herausgekommen, die Signatur wurde also verifiziert.

Aber warum funktioniert das? Wir können dazu den Satz von Euler benutzen (Wikipedia hat einen Beweis dazu) der folgendes aussagt:

Wenn x und y teilerfremd sind, gilt: x^φ(y) ≡ 1 mod y.

Bei RSA gilt ja anscheinend, dass b ≡ b^ed ≡ b^de (mod n) ist. (Also die Botschaft ist kongruent zur Entschlüsselung der Verschlüsselung der Botschaft, die kongruent zur Verifizierung der Signatur der Botschaft ist. Logisch.) Es gibt in der Mathematik ein paar sogenannte Potenzgesetze, eines davon ist: x^yz = x^{y * z}. Wenn wir das Potenzgesetz anwenden, ist klar, dass gilt: b^ed = b^de = b^{e * d}. Aber jetzt müssen wir noch zeigen, dass auch gilt: b^{e * d} ≡ b (mod n).

Praktischerweise wissen wir, dass e und d (für mod φ(n)) multiplikativ invers zueinander sind, deshalb gilt ja: e*d ≡ 1 mod φ(n). Das können wir umschreiben zu e*d = k*φ(n) + 1, wobei k irgendeine ganze Zahl ist. Es gilt also:

b^e*d ≡ b^{k*φ(n) + 1} mod n. Wir können die 1 aus dem Exponenten herausziehen, sodass sich ergibt:

b^e*d ≡ b * b^{k * φ(n)} mod n. Jetzt wenden wir unser Potenzgesetz „rückwärts“ an.

b^e*d ≡ b * b^φ(n)k mod n. So, und jetzt können wir endlich den Satz von Euler anwenden, der hier aussagt: b^φ(n) ≡ 1 mod n. Das dürfen wir, weil b kleiner ist als das n ist, das wir aus zwei großen Primzahlen zusammengesetzt haben. Solange b also nicht eine dieser Primzahlen ist, sind b und n teilerfremd und der Satz gilt, also:

b^e*d ≡ b * 1^k mod n. Da eins hoch irgendwas immer eins ist, bekommen wir das raus, was wir haben wollten:

b^e*d ≡ b mod n. Yay.

Wir wissen jetzt also, was der RSA-Algorithmus ist, wie er funktioniert. Jetzt wollen wir aber wissen, wie er zum Einsatz in der Software kommt.

PGP und GPG

In diesem Abschnitt geht es darum, was PGP und GPG sind und wie sie funktionieren. Wie man seine Nachrichten nun konkret verschlüsselt und signiert, ist in nächsten Abschnitt erklärt.

PGP steht für „Pretty good Privacy“, also „Ziemlich gute Privatsphäre“. PGP bezeichnete zuerst ein Programm, das 1991 von Philip Zimmermann geschrieben wurde. Zimmermann benutzte dabei in seinem Programm eine hybride Verschlüsselung, also eine Mischung aus symmetrischer und asymmetrischer Verschlüsselung. Ein symmetrisches Verfahren bedeutet, dass es den gleichen Schlüssel zum Ver- und Entschlüssen benutzt. Bei einem asymmetrischen Verfahren dagegen gibt es einen öffentlichen und einen geheimen Schlüssel, dabei wird der öffentliche Schlüssel zum Verschlüsseln und der geheime Schlüssel zum Entschlüsseln benutzt, wie etwa bei RSA.

Ein Beispiel für ein symmetrisches Verfahren ist die Caesar-Verschlüsselung. Bei Caesar „verschiebt“ man einfach die Buchstaben um den Schlüssel. Wenn der Schlüssel 5 ist, verschiebt man die Buchstaben um 5, und es ergibt sich:

a b c d e f g h i j k l m n o p q r s t u v w x y z
f g h i j k l m n o p q r s t u v w x y z a b c d e

Aus dem Wort „Hallo“ wird mit Caesar-5 also „Mfqqt“. Caesar hat also ein ziemlich unsicheres Verfahren benutzt, man muss ja nur 26 Möglichkeiten ausprobieren. Es gibt aber auch sicherere symmetrische Algorithmen, zum Beispiel den AES. Den AES möchte ich hier nicht erklären, wer daran interessiert ist, kann diesen Comic zum Thema lesen.

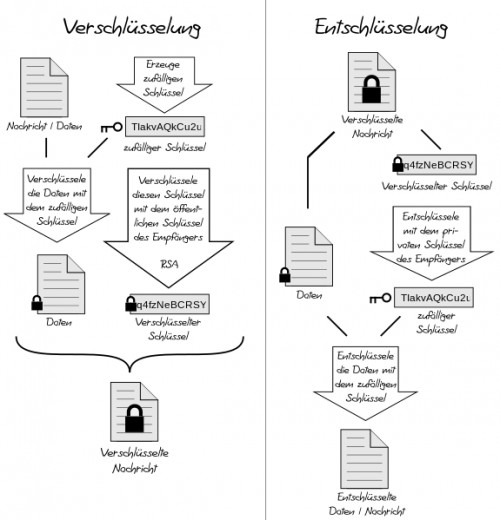
Wie funktioniert die hybride Verschlüsselung nun? Wir haben zuerst ein Dokument, das wir jetzt verschlüsseln wollen. Wir generieren uns nun einen zufälligen Schlüssel (S) für ein symmetrisches Verfahren und verschlüsseln damit die Nachricht. Dann nehmen wir den Schlüssel S und verschlüsseln ihn mit dem öffentlichen Schlüssel des Empfängers, den wir schon kennen. Der verschlüsselte Schlüssel S und die verschlüsselte Nachricht kann dann an den Empfänger übermittelt werden, der dann zuerst den Schlüssel S mit seinem geheimen Schlüssel entschlüsselt und die Nachricht dann mit dem nun entschlüsselten Schlüssel S entschlüsselt. Alles klar? Dieses Bild stellt das Verfahren gut dar:

Bild: Gregorerhardt, CC-BY-SA 4.0

Um PGP so transparent wie möglich zu machen, wurde der OpenPGP-Standard entwickelt, und jeder darf Programme schreiben, die diesen Standard umsetzen. Wenn man heutzutage PGP sagt, meint man dabei selten die von Zimmermann geschriebene Software, sondern meistens diesen Standard. Bestandteile dieses Schlüssels sind eine oder mehrere Benutzer-IDs. Diese bestehen normalerweise aus dem Vor- und Nachnamen des Schlüsselbesitzers und seiner E-Mail-Adresse. Wer mehr als eine E-Mail-Adresse hat, kann auch mehr als eine Benutzer-ID haben, man kann die E-Mail-Adresse aber auch weglassen. Man kann auch einen Kommentar angeben, das sollte man aber eigentlich nur machen, wenn man einen Allerweltsnamen hat, an dem man nicht identifiziert werden kann. Eine Benutzer-ID kann dann z.B. so aussehen: Hans Meyer (Astronom) <hans.meyer@scienceblogs.de>. Außerdem kann man aus dem Schlüssel erkennen, welcher Algorithmus zum Verschlüsseln und Signieren benutzt werden soll, und der Schlüssel enthält natürlich auch den eigentlichen Schlüssel, und eventuell Unterschlüssel, also die langen Zahlen, mit denen Texte ver- und entschlüsselt sowie signiert werden können. Es ist außerdem möglich, ein Bild von sich zu dem Schlüssel hinzuzufügen. Ein weiterer Teil des Schlüssels sind Signaturen Dritter, dazu komme später.

All diese Daten werden dann in einem bestimmten Verfahren, das hier beschrieben ist, in einen Haufen Zeichen umgewandelt. Mein öffentlicher Schlüssel sieht dann zum Beispiel so aus. Das sieht für das menschliche Auge ziemlich nichtssagend aus, man kann aus diesen Zeichen aber die oben genannten Informationen ableiten. Das muss man aber nicht selber irgendwie herausfinden, sondern man lässt das Programme machen. Die „verbale Interpretation“ meines öffentlichen Schlüssels kann man auch hier ansehen.

Die Seite, auf die ich gerade gelinkt habe, ist ein Keyserver, ein wichtiges Instrument zum Schlüsselaustausch. Auf einen solchen Server kann man seinen öffentlichen Schlüssel hochladen, damit man ihn öffentlich einsehen kann. Es gibt mehrere Keyserver weltweit, die ständig ihre Schlüssel synchronisieren, sodass alle auf dem neuesten Stand sind. Wenn du mir jetzt eine Nachricht senden möchtest, kannst du einfach auf einem beliebigen Schlüsselserver (z.B. sks-keyservers.net) meinen Namen suchen. Es kann nun aber sein, dass mehrere Schlüssel angezeigt werden. Woher weiß man jetzt, welcher davon der richtige ist?

Die Lösung für dieses Problem sind Signaturen. Aus jedem öffentlichen Schlüssel wird ein sogenannter Fingerabdruck erzeugt, an dem der Schlüssel eindeutig identifiziert werden kann. (Aus dem Fingerabdruck leitet sich dann auch die Schlüssel-ID ab, die die letzten 8 Zeichen des Fingerabdrucks ist.) Mein Fingerabdruck zum Beispiel ist 27E0 FC54 7163 DAA0 DFDA 9DA6 6E06 D478 B670 0FD9. Dieser Information solltest du jedoch nicht trauen, denn ich habe sie nicht besonders sicher geschickt. Florian könnte diesen Text zum Beispiel verändert haben. Hat er wahrscheinlich nicht, aber man sollte trotzdem dieser Information nicht sofort trauen. Wenn man nun aber persönlich jemanden trifft, der auch einen PGP-Schlüssel hat, kann man seine Fingerabdruck auf einem Stück Papier austauschen, und sich gegenseitig ausweisen, dass man wirklich der ist, der man vorgibt zu sein. Anschließend signiert man den Schlüssel, auf den der Fingerabdruck passt. Wie man das genau macht, hängt von Programm ab, das man benutzt. Jetzt schickt man den veränderten Schlüssel dem Besitzer zu, der ihn nun wieder auf den Schlüsselserver hochladen kann.

Als Resultat sieht man auf den Schlüsselservern, dass die Schlüssel signiert wurden. Hilfreich ist es, wenn zwei Leute einen gemeinsamen Bekannten haben: Man vertraut dem Schlüssel des gemeinsamen Bekannten, dann kann man auch allen Schlüsseln vertrauen, die der gemeinsame Bekannte unterschrieben hat. Dieses entstehende „Netz“ aus Signaturen nennt man auch das „Web of Trust“, das sind Schlüssel, die sich alle gegenseitig direkt oder indirekt vertrauen. Es ist wichtig, das Web of Trust zu stärken, indem man so viele Schlüssel signiert wie möglich (aber natürlich nur, nachdem man überprüft hat, ob sie dem Besitzer gehören). Diese Seite ist zum Beispiel ein Verzeichnis für alle Leute, die bereit sind, Schlüssel zu signieren. Man kann da nach der nächstgrößeren Stadt in seiner Umgebung suchen und entsprechende Leute finden. (Mich zum Beispiel findet man in Hannover.)

Wie man GPG benutzt

Ich habe ja schon gesagt, das der PGP-Standard von jedermann in einem Programm umgesetzt werden darf. Das Programm, dass die meisten dabei benutzen, heißt GPG, das steht für „GNU Privacy Guard“. GPG ist für alle mir bekannten Betriebssysteme verfügbar: Für Microsoft Windows gibt es Gpg4win, für Mac OS X gibt es die GPGTools und bei den meisten Linux-Distributionen ist GPG ohnehin schon als „gnupg“ oder „gnupg2“ vorinstalliert, aber falls nicht, gibt es hier eine Liste mit Installationsanweisungen. Viele E-Mail-Programme haben auch ein Plugin für GPG, für Thunderbird etwa ist das Enigmail.

Die oben verlinkten Programme haben fast alle eine graphische Oberfläche. (Die Ausnahme sind die Linux-Pakete, aber auch für die Linux-Distributionen gibt es meistens ein graphisches Programm.) Man kann sie eigentlich recht intuitiv bedienen, es gibt aber auch Tutorials im Internet (auch auf Deutsch: Enigmail, Gpg4win, GPGTools), die Restfragen klären können. Man kann GPG jedoch auch auf der Kommandozeile benutzen, und hier sehen die Befehle immer gleich aus. Ich möchte jetzt nur die häufigsten Befehle auflisten, ein ausführlicheres Tutorial für GPG auf der Kommandozeile gibt es hier.

• Schlüsselpaar erzeugen: gpg --gen-key. Man wird nun gefragt, welchen Algorithmus man benutzen will (RSA natürlich), wie lange der Schlüssel gültig sein soll, wie man heißt und welche E-Mail-Adresse benutzt werden soll. Die anschließende Schlüsselgenerierung kann dann ein bisschen Zeit kosten, das kommt bei RSA daher, dass zwei extrem große Primzahlen gesucht werden müssen. Wenn der Vorgang abgeschlossen ist, hat man einen privaten und einen öffentlichen Schlüssel.

• Öffentlichen Schlüssel veröffentlichen. Man kann den Schlüssel nun an einen Keyserver schicken, das geht so: gpg --send-key [Schlüssel-ID]. Man kann seinen Schlüssel aber auch in eine Datei schreiben, das geht so: gpg -a --export [Schlüssel-ID] > [Dateiname].

• Schlüssel importieren: Wenn jemand einem eine Datei mit einem Schlüssel gegeben hat, kann man den so importieren: gpg --import [Dateiname].

• Schlüssel empfangen: Man kann auf Schlüsselservern nach Namen suchen: gpg --search-keys [Name]. Wenn man schon die Schlüssel-ID des Schlüssels kennt, den man haben möchte, kann man sich den auch so herunterladen: gpg --recv-keys [Schlüssel-ID].

• Schlüssel anzeigen: Man kann sich jetzt alle Schlüssel, die man hat, mit gpg -k anzeigen lassen.

• Nachricht verschlüsseln und signieren: gpg -sear [Empfänger]. Das s steht dabei für das englische sign, e für encrypt, a dafür dass man das Ergebnis als ASCII-Text und nicht als Bytestrom haben will, und r für receiver. Man kann mit gpg -sa auch nur signieren, und mit gpg -ear nur verschlüsseln.

• Nachricht entschlüsseln: Das geht mit gpg -d für decrypt.

• Fingerabdruck anzeigen: Die Zeichenkette, die den Schlüssel eindeutig identifiziert: gpg --fingerprint [Name oder Schlüssel-ID]

• Schlüssel signieren: Wenn man geprüft hat, dass der Schlüssel echt ist, kann man ihn signieren: gpg --ask-cert-level --sign-key [Schlüssel-ID].

Denjenigen, die das Ver- und Entschlüsseln üben möchten, empfehle ich den Subreddit GPGpractise.

Ich hoffe, das ich euch die Prinzipien von RSA, PGP und GPG ein wenig näher bringen konnte, und vielleicht auch den einen oder anderen überzeugen konnte, seine Nachrichten zu verschlüsseln. Wenn ich sie beantworten kann, beantworte ich gern auch Fragen in den Kommentaren.

————————————————-
Hinweis zum Autor: Dieser Artikel wurde von Philip geschrieben.

Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2015. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier. Informationen über die Autoren der Wettbewerbsbeiträge...