Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2016. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier.

Das sagt der Autor des Artikels, kein Name über sich:
Ich habe Physik studiert, arbeite aber inzwischen in der Industrie. Meine Freude an der Wissenschaft habe ich aber nicht verloren und so gehe ich gerne in Vorträge oder lese in aktuellen Veröffentlichungen. Mein besonderes Interesse ist zur Zeit das menschliche Gehirn und warum wir ihm nicht immer trauen dürfen.
——————————————
Das Lesen von wissenschaftlichen Studien oder wie signifikant ist „Statistische Signifikanz“?
Ich finde, es lohnt sich, bei Artikeln zu wissenschaftlichen Erkenntnissen auch die Originalstudie zu lesen, besonders bei Klassikern oder bei Durchbrüchen in der Wissenschaft.
Für mich war dieses Jahr das bisherige Highlight dabei der direkte Nachweis von Gravitationswellen (und nicht nur, weil es beinahe an meinem Geburtstag veröffentlicht wurde):
Observation of Gravitational Waves from a Binary Black Hole Merger [1]
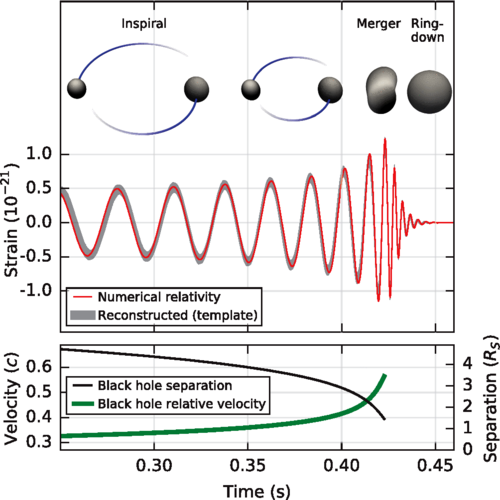
aus B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) Phys. Rev. Lett. 116, 061102 – Published 11 February 2016 Creative Commons Attribution 3.0 License
Abbildung 1: Verlauf der Verschmelzung zweier Schwarzer Löcher
Dabei gibt es ein paar Aspekte, die mir bei diesem Paper besonders gefallen. Das Paper
– ist für ein Thema an der Speerspitze der Forschung eigentlich sehr verständlich,
– zeigt kurz den Weg von der theoretischen Vorhersage über die
– ersten indirekten Nachweise im Doppelpulsar zum
– aktuellen Experiment,
– beschreibt das zugrunde liegende physikalische Phänomen und
– den verwendeten Versuchsaufbau.
Im Abstract, also in der Zusammenfassung des Papers, findet man an zahlenmäßigen Angaben zusätzlich zu den physikalischen Daten wie den Massen der Schwarzen Löcher, deren Abstand von der Erde und der abgestrahlten Energie noch eine weitere Angabe nämlich
to a significance greater than 5.1σ

aus B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) Phys. Rev. Lett. 116, 061102 – Published 11 February 2016 Creative Commons Attribution 3.0 License
Abbildung 2: Teils des Abstracts zum Paper
Weil ich dieses Konzept der Statistischen Signifikanz einerseits interessant und andererseits auch grundlegend für das Verständnis eines jeden Papers finde, will ich es hier in diesem Beitrag vorstellen. Dabei ist die Anwendung nicht nur auf die Physik beschränkt; die statistische Signifikanz kann man in allen Wissenschaftsfeldern antreffen, von der Physik über Chemie, Biologie bis hin zu Medizin und Psychologie.
Was außerdem noch dazukommt, ist, dass der Begriff nicht selbsterklärend ist und damit leicht zu Missverständnissen einlädt. Das hat gerade in letzter Zeit in der Fachwelt für Diskussionen gesorgt – so weit, dass dieses Jahr die American Statistical Association (ASA) zu diesem Thema ein Positionspapier [2] herausgegeben hat.
Das Wichtigste in Kürze
Von Statistischer Signifikanz wird in wissenschaftlichen Publikationen von Studienergebnissen gesprochen, wenn die Wahrscheinlichkeit, dass ein Testergebnis durch Zufall zustande gekommen ist, nicht über einer durch das Signifikanzniveau vorgegebenen Wahrscheinlichkeit liegt. Entgegen einer häufigen Vorstellung beschreibt das Signifikanzniveau damit nicht die Wahrscheinlichkeit, dass das Studienergebnis korrekt ist. Unkritisches und übertriebenes Vertrauen in die Statistische Signifikanz kann zu möglichen Fehlerquellen wie Publication Bias (Verzerrung aufgrund selektiver Veröffentlichung) und p-Hacking (nachträgliche Veränderung von Studien, um ein vorgegebenes Signifikanzniveau zu erreichen) führen, so dass inzwischen andere Ansätze zur Beurteilung der Qualität von Studien (Analyse mittels Bayes-Formel) an Bedeutung gewinnen.
So kurz so gut. Wenn wir uns näher mit dem Thema beschäftigen wollen, dann helfen die folgenden
Wichtigen Definitionen
p-value
Für ein beobachtetes, statistisches Messergebnis gibt der p-value die Wahrscheinlichkeit an, dass ein solches oder ein noch extremeres Ergebnis durch Zufall auftritt. Dazu wird das Gegenteil der Hypothese – eine Nullhypothese angenommen. Häufig ist das die Hypothese, dass gar kein Effekt vorhanden ist. Der p-value beschreibt dann, wie hoch die Wahrscheinlichkeit ist, dass trotz Vorliegen der Null-Hypothese das beobachtete Ergebnis durch Zufall auftritt.
Signifikanzniveau
Das Signifikanzniveau bezeichnet eine vorgewählte Wahrscheinlichkeit, ab der akzeptiert wird, dass ein Ergebnis wahrscheinlich nicht durch Zufall zustande gekommen ist. Das Signifikanzniveau ist im Prinzip frei wählbar. Häufig wird eine 95-prozentige Sicherheit gefordert, d.h. wenn kein Effekt vorliegt, dann soll nur in 5 % der Fälle ein Test fälschlicherweise ein positives Ergebnis liefern.
Statistische Signifikanz
Ein Ergebnis wird dann als statistisch signifikant bezeichnet, wenn sein p-value unter dem Signifikanzniveau liegt.
Sigma (σ)
In diesem Zusammenhang bezieht sich der griechische Buchstabe Sigma auf die Standardabweichung einer Normalverteilung. Diese ist so definiert, dass sich 68% der Werte einer zufälligen Verteilung in einem Bereich plus/minus einer Standardabweichung vom Mittelwert befinden und 32% außerhalb. Erweitert man den Bereich auf plus/minus 2 Sigma, dann liegen nur noch 5% der Ergebnisse außerhalb. Im zitierten Paper wird eine Signifikanz von 5,1 Sigma angegeben. Das bedeutet, dass die Wahrscheinlichkeit für einen Falschalarm (nämlich, dass das Ergebnis eine zufällige Schwankung des Hintergrundrauschens ist) kleiner als 2 × 10E-7 ist.
Und weil ich ja oben schon gesagt habe, dass ich gerne die Originalarbeiten zu einem Thema lese, habe ich natürlich auch zur Statistischen Signifikanz die erste Arbeit gesucht:
Geschichte
Der p-value wurde von Ronald Fisher [3] 1925 entwickelt, um einfach entscheiden zu können, ob ein Messergebnis ernst zu nehmen ist oder möglicherweise nur einen statistischen Ausreißer darstellt. Aufgrund der einfachen Verwendbarkeit durch Reduktion auf eine einzige Zahl hat der p-value große Verbreitung gefunden. Zunehmende Kritik an der unkritischen Verwendung des Konzepts der Statistischen Signifikanz (siehe z. B. Regina Nuzzo [4]) hat die American Statistical Association (ASA) dazu bewogen, 2016 ein Positionspapier [2] zu veröffentlichen, dass ausdrücklich vor einer missbräuchlichen Verwendung des p-values warnt.
Nachdem wir die trockenen Definitionen und die Geschichte hinter uns haben – ich tue mir immer leichter die abstrakten Erklärungen zu verstehen, wenn ich an einem konkreten Beispiel selber rechnen kann. Also kommen wir zur
Anwendung
Typischer Anwendungsbereich sind Studien z. B. in der Medizin, in denen zwei oder mehr Gruppen (Patienten oder Versuchstiere) sich in einer oder mehreren Variablen z. B. unterschiedliche Behandlung, aber auch Differenzen der Gruppen (Ernährung, Lebensweise, BMI, Raucher/Nichtraucher, …) voneinander unterscheiden. Da Krankheitsverläufe für verschiedene Personen und selbst für Versuchstiere einer Zucht/genetischen Linie unterschiedlich verlaufen, ist normalerweise das Ergebnis im Einzelfall nicht vorhersagbar. Um Aussagen machen zu können, werden die Ergebnisse der einzelnen Gruppen zusammengefasst – man kommt also um etwas Statistik nicht herum.
Anwendungsbeispiel
Es soll eine neue Behandlungsmethode für eine Erkrankung getestet werden, bei der sich ohne Behandlung 50% der Patienten von alleine erholen. Die neue Behandlungsmethode wird an 100 Personen getestet.
Aufgabenstellung
Ab wie vielen geheilten Patienten im Test kann davon ausgegangen werden, dass ein positives Behandlungsergebnis mit einer Sicherheit von mindestens 95% nicht durch Zufall entstanden ist, also signifikant ist?
Lösung
Nullhypothese ist hier also, dass die Behandlung keinen Effekt hat – dennoch kann ein Forscher auf den Fall stoßen, dass zufälligerweise mehr als die Hälfte der Patienten in der Studie geheilt werden. Jetzt müssen wir herausbekommen, wie wahrscheinlich das ist.
Für die genaue Lösung muss man auf die Formeln für die Binomial- bzw. näherungsweise auf die Gaußverteilung zurückgreifen. Zur Anschauung wird hier die Lösung aber graphisch hergeleitet.
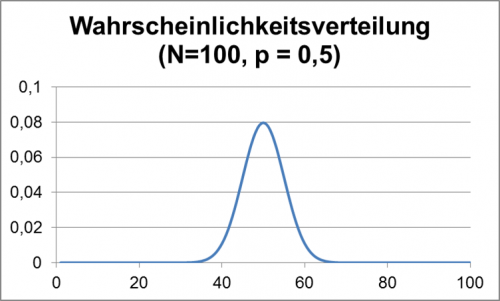
Im folgenden Diagramm wird gezeigt, mit welcher Wahrscheinlichkeit jedes Ergebnis, also eine bestimmte Zahl von geheilten Patienten, vorkommt, wenn man für jeden einzelnen der 100 Patienten jeweils unabhängig eine Heilungswahrscheinlichkeit von 50% ansetzt. (Man kann sich vorstellen, dass man für jeden Patient eine Münze – Heilung oder nicht – wirft. Das Problem ist mathematisch äquivalent.)
Abbildung 3: Wahrscheinlichkeitsverteilung für 100 Münzwürfe
Wie man sieht, ist z. B. die Wahrscheinlichkeit in einem Versuch genau 50 geheilte Patienten zu finden 0,08 = 8%. Die Wahrscheinlichkeiten nehmen links und rechts dazu schnell ab, d. h. größere Abweichungen vom mittleren Wert sind selten.
Für die Aufgabe ist nun zu bestimmen, wo man eine Linie in dem obigen Diagramm setzen müsste, dass 95% der Ergebnisse sich links davon befinden, so dass die Wahrscheinlichkeit für ein Ergebnis rechts der Linie nur noch 5% beträgt.
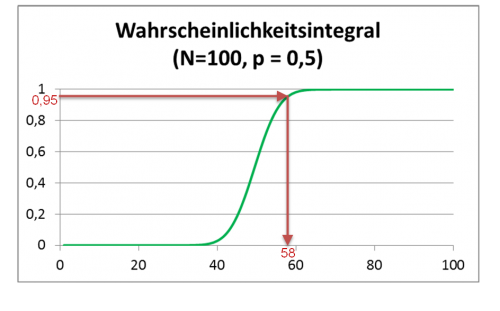
Die Summe aller Wahrscheinlichkeiten für ein Ergebnis kleiner einer Zahl ist in der folgenden Graphik gezeigt:
Abbildung 4: Wahrscheinlichkeitsintegral für 100 Münzwürfe
Durch die roten Linien im Diagramm ist gezeigt, wie man die zu einer integrierten Wahrscheinlichkeit von 95% gehörige Anzahl von geheilten Personen ablesen kann. In unserem Beispiel ergibt sich, dass erst wenn mindestens 58 Personen im Test geheilt wurden, man sich zu 95% sicher sein kann, dass nicht nur durch einen glücklichen Zufall überdurchschnittlich viele Testpersonen geheilt wurden.
Trotz allem – auch die Statistische Signifikanz ist nur ein Werkzeug und wie jedes andere Werkzeug kann auch dieses falsch eingesetzt werden. Daher ist es also gut, die diversen Fallstricke zu kennen, um nicht selber darauf hereinzufallen (gerade bei der eigenen Lieblingstheorie muss man besonders vorsichtig sein – unser Hirn macht uns da gerne etwas vor) oder sich etwas unterschieben zu lassen (Marketing, sensationshungrige Presse, politische Interessen, Profitgier, skrupellose Kollegen – hier können Sie Ihr eigenes Feindbild einsetzen – könnten versucht haben, dass Ergebnis in deren Richtung zu verschieben).
Diskussion
Es muss darauf hingewiesen werden, dass es für die Interpretation der Signifikanz in obigem Beispiel wesentlich ist, dass die Fragestellung im Voraus und eindeutig formuliert wurde und keine weiteren Fragestellungen in Betracht gezogen wurden. Mögliche Fehlerquellen könnten sein: Der Forscher erhebt verschiedene Datensätze (z. B. könnte der Heilerfolg an verschiedenen Tagen und an Hand verschiedener Parameter (Patientenbefragung, Laborwerten, Verbrauch an Schmerzmitteln) erfasst werden). Damit erhöht sich die Chance, bei einem der Parameter einen signifikanten Effekt zu sehen.

xkcd-Comics, Randall Munroe, https://xkcd.com/882/, Creative Commons Attribution-NonCommercial 2.5 License
Abbildung 5: xkcd-Comic significance
Was auch geht, der Forscher ändert die Fragestellung (z. B. könnte der Forscher beschließen, auch eine deutlich geringere Zahl von geheilten Patienten wäre ein Nachweis, dass eine Behandlung anschlägt (Erstverschlimmerung) und somit würde er nachträglich auch Ergebnisse z. B. unter 42 geheilten Patienten als signifikant berichten.
Des Weiteren sagt das Signifikanzniveau nicht direkt etwas über die Wahrscheinlichkeit aus, dass bei einem positiven Testergebnis die Hypothese richtig ist. Gerade beim Test von a priori unwahrscheinlichen Hypothesen ergibt sich zwingend, dass die meisten positiven Testergebnisse falsch sind und zufällig entstanden sind [5] (für ein Rechenbeispiel hierzu siehe Kann ich meinem Hirn trauen? (3. Teil)).
Kritik
Fehlerhafte Interpretationen von Statistischer Signifikanz
Statistische Signifikanz macht keine Aussage darüber, ob die Hypothese richtig ist. Es wird nur angegeben, wie wahrscheinlich bei zutreffender Null-Hypothese das vorliegende Ergebnis ist. Alternative Hypothesen, die das vorliegende Ergebnis ebenso gut oder besser erklären können, werden nicht berücksichtigt. Statistische Signifikanz macht keine Aussage über die Größe oder Relevanz eines Effekts. Mit entsprechend aufwändigen Tests (z. B. mehr Versuchspersonen) können auch kleine Effekte signifikant nachgewiesen werden, auch wenn diese Effekte in der Praxis vernachlässigt werden können.
Willkürliche Definition der Schwelle für statistische Signifikanz
Der häufig verwendete Wert für das Signifikanzniveau von 0,05 ist willkürlich gewählt und gerade bei Tests von grundlegender Bedeutung zu niedrig angesetzt. In der Physik wird deshalb als Schwelle für den Nachweis von bisher nicht bestätigten Phänomenen ein Signifikanzniveau von p < 3 × 10E-7 (entsprechend 5σ) verwendet (wie oben im Paper zum Nachweis der Gravitationswellen, aber auch beim Nachweis des Higgs-Bosons [6]), obwohl es sich dabei um theoretisch erwartete Phänomene mit vorhandenen indirekten Hinweisen ihrer Existenz handelte. Für gänzlich unerwartete Effekte müsste die Schwelle daher sogar noch höher angesetzt werden. Hier muss ich noch einen Seitenhieb auf diverse Pseudowissenschaftler loswerden – wenn man schon versucht, neue Physik wie ein Gedächtnis des Wassers etc. zu etablieren, dann ist schon mehr als Nachweis nötig als eine „signifikante“ Studie mit Signifikanzniveau 5%).
Bayes-Analyse als Alternative zum p-value
Als Alternative zum p-value schlagen Goodman [7] und Steven Novella [8] vor, bei der Analyse von Studienergebnissen den Satz von Bayes zu verwenden. Im Gegensatz zum p-value kann durch den Satz von Bayes vorhergehendes Wissen zur Wahrscheinlichkeit einer Hypothese mit herangezogen werden. Die bayessche Statistik kann dann angeben, wie sich eine a priori vorhandene Wahrscheinlichkeit durch neue Studienergebnisse verändert. Ein Punkt der hingegen an der Bayes-Analyse kritisiert wird, ist, dass ohne vorheriges Wissen die Festlegung der a priori Wahrscheinlichkeit ebenfalls willkürlich ist. Z. B. können verschiedene Personen ganz unterschiedlicher Meinung sein, wie wahrscheinlich vor einer Studie die Wahrscheinlichkeit ist, dass etwa Homöopathika irgendeine Wirkung haben. Allerdings zwingt die Bayes-Analyse einen dazu, sich dazu Gedanken zu machen, diese zu quantifizieren und die eigene Wahl zu begründen.
Statistische Signifikanz als Schranke für die Veröffentlichung
Häufig wird ein Erreichen eines Signifikanzniveaus von p < 0,05 als Voraussetzung für eine Veröffentlichung in einer Fachzeitschrift gefordert. Dies führt zu einer Verzerrung (publication bias) der Ergebnisse, so dass statistische Ausreiser übermäßige Bedeutung bekommen, während Ergebnisse, die keinen Effekt zeigen, verloren gehen. Durch das Fehlen der erfolglosen Studien wird eine Wirksamkeit vorgetäuscht, die in Wirklichkeit nicht vorhanden ist. Daher ist zum Beispiel die Fachzeitschrift Basic and Applied Social Psychology dazu übergegangen, in ihren Veröffentlichungen den p-value nicht mehr zu verwenden [9].
Veränderung von Studien um Signifikanz zu erreichen (“p-hacking” or “researcher degrees of freedom”)
Simonsohn, Nelson und Simmons konnten nachweisen [10], dass sich die p-values in Veröffentlichungen auffällig häufig knapp unter 0,05 häufen. Als möglichen Grund führen sie an, dass Freiheiten des Forschers bei der Datensammlung, Analyse und Darstellung es erlauben, die vorliegenden Daten auch bei feststehender Fragestellung auf vielerlei Weise auszuwerten [11]. Ein Forscher könnte z. B. eine Befragung dann verlängern, wenn sich noch kein signifikanter Effekt zeigt und dann beenden, wenn die Signifikanz erreicht wurde. In [12] zeigen Andrew Gelmany und Eric Lokenz beispielhaft an realen Papern wie so etwas vor sich gehen kann.
Dass in der akademischen Welt ein gewisser Druck herrscht, zu veröffentlichen und dafür signifikante Ergebnisse produziert werden müssen, verschärft das Problem noch.
Ein Ansatz, den Einfluss sowohl von nicht veröffentlichten als auch von im Verlauf abgeänderten Studien zu begrenzen, ist die Initiative AllTrials[12], die u. a. fordert, Studien noch vor ihrem Beginn und einschließlich einer Beschreibung des geplanten Vorgehens zu registrieren.
Und weil es dort schon so schön zusammengefasst wurde, will ich aus dem oben erwähnten Positionspapier der American Statistical Association zitieren für das
Schlusswort
„Gutes statistisches Vorgehen, als ein wesentlicher Bestandteil guten wissenschaftlichen Vorgehens, betont die Prinzipien guten Studiendesigns und guter Durchführung einer Studie, eine Vielfalt von zahlenmäßigen und graphischen Zusammenstellungen der Daten, ein Verständnis des untersuchten Phänomens, die Interpretation der Ergebnisse im Kontext, das vollständige Offenlegen und geeignetes logisches und quantitatives Verständnis davon, was die Datenzusammenstellungen bedeuten.
Kein einzelner Zahlenwert sollte das wissenschaftliche Denken ersetzen.“
Quellen- und Literaturangaben
[1] B.P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) Phys. Rev. Lett. 116, 061102 – Published 11 February 2016 https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.116.061102
[2] Ronald L. Wasserstein & Nicole A. Lazar 2016): The ASA’s statement on p-values: context, process, and purpose, The American Statistician, https://dx.doi.org/10.1080/00031305.2016.1154108
[3] Fisher, Ronald A. (1925). Statistical Methods for Research Workers. Edinburgh, UK: Oliver and Boyd. p. 43. ISBN 0-050-02170-2
[4] Spektrum der Wissenschaft, 2014, Regina Nuzzo:„Wenn Forscher durch den Signifikanztest fallen“ https://www.spektrum.de/news/statistik-wenn-forscher-durch-den-signifikanztest-fallen/1224727 (aufgerufen am 27.März 2016), Original: “Statistical errors”, Nature 506, S. 150-152, 2014 https://www.nature.com/news/scientific-method-statistical-errors-1.14700 (aufgerufen am 30.März 2016)
[5] Why Most Published Research Findings Are False; John P. A. Ioannidis; PLOS; Published: August 30, 2005; https://dx.doi.org/10.1371/journal.pmed.0020124
[6] CERN experiments observe particle consistent with long-sought Higgs boson. Pressemitteilung von CERN. 4.Juli 2012. https://press.cern/press-releases/2012/07/cern-experiments-observe-particle-consistent-long-sought-higgs-boson aufgerufen am 7.4.2016
[7] Toward Evidence-Based Medical Statistics. 2: The Bayes Factor; Steven N. Goodman, MD, PhD; Ann Intern Med. 1999 Jun 15;130(12):1005-13
[8] P Value Under Fire; Steven Novella; 9.3.2016 https://www.sciencebasedmedicine.org/p-value-under-fire/#more-41146 aufgerufen am 7.4.2016
[9] Psychology journal bans P values; Chris Woolston; 09 March 2015;
https://www.nature.com/news/psychology-journal-bans-p-values-1.17001 aufgerufen am 11.4.2016
[10] P-curve: A key to the file-drawer; Simonsohn, Uri; Nelson, Leif D.; Simmons, Joseph P.; Journal of Experimental Psychology: General, Vol 143(2), Apr 2014, 534-547. https://dx.doi.org/10.1037/a0033242
[11] False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant; Joseph P. Simmons, Leif D. Nelson und Uri Simonsohn; https://www.ncbi.nlm.nih.gov/pubmed/22006061
[12] The garden of forking paths: Why multiple comparisons can be a problem, even when there is no \
shing expedition” or \p-hacking” and the research hypothesis was posited ahead of time;Andrew Gelmany and Eric Lokenz
https://www.stat.columbia.edu/~gelman/research/unpublished/p_hacking.pdf
[13] https://www.alltrials.net/find-out-more/all-trials
Originalzitate
“Good statistical practice, as an essential component of good scientific practice, emphasizes principles of good study design and conduct, a variety of numerical and graphical summaries of data, understanding of the phenomenon under study, interpretation of results in context, complete reporting and proper logical and quantitative understanding of what data summaries mean. No single index should substitute for scientific reasoning.”
aus Ronald L. Wasserstein & Nicole A. Lazar 2016): The ASA’s statement on p-values: context, process, and purpose, The American Statistician, https://dx.doi.org/10.1080/00031305.2016.1154108
Bildnachweis
Abbildung 1 und 2: aus B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration) Phys. Rev. Lett. 116, 061102 – Published 11 February 2016 Creative Commons Attribution 3.0 License
Abbildung 3 und 4: Autor
Abbildung 5: xkcd-Comics, Randall Munroe, https://xkcd.com/882/, Creative Commons Attribution-NonCommercial 2.5 License











Kommentare (49)