Der Physik-Nobelpreis 2016 wurde verliehen. Nicht für die Gravitationswellen oder die anderen vorhergesagten Themen. Sondern eher überraschend für etwas Kompliziertes mit Quanten! Oder, wie es der Journalist Ben Hammersley ausgedrückt hat:
Oh balls, it's something quantum and weird, sigh science journalists worldwide, closing their half-written LIGO drafts.
— Ben Hammersley (@benhammersley) 4. Oktober 2016
Ja, “quantum und weird” trifft es recht gut. Ich habe den Nachmittag damit verbracht zu verstehen, um was es da geht. Ich habe vor allem versucht zu verstehen, um was es überhaupt geht und was jetzt bei all dem Gerede und Getwitter über “topologische Isolatoren”, “Quanten-Hall-Effekt”, “Donuts”, und “Symmetriebrechung” jetzt eigentlich das Ding war, was das Nobelkomitee mit dem Preis ausgezeichnet hat. Selbst die meisten Experten die ich kontaktiert hatte, konnten so spontan nicht aushelfen.
Aber egal – ich habe einfach mal probiert, mein bestes zu geben und möchte euch hier die Resultate meiner Recherche präsentieren. Nachdem ich einen Nachmittag lang die Materialien des Nobelkomitees studiert und diverse verfügbare Medienberichte gelesen, stellt sich der Nobelpreis für Physik des Jahres 2016 aus meiner Laienhaften Sicht so dar wir unten beschrieben. Wenn jemand mitliest und besser über das Thema Bescheid weiß als ich, dann bitte ich sehr darum, in den Kommentaren zur Aufklärung der Angelegenheit beizutragen (Und ich möchte noch anmerken, dass es seine sehr instruktive Übung war, ein komplexes wissenschaftliches Thema von dem ich so gut wie keine Ahnung habe nur anhand der vorhandenen medialen Aufarbeitung verstehen zu wollen. Das zeigt umso mehr, wie wichtig vernünftiger Wissenschaftsjournalismus und vernünftige Wissenschaftskommunikation ist).
——————————
Der Nobelpreis für Physik des Jahres 2016 geht an die britischen Forscher David Thouless, Duncan Haldane und Michael Kosterlitz. Und zwar für “theoretische Entdeckungen von topologischen Phasenübergängen und topologische Zustände von Materie”. Das klingt beeindruckend, aber auch ein wenig vage.
Was ein Phasenübergang ist, ist noch leicht zu erklären. Man kennt ja die drei Aggregatzustände der Materie: Fest, flüssig und gasförmig und wenn die Materie von einem Zustand in den anderen wechselt, dann ist das ein Phasenübergang. Flüssiges Wasser das gefriert durchläuft einen Phasenübergang. Genauso wie flüssiges Wasser, das verdampft. Aber neben diesen drei klassischen Aggregatzuständen gibt es auch noch einige andere Zustände, die im Alltag eher nicht auftreten. Nur bei enorm hohen Temperaturen kann ein Gas zum Beispiel in einen Plasmazustand übergehen; dann lösen sich die Elektronen aus der Hülle der Atomkerne und bewegen sich frei herum. Bei sehr kalten Temperaturen gibt es wieder andere Zustände – da kann Materie zum Beispiel nicht einfach nur flüssig sein, sondern “supraflüssig”, also fließen ohne dabei einen Widerstand zu spüren. Auch die Supraleitfähigkeit ist so ein extremer Zustand.
Aber nicht nur die Temperatur beeinflusst die Zustände und Phasenübergänge. Auch die räumlichen Eigenschaften spielen eine Rolle. Normalerweise nehmen die Atome der Materie immer einen dreidimensionalen Raum ein. Unter bestimmten Umständen kann man sie aber auch “zweidimensional” anordnen, also Flächen erzeugen, die nur aus einer einzigen Atomschicht bestehen (wie zum Beispiel das Material Graphen, für dessen Untersuchung der Physik-Nobelpreis des Jahres 2008 verliehen wurde).
David Thouless, Duncan Haldane und Michael Kosterlitz haben in den 1970er und 1980er Jahren untersucht, wie sich Phasenübergänge in so einer zweidimensionalen Welt abspielen. Ein Phänomen, bei der so eine Analyse eine Rolle spielt (und dessen Analyse durch die Arbeit der Nobelpreisträger überhaupt erst möglich geworden ist) sind sogenannte “topologische Isolatoren”. Dabei handelt es sich um einen Festkörper, der sich in seinem Inneren wie ein elektrischer Isolator verhält, also keinen elektrischen Strom leitet. Seine Oberfläche, also die Außenseite ist dagegen sehr stark leitfähig, fast so wie ein Supraleiter. Das alleine wäre aber noch nicht das bemerkenswerte. Das besondere an den topologischen Isolatoren ist die Art und Weise, wie sich die Elektronen an seiner Oberfläche bewegen.

Ein Isolator (nicht topologisch) (Bild: Wikipedia, CC-BY-SA 3.0)
Ein Isolator kann deswegen keinen Strom leiten, weil die Elektronen in den Hüllen seiner Atome stark an den Atomkern gebunden sind und nicht frei fließen können. Bei guten elektrischen Leitern befinden sich jedoch viele Elektronen weit enfernt vom Atomkern und können sich quasi losreißen und bewegen: Das Material ist leitfähig. Bei den topologischen Isolatoren muss man aber auch noch den Spin berücksichtigen und wenn in der Quantenmechanik der Spin ins Spiel kommt, wird es immer kompliziert. Man stellt sich Teilchen wie Elektronen ja gerne als kleine Kugeln vor und ihren Spin als die Richtung, in der sie um ihre Achse rotieren. Aber Elektronen sind eben keine kleinen Kugeln und da rotiert auch nichts im klassischen Sinn. Eigentlich ist der Spin nur eine physikalische Eigenschaft, die ein Elektron haben kann und für die es keine Entsprechung in der Alltagswelt gibt.
Aber die Elektronen haben nun einen Spin und dank dieses Spins können sie wie kleine Magnete wirken. Jetzt wird es komplex: Elektrisch geladene Teilchen die sich bewegen, wie die Elektronen, erzeugen ein Magnetfeld. Und weil sie dank des Spins selbst wie Magnete wirken, spüren sie magnetische Kraft. Die Bewegung der Elektronen wird also einerseits vom Magnetfeld beeinflusst; erzeugt das Magnetfeld aber andererseits selbst wieder erst.
Je nach Material kann diese Kopplung zwischen Bewegung und Magnetfeld stärker oder schwächer sein. Und bei topologischen Isolatoren ist sie so stark, dass die ganze Struktur der Elektronenverteilung durcheinander gebracht wird. Elektronen, die sonst stark an den Atomkern gebunden wären, können sich nun doch frei bewegen. Aber auch nur innerhalb gewisser Grenzen. Der Spin der Elektronen, der zwei verschiedene Werte annehmen kann, bestimmt, ob sie sich – vereinfacht gesagt – von links nach rechts oder von rechts nach links bewegen können.
Wie das genau abläuft und bei welchen Materialen das funktioniert, wird von der Topologie bestimmt. Genau das war die Entdeckung, die die drei Nobelpreisträger gemacht haben und genau das ist auch der Punkt, an dem man Donuts und Brezeln erwähnen muss. Der Vergleich ist zwar nicht mehr sonderlich originell, weil er seit Jahrzehnten von Mathematikern und Physikern zur Erklärung der Topologie benutzt wird, aber ich will mich dieser Tradition natürlich nicht entgegenstellen. Außerdem hatte ich Hunger und mir daher einen Krapfen (aka “Berliner” aka “Pfannkuchen), einen Donut und eine Brezel gekauft.
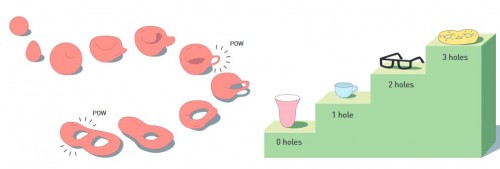
Diese drei Objekte unterscheidet natürlich jede Menge. Sie sind unterschiedlich groß, unterschiedlich schwer und schmecken auch ganz unterschiedlich. Aber in der Topologie spielt das alles keine Rolle. Hier geht es einzig und allein um die Form. Man kann sich im Rahmen der Topologie jedes Objekt so vorstellen, als würde es aus einer beliebig verformbaren Gummimasse bestehen. Und sieht dann alle Objekte als identisch an, die sich ohne Gewaltanwendung (das heißt zerreissen oder Löcher bohren) ineinander umwandeln lassen. Aus meinem Krapfen (dessen Verformbarkeit ich jetzt einfach mal voraussetze) könnte ich zum Beispiel problemlos eine Schüssel machen. Ich müsste nur in die Mitte eine Vertiefung drücken und dann die Seiten ein wenig nach oben ziehen. Ein Krapfen und eine Schüssel sind topologisch also identisch. Aber egal was ich anstelle: Ich werde aus dem Krapfen niemals einen Donut machen können, ohne irgendwo ein Loch bohren und das Material zerreissen zu müssen. Ein Krapfen und ein Donut sind topologisch also unterschiedlich. Ein Donut und eine Kaffeetasse mit Henkel dagegen wieder nicht. Das erscheint seltsam, ist aber so: Eine Gummitasse mit Henkel kann man leicht zu einem Donut umformen; man muss nur das Material das die Tasse ausmacht so lange herum ziehen und zerren und um die Öffnung verschmieren, die der Henkel umschließt bis alles gleichmäßig verteilt ist und schon hat man einen Donut. Bei der Brezel ist es wieder anders; die hat in diesem Fall drei Löcher und kann nicht zu einem Donut (oder einer Kaffeetasse) mit nur einem Loch verformt werden.
Kurz gesagt: Die Objekte in der Topologie unterscheiden sich vor allem in der Anzahl der Löcher (und Knoten) die sie haben. Das alles hat jetzt vorerst noch nichts mit dem Nobelpreis zu tun – die mathematische Disziplin der Topologie gibt es schon viel länger – aber es ist der Teil der ganzen Geschichte der sich am besten erklären lässt…
Die drei Nobelpreisträger jedenfalls haben die Methoden der Topologie benutzt um die Eigenschaften von Phasenübergängen an den Oberflächen von Festkörpern zu untersuchen. Und dabei jede Menge interessante Entdeckungen gemacht. Zum Beispiel, dass es hier ganz besondere Arten von Phasenübergangen gibt, die keine Symmetrien brechen. Symmetriebrechung bei Phasenübergängen klingen zwar wild, sind aber normal. Flüssiges Wasser in dem die Wassermoleküle zufällig und ständig herumwirbeln, sieht in jeder Richtung gleich aus. Friert es aber und wird fest, ordnen sich die Moleküle in Kristallgittern an und es gibt nun Richtungen die anders aussehen als andere. Die Symmtrie des flüssigen Wassers ist beim festen also gebrochen.
Bei den topologischen Phasenübergangen an den Oberflächen von Festkörpern ist das allerdings nicht immer der Fall. Hier gibt es Symmtrien, die auch weiterhin bestehen, egal welchen Zustand der Festkörper einnimmt. Mit den theoretischen Methoden die von David Thouless, Duncan Haldane und Michael Kosterlitz entwickelt wurden, konnte man das nun nicht nur verstehen, sondern auch ausführlich untersuchen. Und so auch Phänomene wie die Supraleitfähigkeit besser verstehen als früher.
Nicht nur das: Das bessere Verständnis der seltsamen Eigenschaften dieser Materie erlaubt auch neue Anwendungen. Die topologischen Isolatoren konnten 2005 schon im Labor hergestellt werden und man macht sich Hoffnungen, sie irgendwann mal als Bauteile neuer und viel besserer Computer verwenden zu können. Die theoretischen Physiker dagegen sind eher daran interessiert, ganz neuen Materialien zu konstruieren, die sich an ihren Grenzflächen noch seltsamer verhalten. Mit der Arbeit der Nobelpreisträger kann man auch “topologische Supraleiter” beschreiben in denen Quantenzustände herrschen, die simulieren wie sich zum Beispiel die lang gesuchte aber noch immer nicht entdeckte dunkle Materie verhalten könnte.
In drei Worten zusammengefasst lautet die Arbeit der Physik-Nobelpreisträger des Jahres 2016: “Irgendwas Kompliziertes mit Quanten” (ok, das waren vier – selbst für eine blöde Witzantwort in drei Worten ist das Thema zu komplex). Etwas länger und seriöser zusammengefasst: Die drei Wissenschaftler haben spezielle mathemtische Methoden zur Untersuchung der Eigenschaften von Materie entwickelt. Dabei haben sie festgestellt, dass diese Eigenschaften oft von der Form der Oberfläche dieser Materialien abhängt und durch das Wechselspiel von Topologie und Quantenmechanik die seltsamen Quanteneffekte die man sonst nur aus der Mikrowelt einzelner Atome kennt auch im großen Maßstab der normalen Welt auftreten können.
Auf jeden Fall: Gratulation an die Preisträger!
(Der Quanten-Hall-Effekt! Verdammt! Ich hab den Quanten-Hall-Effekt vergessen!)













Kommentare (45)