Hinweis: Dieser Artikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb 2016. Hinweise zum Ablauf des Bewerbs und wie ihr dabei Abstimmen könnt findet ihr hier.

Das sagt der Autor des Artikels,
Keine Angabe
——————————————
Die Informationstheorie ist eines der eher trocken erscheinenden Themen der Informatik. Tatsächlich steckt sie voller Begriffe wie Entropie oder Informationsgehalt. Mich selbst hatte bei der ersten Bekanntschaft besonders die Tatsache irritiert, dass der Informationsgehalt in Bits gemessen wird, also der selben Einheit, die auch die kleinste Speichereinheit in Computern bezeichnet Ein solches – ich nenne es mal binäres Bit, auch wenn das doppelt gemoppelt ist, da Bit für binary digit steht, aber es löst hoffentlich die Doppeldeutigkeit auf – kann entweder den Zustand 0 oder 1 haben. Doch der Informationsgehalt eines einzelnen binären Bits kann von 0 bis theoretisch Unendlich reichen. Warum das möglich ist, will ich mit diesem Artikel versuchen zu erläutern.
Ich beginne direkt einmal mit der Formel, die tatsächlich gar nicht mal so lang ist:
Dabei ist x das zu betrachtende Zeichen, I der Informationsgehalt, px die Auftrittswahrscheinlichkeit von x und a die Basis des verwendeten Zahlensystems (beim Binärsystem also 2, beim Dezimalsystem 10 und bei deutschen Wörtern 30, wenn man Groß-/Kleinschreibung ignoriert aber ä,ö,ü und ß mit einbezieht). Das Ergebnis ist die Anzahl der Zeichen (die jeweils a verschiedene Werte haben können), die (mit dem Vorwissen über die Wahrscheinlichkeiten) mindestens benötigt werden, um die Informationen zu speichern oder zu übertragen. Überlicherweise wird für a einfach 2 verwendet, damit ist das Ergebnis die Anzahl der Binärziffern der diese Information entspricht, die Einheit ist also Bit. Verwendet man eine andere Basis erhält man auch eine andere Einheit, entsprechend dem Zahlensystem.
Der Informationsgehalt eines Zeichens ist also davon abhängig, wie hoch die Auftrittswahrscheinlichkeit für dieses Zeichen ist, das heißt, wie hoch die Wahrscheinlichkeit ist genau dieses Zeichen an dieser Stelle zu erhalten. Je niedriger die Wahrscheinlichkeit ist, desto höher ist der Informationsgehalt. Ein einfaches Beispiel, in folgendem Wort fehlt lediglich der letzte Buchstabe: “Wahrscheinlichkei_”. Nun, jeder der das Wort kennt (das werden vermutlich Alle sein) wird fast automatisch das fehlende “t” einsetzen. Die Auftrittswahrscheinlichkeit des “t” war also sehr hoch, sein Informationsgehalt daher sehr gering. Ein weiteres Beispiel, wieder fehlt lediglich der letzte Buchstabe: “Kei_”. Was könnte da nun folgen? Geht man die Buchstaben durch, merkt man, dass mehrere Wörter möglich sind, beispielsweise “Keil”, “Keim” oder “Kein”. Hier ist der Informationsgehalt des letzten Zeichens also höher, da mehrere Buchstaben gleich wahrscheinlich sind. Da das Wort alleine steht hilft auch der Großbuchstabe nicht bei der Identifikation, was direkt zum nächstens Beispiel führt, diesmal ein Satz: “Sie hielt die Tür mit einem Kei_ offen.” Angenommen, der Verfasser hat keinen Fehler gemacht, fällt das Wort “kein” allein schon wegen des Großbuchstabens raus (es macht aber hier auch keinen Sinn). Ein Keim wäre vermutlich wenig geeignet, eine Tür offen zu halten, übrig bleibt also nur der Keil. Obwohl sich am Wort nichts geändert hat, ist nur durch den Kontext der Informationsgehalt des “l” gesunken.
Betrachten wir nochmal das einzelne Wort “Kei_”: Welcher Buchstabe hätte an der letzten Stelle den höchsten Informationsgehalt? Den höchsten Informationsgehalt hat das Zeichen mit der niedrigsten Auftrittswahrscheinlichkeit, welches ist hier also am unwahrscheinlichsten? Das lässt sich nicht mit Sicherheit beantworten, ein sehr guter Kandidat wäre jedoch das “q”. Es ist (laut Wikipedia, dem kann man in diesem Fall denke ich auch ohne weitere Quelle vertrauen) der seltenste Buchstabe in deutschen Texten und es gibt auch kein deutsches Wort “Keiq”. Es erscheint möglicherweise paradox, aber obwohl dadurch nur ein Unsinnswort entstanden ist, trägt das “q” viel Information. Das ergibt sich jedoch direkt aus der Definition des Informationsgehalts: Das q ist an dieser Stelle unerwartet, es passt in kein bekanntes Muster und ist daher etwas Neues, sprich eine neue Information. Der Informationsgehalt sagt also offenbar nichts darüber aus, wie nützlich oder wichtig die Information für den Empfänger ist, sondern nur, wie erwartbar sie ist.
An den Beispielen erkennt man vielleicht schon: Der Informationsgehalt ist vom Wissen des Empfängers abhängig. Um ein fehlendes Zeichen passend ergänzen zu können, muss man das Wort schon kennen. Ein Extrembeispiel, diesmal mit einem Binärwort: Stellt euch vor, ihr seid ein Computer und erhaltet eine Nachricht. Ihr wisst bereits mit 100% Sicherheit, dass die Nachricht “01000001” (das ist der ASCII-Code für “A”) lauten wird. Welchen Informationsgehalt wird die Nachricht für euch haben? Die Antwort ist recht trivial: Da ihr bereits sicher wisst, was ihr erhaltet, ist der Informationsgehalt genau 0 Bit. Das ist natürlich idealisiert, denn in Realität könnten immer noch Übertragungsfehler auftreten oder ihr erhaltet doch eine andere Nachricht als erwartet. Dann wären es etwas über 0 Bit, aber nicht viel. Ihr habt also 8 (binäre) Bits übertragen bekommen, die für euch jedoch 0 Bit Information tragen. Die Übermittlung war dementsprechend überflüssig. Diese 0 Bit lassen sich auch mit der Formel bestätigen. Die Auftrittswahrscheinlichkeit ist hier für jedes Zeichen gleich, nämlich 1. Damit ergibt sich:
Der Logarithmus von 1 ist immer 0, egal zu welcher Basis.
Wie könnte man den umgekehrten Fall erreichen, also ein Zeichen mit einem unendlichen Informationsgehalt? Dafür bräuchte man ein Zeichen, dessen Auftrittswahrscheinlichkeit gegen 0 geht, die Wahrscheinlichkeit also unendlich klein (aber nicht 0!) ist. Das ist natürlich wieder in Realität nicht machbar. Genauso wie bei einem Zeichen, das eine Wahrscheinlichkeit von genau 0 hat. Erhalten wir es dennoch, dann hat es keinen unendlichen Informationsgehalt, sondern wir haben einen Widerspruch im System, das Zeichen hätte schließlich niemals auftreten dürfen.
Bisher ging es nur um den Informationsgehalt eines einzelnen Zeichens oder um eine Nachricht, die uns überhaupt keine Information liefert. Das ist im Normalfall natürlich anders, also braucht man den gesamten Informationsgehalt einer Nachricht. Dieser lässt sich jedoch einfach bestimmen, indem man die Informationsgehalte der einzelnen Zeichen addiert. Mal ein vereinfachtes Rechenbeispiel: Das Wort “Fernbedienung” (es lag halt grade eine vor mir auf dem Tisch) enthält 13 Zeichen, aber nur 9 davon sind unterschiedlich. Das e und das n kommen jeweils drei mal vor. Die Auftrittswahrscheinlichkeiten für e und n sind also 3/13. Für f, r, b, d, i, u und g sind sie nur 1/13. (Das ist jedoch wie gesagt eine vereinfachte Rechnung, da keinerlei Vorwissen einbezogen wird, aber die Rechnung wird so deutlich leichter.) Der gesamte Informationsgehalt ist also:
Für das Wort “Fernbedienung” braucht man also mindestens 4,8 Byte (3 Bit pro Zeichen), deutlich weniger als die 13 Byte, die das Wort in typischer UTF-8-Kodierung braucht. Theoretisch sollte ein Kompressionsalgorithmus (wie beispielsweise der Deflate-Algorithmus, der für ZIP-Archive verwendet wird) also in der Lage sein, den Platzbedarf des Wortes auf 4,8 Byte zu reduzieren, praktisch ist das bei solch einem kurzen Text allerdings nicht der Fall, da Kompressionsverfahren auch immer einen Overhead erzeugen, also selbst Platz verbrauchen um die für die Dekompression benötigten Informationen zu speichern. Im schlimmsten Fall kann eine komprimierte Datei sogar geringfügig größer sein als vorher, das kommt jedoch eher selten vor.
Ein reales Beispiel für Datenkompression: Dieser Text ist 7810 Bytes lang (zumindest war das so, als ich dies hier schrieb). Dass die Zeilenumbrüche im Windows-Stil (bei Linux und Mac ist das anders) immer 2 Byte verbrauchen ignoriere ich hier der Einfachheit halber, das macht die Zahlen nur unschön und ändert sehr wenig. Unkomprimiert braucht jedes Zeichen 8 Bit (UTF-8-Kodierung). Komprimiert als ZIP-Archiv belegt die Datei nur noch 3363 Byte Speicherplatz, das ergibt etwa 3,44 Bit pro Zeichen. Mein Text hat also in etwa einen Informationsgehalt von 3,44 Bit pro Symbol, ich hätte mir also mehr als jedes zweite Zeichen sparen können (Nein, so funktioniert das natürlich nicht. 😉 ). Der bzip2-Algorithmus schafft es sogar mit noch etwas weniger: 3079 Bytes (ca. 3,15 Bit pro Zeichen). Das liegt ja schon sehr nah an dem für “Fernbedienung” berechneten Wert und zeigt, dass die Algorithmen schon sehr gut arbeiten.
Jetzt stellt man sich vielleicht die Frage: Welcher Text würde denn einen Informationsgehalt haben der auch seinem Platzbedarf entspricht, sprich, was lässt sich überhaupt nicht komprimieren? Die Antwort: Zufallszahlen. Probiert es aus: Werft 1000 Münzen, schreibt die Ergebnisse als einzelne Bits in eine Datei (Ja, ich weiß, das geht mit normalen Texteditoren nicht aber wer einen HEX-Editor hat kann es probieren) und versucht das zu komprimieren. Wenn ihr keine Lust habt 1000 Münzen zu werfen (das geht doch ganz schnell), verwendet einen echten Zufallszahlengenerator wie beispielsweise random.org (was echte Zufallszahlengeneratoren von Pseudozufallszahlengeneratoren unterscheidet ist noch ein anderes Thema).
Was ich über die Kompressionsverfahren geschrieben habe gilt natürlich nur für verlustfreie Verfahren, wie beispielsweise ZIP. Verlustbehaftete Verfahren (zum Beispiel MP3 oder JPEG) dagegen tricksen mit der menschlichen Wahrnemung und reduzieren tatsächlich die Information, entfernen also nicht nur Unnötiges. Wird das jedoch geschickt gemacht fällt es uns nicht weiter auf, aber technisch gesehen sind Informationen verlorengegangen.
Ich hoffe, dass das Konzept der Information damit ein wenig klarer geworden ist. Es ist ein sehr komplexes Thema, aber trotzdem, wie ich finde, sehr interessant!

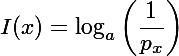
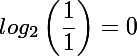










Kommentare (36)